WISE: Whitebox Image Stylization by Example-based Learning

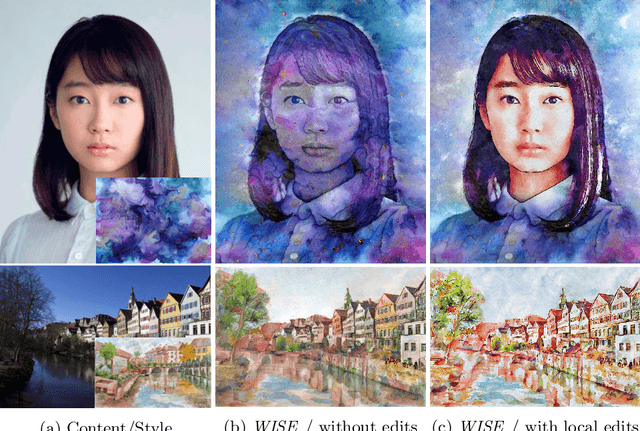
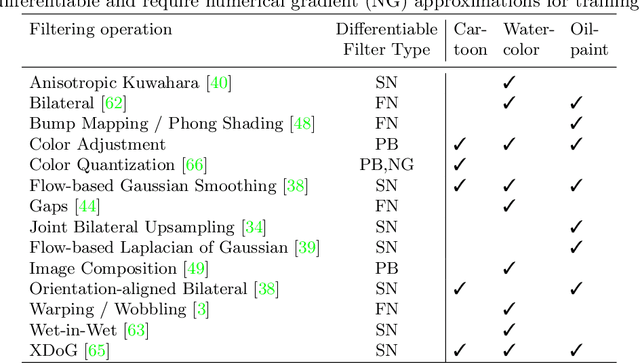
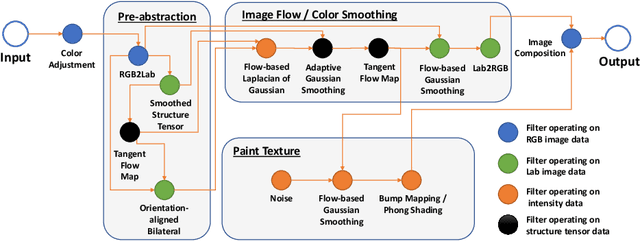
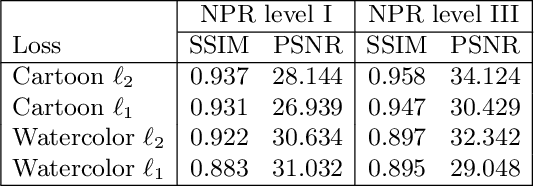
Image-based artistic rendering can synthesize a variety of expressive styles using algorithmic image filtering. In contrast to deep learning-based methods, these heuristics-based filtering techniques can operate on high-resolution images, are interpretable, and can be parameterized according to various design aspects. However, adapting or extending these techniques to produce new styles is often a tedious and error-prone task that requires expert knowledge. We propose a new paradigm to alleviate this problem: implementing algorithmic image filtering techniques as differentiable operations that can learn parametrizations aligned to certain reference styles. To this end, we present WISE, an example-based image-processing system that can handle a multitude of stylization techniques, such as watercolor, oil or cartoon stylization, within a common framework. By training parameter prediction networks for global and local filter parameterizations, we can simultaneously adapt effects to reference styles and image content, e.g., to enhance facial features. Our method can be optimized in a style-transfer framework or learned in a generative-adversarial setting for image-to-image translation. We demonstrate that jointly training an XDoG filter and a CNN for postprocessing can achieve comparable results to a state-of-the-art GAN-based method.

Towards Learning Self-Organized Criticality of Rydberg Atoms using Graph Neural Networks

Self-Organized Criticality (SOC) is a ubiquitous dynamical phenomenon believed to be responsible for the emergence of universal scale-invariant behavior in many, seemingly unrelated systems, such as forest fires, virus spreading or atomic excitation dynamics. SOC describes the buildup of large-scale and long-range spatio-temporal correlations as a result of only local interactions and dissipation. The simulation of SOC dynamics is typically based on Monte-Carlo (MC) methods, which are however numerically expensive and do not scale beyond certain system sizes. We investigate the use of Graph Neural Networks (GNNs) as an effective surrogate model to learn the dynamics operator for a paradigmatic SOC system, inspired by an experimentally accessible physics example: driven Rydberg atoms. To this end, we generalize existing GNN simulation approaches to predict dynamics for the internal state of the node. We show that we can accurately reproduce the MC dynamics as well as generalize along the two important axes of particle number and particle density. This paves the way to model much larger systems beyond the limits of traditional MC methods. While the exact system is inspired by the dynamics of Rydberg atoms, the approach is quite general and can readily be applied to other systems.

Learning the Solution Operator of Boundary Value Problems using Graph Neural Networks

As an alternative to classical numerical solvers for partial differential equations (PDEs) subject to boundary value constraints, there has been a surge of interest in investigating neural networks that can solve such problems efficiently. In this work, we design a general solution operator for two different time-independent PDEs using graph neural networks (GNNs) and spectral graph convolutions. We train the networks on simulated data from a finite elements solver on a variety of shapes and inhomogeneities. In contrast to previous works, we focus on the ability of the trained operator to generalize to previously unseen scenarios. Specifically, we test generalization to meshes with different shapes and superposition of solutions for a different number of inhomogeneities. We find that training on a diverse dataset with lots of variation in the finite element meshes is a key ingredient for achieving good generalization results in all cases. With this, we believe that GNNs can be used to learn solution operators that generalize over a range of properties and produce solutions much faster than a generic solver. Our dataset, which we make publicly available, can be used and extended to verify the robustness of these models under varying conditions.

Maps for Learning Indexable Classes

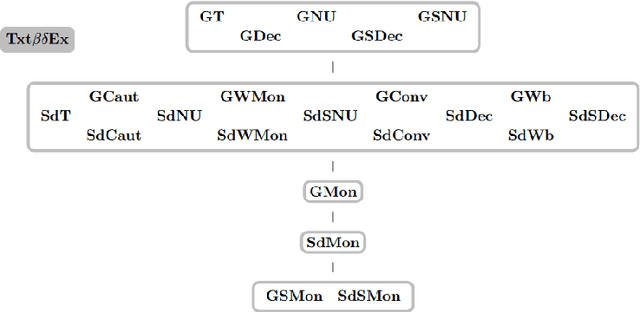
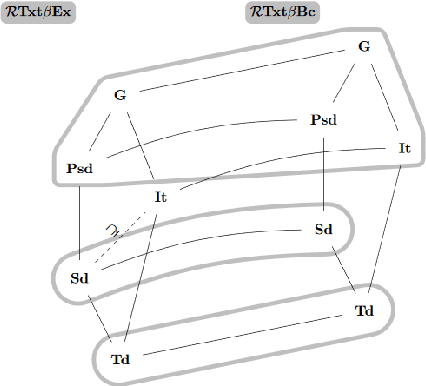
We study learning of indexed families from positive data where a learner can freely choose a hypothesis space (with uniformly decidable membership) comprising at least the languages to be learned. This abstracts a very universal learning task which can be found in many areas, for example learning of (subsets of) regular languages or learning of natural languages. We are interested in various restrictions on learning, such as consistency, conservativeness or set-drivenness, exemplifying various natural learning restrictions. Building on previous results from the literature, we provide several maps (depictions of all pairwise relations) of various groups of learning criteria, including a map for monotonicity restrictions and similar criteria and a map for restrictions on data presentation. Furthermore, we consider, for various learning criteria, whether learners can be assumed consistent.

Using Deep Reinforcement Learning for the Continuous Control of Robotic Arms

Deep reinforcement learning enables algorithms to learn complex behavior, deal with continuous action spaces and find good strategies in environments with high dimensional state spaces. With deep reinforcement learning being an active area of research and many concurrent inventions, we decided to focus on a relatively simple robotic task to evaluate a set of ideas that might help to solve recent reinforcement learning problems. We test a newly created combination of two commonly used reinforcement learning methods, whether it is able to learn more effectively than a baseline. We also compare different ideas to preprocess information before it is fed to the reinforcement learning algorithm. The goal of this strategy is to reduce training time and eventually help the algorithm to converge. The concluding evaluation proves the general applicability of the described concepts by testing them using a simulated environment. These concepts might be reused for future experiments.