Scaling Experiments in Self-Supervised Cross-Table Representation Learning

To analyze the scaling potential of deep tabular representation learning models, we introduce a novel Transformer-based architecture specifically tailored to tabular data and cross-table representation learning by utilizing table-specific tokenizers and a shared Transformer backbone. Our training approach encompasses both single-table and cross-table models, trained via missing value imputation through a self-supervised masked cell recovery objective. To understand the scaling behavior of our method, we train models of varying sizes, ranging from approximately $10^4$ to $10^7$ parameters. These models are trained on a carefully curated pretraining dataset, consisting of 135M training tokens sourced from 76 diverse datasets. We assess the scaling of our architecture in both single-table and cross-table pretraining setups by evaluating the pretrained models using linear probing on a curated set of benchmark datasets and comparing the results with conventional baselines.

Curve Your Enthusiasm: Concurvity Regularization in Differentiable Generalized Additive Models

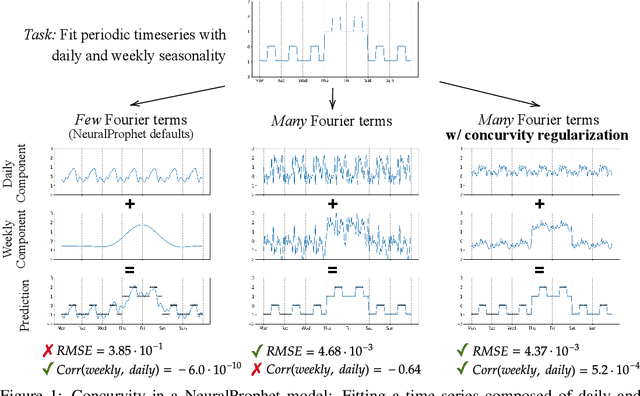
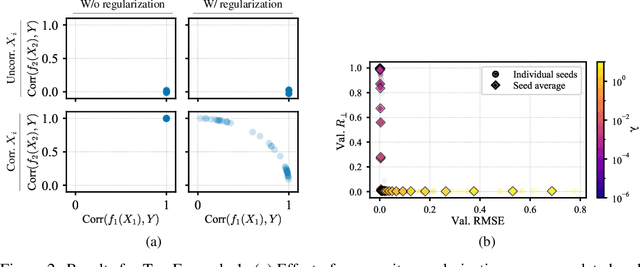
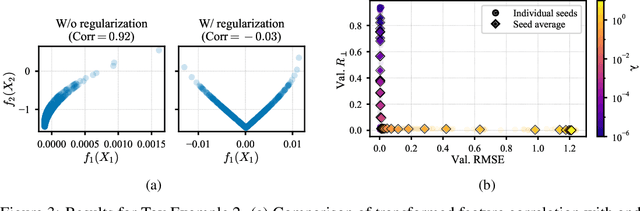
Generalized Additive Models (GAMs) have recently experienced a resurgence in popularity due to their interpretability, which arises from expressing the target value as a sum of non-linear transformations of the features. Despite the current enthusiasm for GAMs, their susceptibility to concurvity - i.e., (possibly non-linear) dependencies between the features - has hitherto been largely overlooked. Here, we demonstrate how concurvity can severly impair the interpretability of GAMs and propose a remedy: a conceptually simple, yet effective regularizer which penalizes pairwise correlations of the non-linearly transformed feature variables. This procedure is applicable to any differentiable additive model, such as Neural Additive Models or NeuralProphet, and enhances interpretability by eliminating ambiguities due to self-canceling feature contributions. We validate the effectiveness of our regularizer in experiments on synthetic as well as real-world datasets for time-series and tabular data. Our experiments show that concurvity in GAMs can be reduced without significantly compromising prediction quality, improving interpretability and reducing variance in the feature importances.

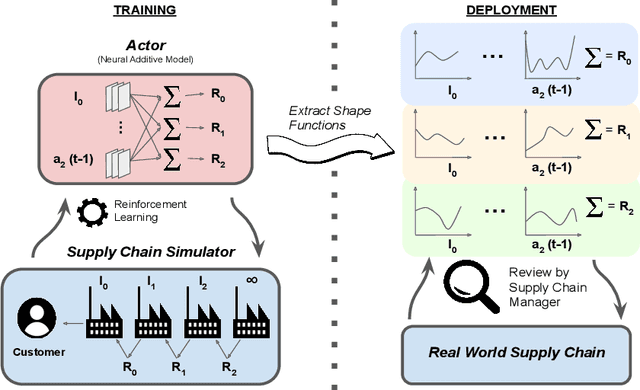
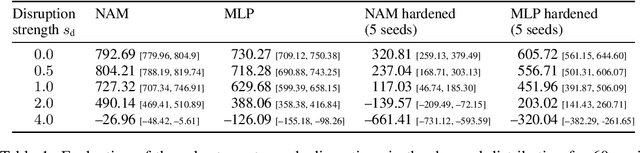
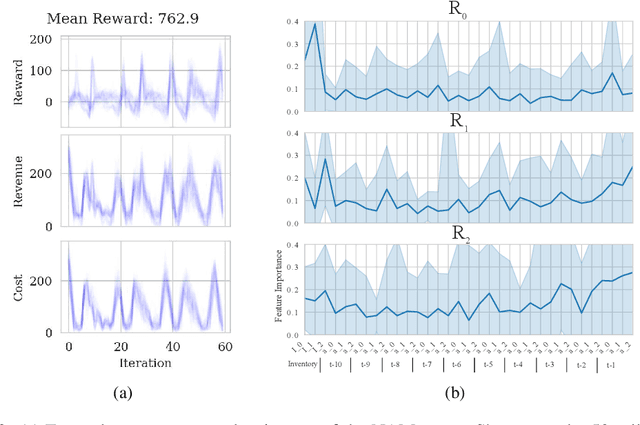
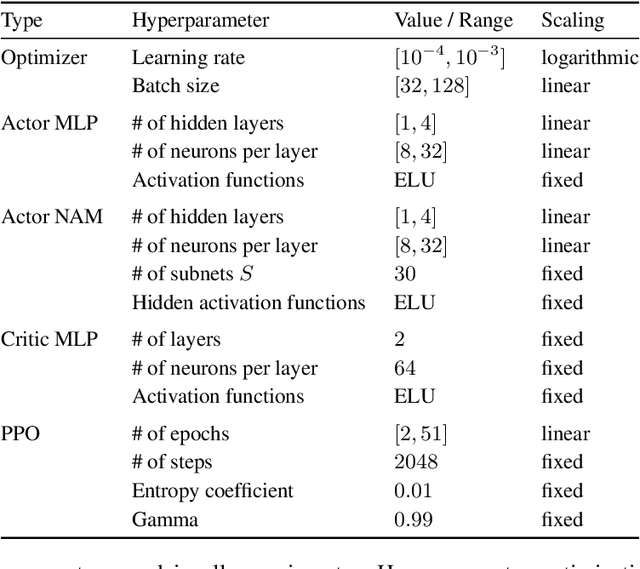
Interpretable Reinforcement Learning via Neural Additive Models for Inventory Management

The COVID-19 pandemic has highlighted the importance of supply chains and the role of digital management to react to dynamic changes in the environment. In this work, we focus on developing dynamic inventory ordering policies for a multi-echelon, i.e. multi-stage, supply chain. Traditional inventory optimization methods aim to determine a static reordering policy. Thus, these policies are not able to adjust to dynamic changes such as those observed during the COVID-19 crisis. On the other hand, conventional strategies offer the advantage of being interpretable, which is a crucial feature for supply chain managers in order to communicate decisions to their stakeholders. To address this limitation, we propose an interpretable reinforcement learning approach that aims to be as interpretable as the traditional static policies while being as flexible and environment-agnostic as other deep learning-based reinforcement learning solutions. We propose to use Neural Additive Models as an interpretable dynamic policy of a reinforcement learning agent, showing that this approach is competitive with a standard full connected policy. Finally, we use the interpretability property to gain insights into a complex ordering strategy for a simple, linear three-echelon inventory supply chain.

Towards Learning Self-Organized Criticality of Rydberg Atoms using Graph Neural Networks

Self-Organized Criticality (SOC) is a ubiquitous dynamical phenomenon believed to be responsible for the emergence of universal scale-invariant behavior in many, seemingly unrelated systems, such as forest fires, virus spreading or atomic excitation dynamics. SOC describes the buildup of large-scale and long-range spatio-temporal correlations as a result of only local interactions and dissipation. The simulation of SOC dynamics is typically based on Monte-Carlo (MC) methods, which are however numerically expensive and do not scale beyond certain system sizes. We investigate the use of Graph Neural Networks (GNNs) as an effective surrogate model to learn the dynamics operator for a paradigmatic SOC system, inspired by an experimentally accessible physics example: driven Rydberg atoms. To this end, we generalize existing GNN simulation approaches to predict dynamics for the internal state of the node. We show that we can accurately reproduce the MC dynamics as well as generalize along the two important axes of particle number and particle density. This paves the way to model much larger systems beyond the limits of traditional MC methods. While the exact system is inspired by the dynamics of Rydberg atoms, the approach is quite general and can readily be applied to other systems.

Learning the Solution Operator of Boundary Value Problems using Graph Neural Networks

As an alternative to classical numerical solvers for partial differential equations (PDEs) subject to boundary value constraints, there has been a surge of interest in investigating neural networks that can solve such problems efficiently. In this work, we design a general solution operator for two different time-independent PDEs using graph neural networks (GNNs) and spectral graph convolutions. We train the networks on simulated data from a finite elements solver on a variety of shapes and inhomogeneities. In contrast to previous works, we focus on the ability of the trained operator to generalize to previously unseen scenarios. Specifically, we test generalization to meshes with different shapes and superposition of solutions for a different number of inhomogeneities. We find that training on a diverse dataset with lots of variation in the finite element meshes is a key ingredient for achieving good generalization results in all cases. With this, we believe that GNNs can be used to learn solution operators that generalize over a range of properties and produce solutions much faster than a generic solver. Our dataset, which we make publicly available, can be used and extended to verify the robustness of these models under varying conditions.

Auto-Compressing Subset Pruning for Semantic Image Segmentation

State-of-the-art semantic segmentation models are characterized by high parameter counts and slow inference times, making them unsuitable for deployment in resource-constrained environments. To address this challenge, we propose \textsc{Auto-Compressing Subset Pruning}, \acosp, as a new online compression method. The core of \acosp consists of learning a channel selection mechanism for individual channels of each convolution in the segmentation model based on an effective temperature annealing schedule. We show a crucial interplay between providing a high-capacity model at the beginning of training and the compression pressure forcing the model to compress concepts into retained channels. We apply \acosp to \segnet and \pspnet architectures and show its success when trained on the \camvid, \city, \voc, and \ade datasets. The results are competitive with existing baselines for compression of segmentation models at low compression ratios and outperform them significantly at high compression ratios, yielding acceptable results even when removing more than $93\%$ of the parameters. In addition, \acosp is conceptually simple, easy to implement, and can readily be generalized to other data modalities, tasks, and architectures. Our code is available at \url{https://github.com/merantix/acosp}.

Optimizing Variational Quantum Circuits using Evolution Strategies

This version withdrawn by arXiv administrators because the submitter did not have the right to agree to our license at the time of submission.