Self-Distilled Representation Learning for Time Series

Self-supervised learning for time-series data holds potential similar to that recently unleashed in Natural Language Processing and Computer Vision. While most existing works in this area focus on contrastive learning, we propose a conceptually simple yet powerful non-contrastive approach, based on the data2vec self-distillation framework. The core of our method is a student-teacher scheme that predicts the latent representation of an input time series from masked views of the same time series. This strategy avoids strong modality-specific assumptions and biases typically introduced by the design of contrastive sample pairs. We demonstrate the competitiveness of our approach for classification and forecasting as downstream tasks, comparing with state-of-the-art self-supervised learning methods on the UCR and UEA archives as well as the ETT and Electricity datasets.

Memorization with neural nets: going beyond the worst case

In practice, deep neural networks are often able to easily interpolate their training data. To understand this phenomenon, many works have aimed to quantify the memorization capacity of a neural network architecture: the largest number of points such that the architecture can interpolate any placement of these points with any assignment of labels. For real-world data, however, one intuitively expects the presence of a benign structure so that interpolation already occurs at a smaller network size than suggested by memorization capacity. In this paper, we investigate interpolation by adopting an instance-specific viewpoint. We introduce a simple randomized algorithm that, given a fixed finite dataset with two classes, with high probability constructs an interpolating three-layer neural network in polynomial time. The required number of parameters is linked to geometric properties of the two classes and their mutual arrangement. As a result, we obtain guarantees that are independent of the number of samples and hence move beyond worst-case memorization capacity bounds. We illustrate the effectiveness of the algorithm in non-pathological situations with extensive numerical experiments and link the insights back to the theoretical results.

Curve Your Enthusiasm: Concurvity Regularization in Differentiable Generalized Additive Models

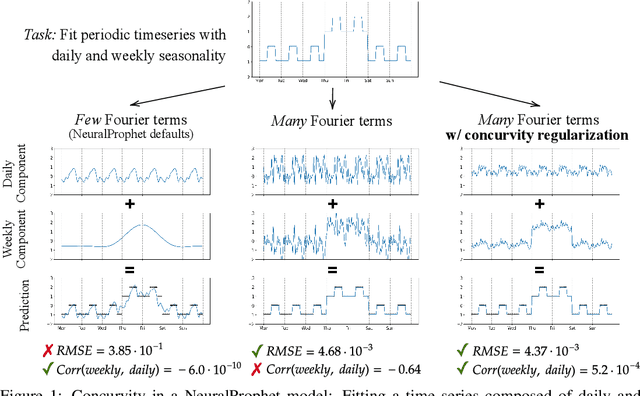
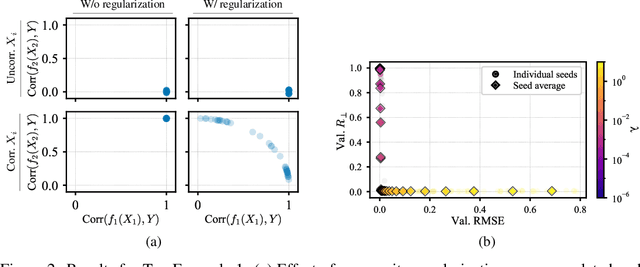
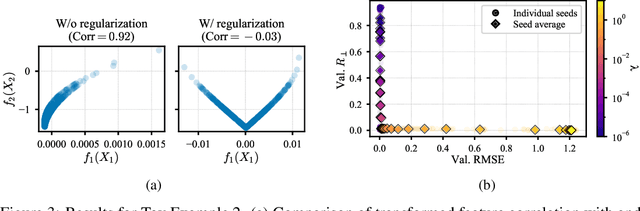
Generalized Additive Models (GAMs) have recently experienced a resurgence in popularity due to their interpretability, which arises from expressing the target value as a sum of non-linear transformations of the features. Despite the current enthusiasm for GAMs, their susceptibility to concurvity - i.e., (possibly non-linear) dependencies between the features - has hitherto been largely overlooked. Here, we demonstrate how concurvity can severly impair the interpretability of GAMs and propose a remedy: a conceptually simple, yet effective regularizer which penalizes pairwise correlations of the non-linearly transformed feature variables. This procedure is applicable to any differentiable additive model, such as Neural Additive Models or NeuralProphet, and enhances interpretability by eliminating ambiguities due to self-canceling feature contributions. We validate the effectiveness of our regularizer in experiments on synthetic as well as real-world datasets for time-series and tabular data. Our experiments show that concurvity in GAMs can be reduced without significantly compromising prediction quality, improving interpretability and reducing variance in the feature importances.

Let's Enhance: A Deep Learning Approach to Extreme Deblurring of Text Images

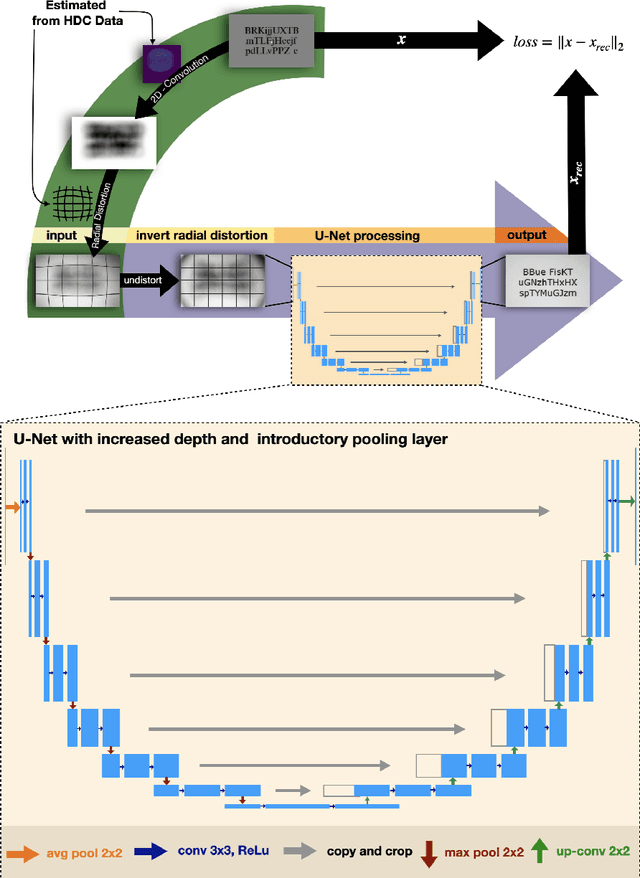
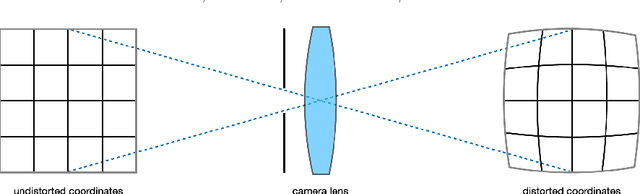
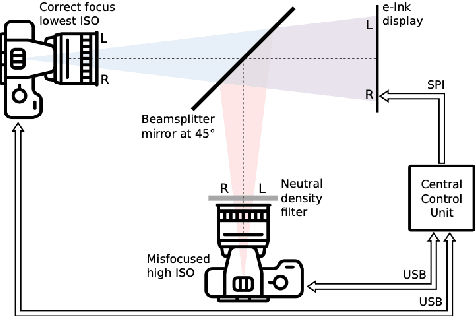
This work presents a novel deep-learning-based pipeline for the inverse problem of image deblurring, leveraging augmentation and pre-training with synthetic data. Our results build on our winning submission to the recent Helsinki Deblur Challenge 2021, whose goal was to explore the limits of state-of-the-art deblurring algorithms in a real-world data setting. The task of the challenge was to deblur out-of-focus images of random text, thereby in a downstream task, maximizing an optical-character-recognition-based score function. A key step of our solution is the data-driven estimation of the physical forward model describing the blur process. This enables a stream of synthetic data, generating pairs of ground-truth and blurry images on-the-fly, which is used for an extensive augmentation of the small amount of challenge data provided. The actual deblurring pipeline consists of an approximate inversion of the radial lens distortion (determined by the estimated forward model) and a U-Net architecture, which is trained end-to-end. Our algorithm was the only one passing the hardest challenge level, achieving over 70% character recognition accuracy. Our findings are well in line with the paradigm of data-centric machine learning, and we demonstrate its effectiveness in the context of inverse problems. Apart from a detailed presentation of our methodology, we also analyze the importance of several design choices in a series of ablation studies. The code of our challenge submission is available under https://github.com/theophil-trippe/HDC_TUBerlin_version_1.

Near-Exact Recovery for Tomographic Inverse Problems via Deep Learning

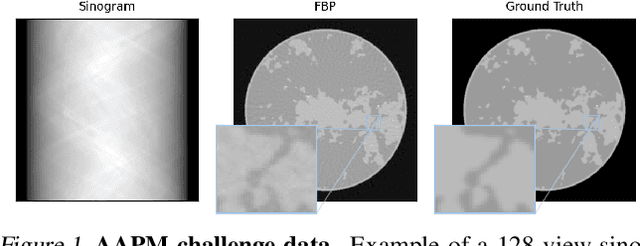
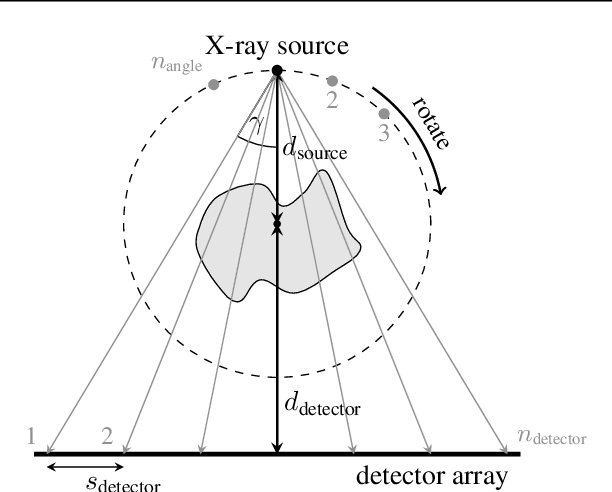
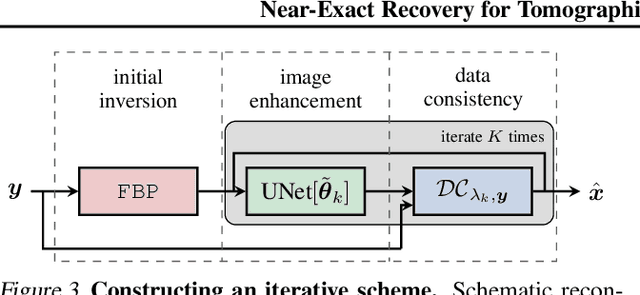
This work is concerned with the following fundamental question in scientific machine learning: Can deep-learning-based methods solve noise-free inverse problems to near-perfect accuracy? Positive evidence is provided for the first time, focusing on a prototypical computed tomography (CT) setup. We demonstrate that an iterative end-to-end network scheme enables reconstructions close to numerical precision, comparable to classical compressed sensing strategies. Our results build on our winning submission to the recent AAPM DL-Sparse-View CT Challenge. Its goal was to identify the state-of-the-art in solving the sparse-view CT inverse problem with data-driven techniques. A specific difficulty of the challenge setup was that the precise forward model remained unknown to the participants. Therefore, a key feature of our approach was to initially estimate the unknown fanbeam geometry in a data-driven calibration step. Apart from an in-depth analysis of our methodology, we also demonstrate its state-of-the-art performance on the open-access real-world dataset LoDoPaB CT.

Gradient-Based Learning of Discrete Structured Measurement Operators for Signal Recovery

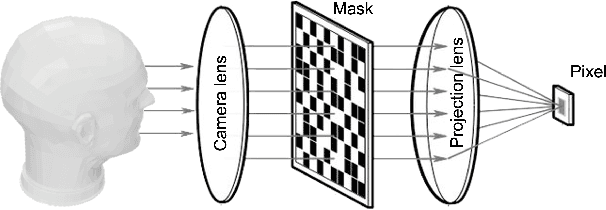
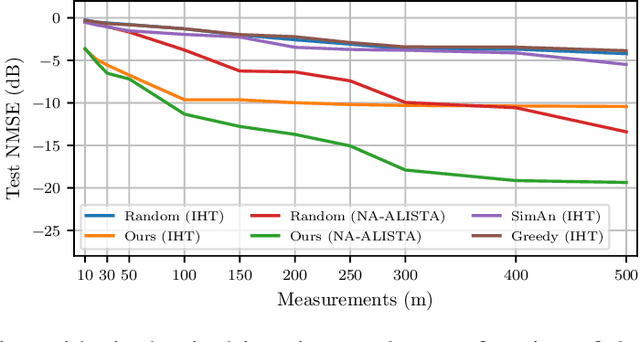
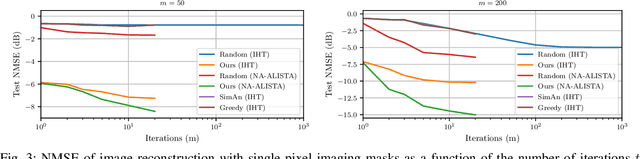
Countless signal processing applications include the reconstruction of signals from few indirect linear measurements. The design of effective measurement operators is typically constrained by the underlying hardware and physics, posing a challenging and often even discrete optimization task. While the potential of gradient-based learning via the unrolling of iterative recovery algorithms has been demonstrated, it has remained unclear how to leverage this technique when the set of admissible measurement operators is structured and discrete. We tackle this problem by combining unrolled optimization with Gumbel reparametrizations, which enable the computation of low-variance gradient estimates of categorical random variables. Our approach is formalized by GLODISMO (Gradient-based Learning of DIscrete Structured Measurement Operators). This novel method is easy-to-implement, computationally efficient, and extendable due to its compatibility with automatic differentiation. We empirically demonstrate the performance and flexibility of GLODISMO in several prototypical signal recovery applications, verifying that the learned measurement matrices outperform conventional designs based on randomization as well as discrete optimization baselines.

The Separation Capacity of Random Neural Networks

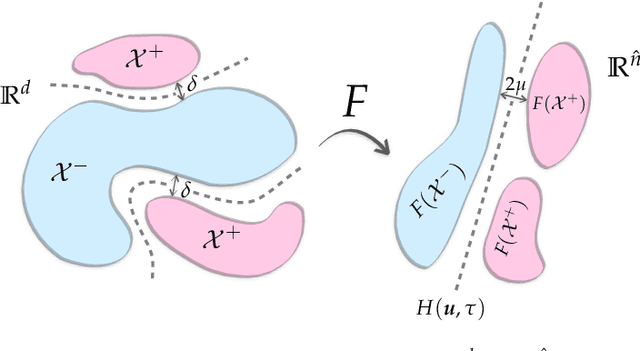
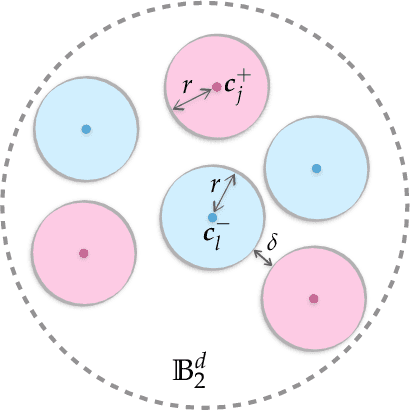
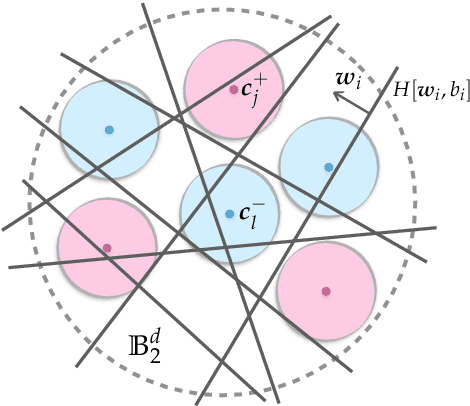
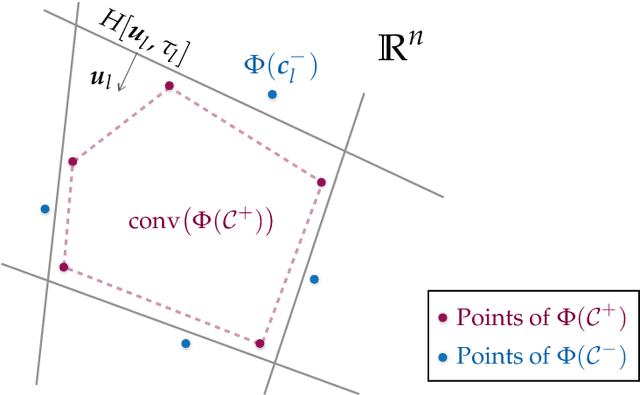
Neural networks with random weights appear in a variety of machine learning applications, most prominently as the initialization of many deep learning algorithms and as a computationally cheap alternative to fully learned neural networks. In the present article we enhance the theoretical understanding of random neural nets by addressing the following data separation problem: under what conditions can a random neural network make two classes $\mathcal{X}^-, \mathcal{X}^+ \subset \mathbb{R}^d$ (with positive distance) linearly separable? We show that a sufficiently large two-layer ReLU-network with standard Gaussian weights and uniformly distributed biases can solve this problem with high probability. Crucially, the number of required neurons is explicitly linked to geometric properties of the underlying sets $\mathcal{X}^-, \mathcal{X}^+$ and their mutual arrangement. This instance-specific viewpoint allows us to overcome the usual curse of dimensionality (exponential width of the layers) in non-pathological situations where the data carries low-complexity structure. We quantify the relevant structure of the data in terms of a novel notion of mutual complexity (based on a localized version of Gaussian mean width), which leads to sound and informative separation guarantees. We connect our result with related lines of work on approximation, memorization, and generalization.

AAPM DL-Sparse-View CT Challenge Submission Report: Designing an Iterative Network for Fanbeam-CT with Unknown Geometry

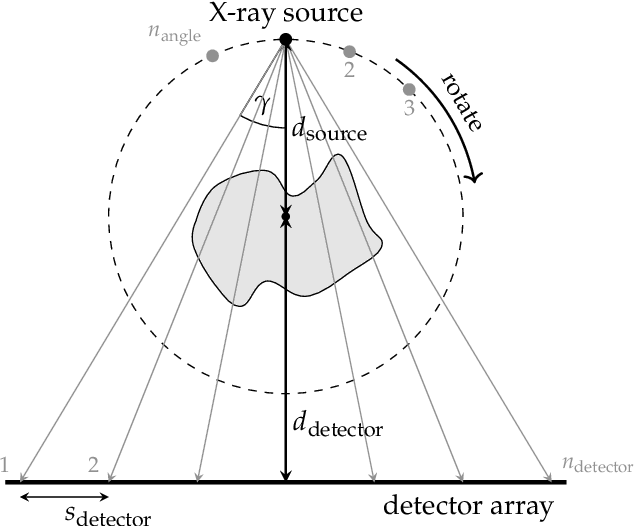
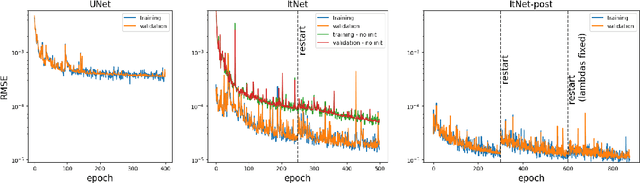
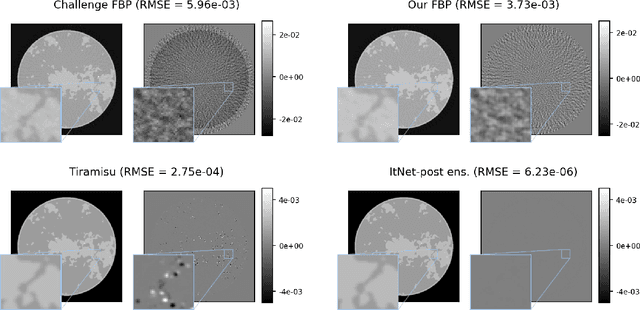
This report is dedicated to a short motivation and description of our contribution to the AAPM DL-Sparse-View CT Challenge (team name: "robust-and-stable"). The task is to recover breast model phantom images from limited view fanbeam measurements using data-driven reconstruction techniques. The challenge is distinctive in the sense that participants are provided with a collection of ground truth images and their noiseless, subsampled sinograms (as well as the associated limited view filtered backprojection images), but not with the actual forward model. Therefore, our approach first estimates the fanbeam geometry in a data-driven geometric calibration step. In a subsequent two-step procedure, we design an iterative end-to-end network that enables the computation of near-exact solutions.

Solving Inverse Problems With Deep Neural Networks -- Robustness Included?

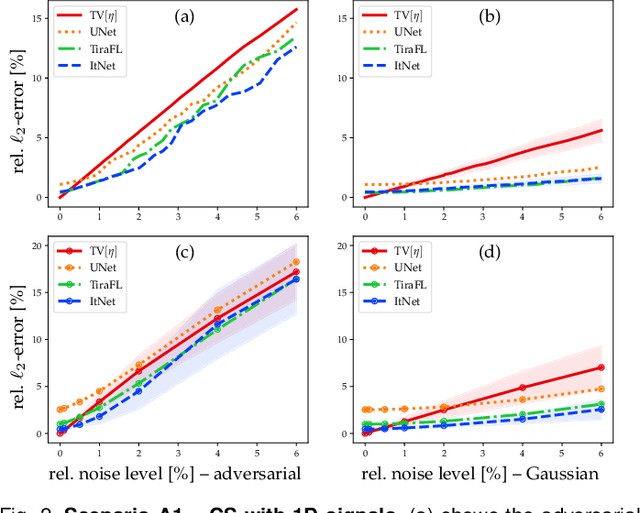
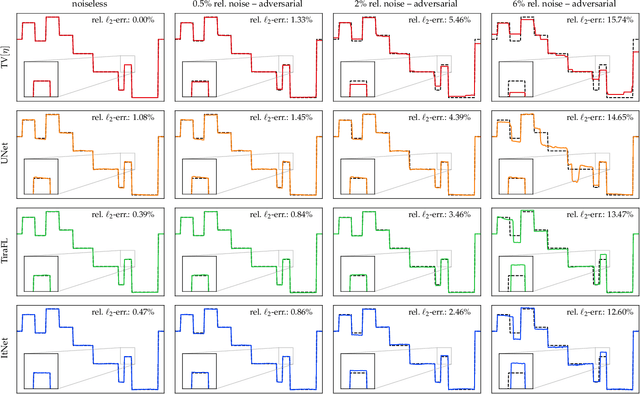
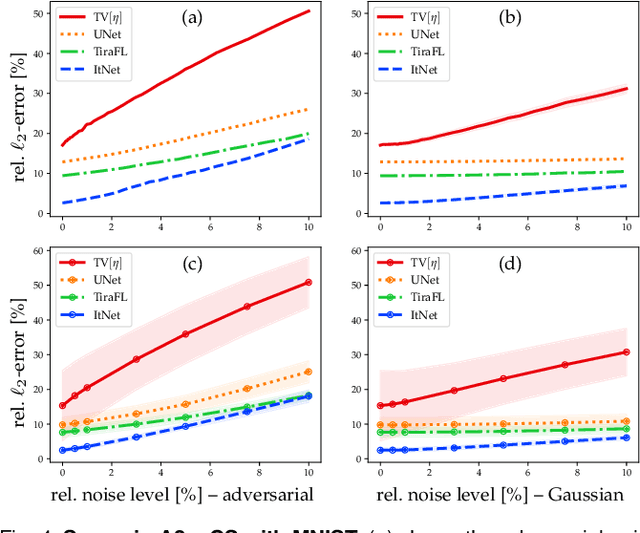
In the past five years, deep learning methods have become state-of-the-art in solving various inverse problems. Before such approaches can find application in safety-critical fields, a verification of their reliability appears mandatory. Recent works have pointed out instabilities of deep neural networks for several image reconstruction tasks. In analogy to adversarial attacks in classification, it was shown that slight distortions in the input domain may cause severe artifacts. The present article sheds new light on this concern, by conducting an extensive study of the robustness of deep-learning-based algorithms for solving underdetermined inverse problems. This covers compressed sensing with Gaussian measurements as well as image recovery from Fourier and Radon measurements, including a real-world scenario for magnetic resonance imaging (using the NYU-fastMRI dataset). Our main focus is on computing adversarial perturbations of the measurements that maximize the reconstruction error. A distinctive feature of our approach is the quantitative and qualitative comparison with total-variation minimization, which serves as a provably robust reference method. In contrast to previous findings, our results reveal that standard end-to-end network architectures are not only resilient against statistical noise, but also against adversarial perturbations. All considered networks are trained by common deep learning techniques, without sophisticated defense strategies.

Generic Error Bounds for the Generalized Lasso with Sub-Exponential Data

This work performs a non-asymptotic analysis of the generalized Lasso under the assumption of sub-exponential data. Our main results continue recent research on the benchmark case of (sub-)Gaussian sample distributions and thereby explore what conclusions are still valid when going beyond. While many statistical features of the generalized Lasso remain unaffected (e.g., consistency), the key difference becomes manifested in the way how the complexity of the hypothesis set is measured. It turns out that the estimation error can be controlled by means of two complexity parameters that arise naturally from a generic-chaining-based proof strategy. The output model can be non-realizable, while the only requirement for the input vector is a generic concentration inequality of Bernstein-type, which can be implemented for a variety of sub-exponential distributions. This abstract approach allows us to reproduce, unify, and extend previously known guarantees for the generalized Lasso. In particular, we present applications to semi-parametric output models and phase retrieval via the lifted Lasso. Moreover, our findings are discussed in the context of sparse recovery and high-dimensional estimation problems.