Float8@2bits: Entropy Coding Enables Data-Free Model Compression

Post-training compression is currently divided into two contrasting regimes. On the one hand, fast, data-free, and model-agnostic methods (e.g., NF4 or HQQ) offer maximum accessibility but suffer from functional collapse at extreme bit-rates below 4 bits. On the other hand, techniques leveraging calibration data or extensive recovery training achieve superior fidelity but impose high computational constraints and face uncertain robustness under data distribution shifts. We introduce EntQuant, the first framework to unite the advantages of these distinct paradigms. By matching the performance of data-dependent methods with the speed and universality of data-free techniques, EntQuant enables practical utility in the extreme compression regime. Our method decouples numerical precision from storage cost via entropy coding, compressing a 70B parameter model in less than 30 minutes. We demonstrate that EntQuant does not only achieve state-of-the-art results on standard evaluation sets and models, but also retains functional performance on more complex benchmarks with instruction-tuned models, all at modest inference overhead.

Choose Your Model Size: Any Compression by a Single Gradient Descent

The adoption of Foundation Models in resource-constrained environments remains challenging due to their large size and inference costs. A promising way to overcome these limitations is post-training compression, which aims to balance reduced model size against performance degradation. This work presents Any Compression via Iterative Pruning (ACIP), a novel algorithmic approach to determine a compression-performance trade-off from a single stochastic gradient descent run. To ensure parameter efficiency, we use an SVD-reparametrization of linear layers and iteratively prune their singular values with a sparsity-inducing penalty. The resulting pruning order gives rise to a global parameter ranking that allows us to materialize models of any target size. Importantly, the compressed models exhibit strong predictive downstream performance without the need for costly fine-tuning. We evaluate ACIP on a large selection of open-weight LLMs and tasks, and demonstrate state-of-the-art results compared to existing factorisation-based compression methods. We also show that ACIP seamlessly complements common quantization-based compression techniques.

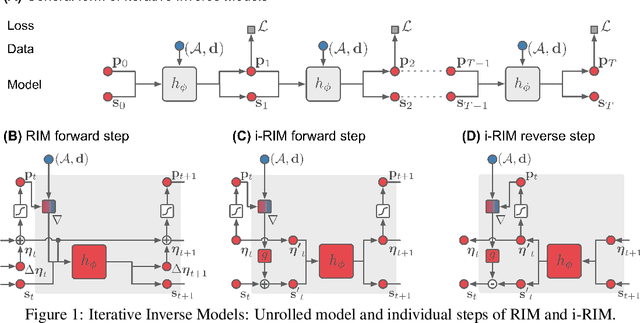
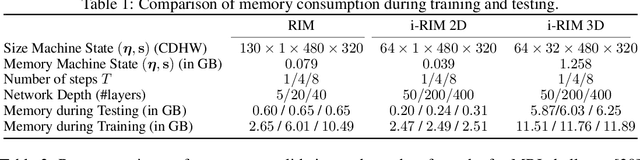
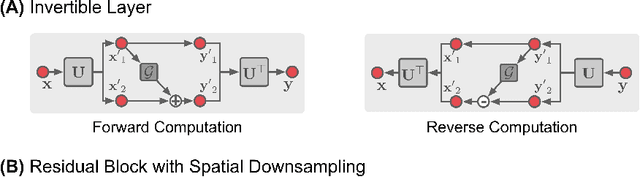
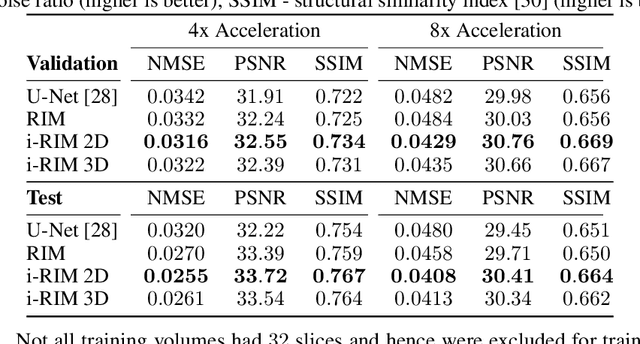
Invert to Learn to Invert

Iterative learning to infer approaches have become popular solvers for inverse problems. However, their memory requirements during training grow linearly with model depth, limiting in practice model expressiveness. In this work, we propose an iterative inverse model with constant memory that relies on invertible networks to avoid storing intermediate activations. As a result, the proposed approach allows us to train models with 400 layers on 3D volumes in an MRI image reconstruction task. In experiments on a public data set, we demonstrate that these deeper, and thus more expressive, networks perform state-of-the-art image reconstruction.

i-RIM applied to the fastMRI challenge

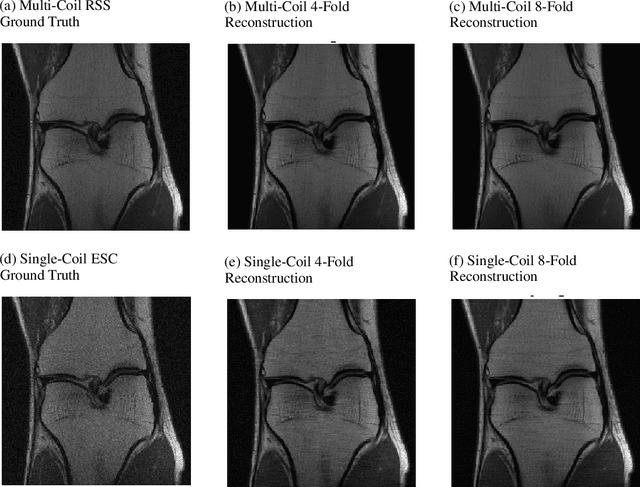
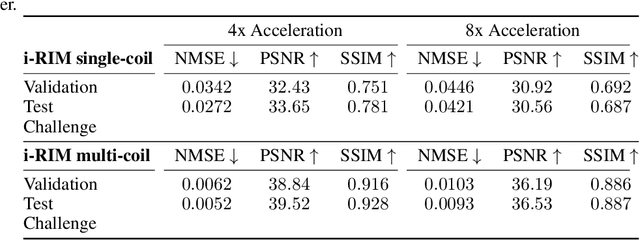
We, team AImsterdam, summarize our submission to the fastMRI challenge (Zbontar et al., 2018). Our approach builds on recent advances in invertible learning to infer models as presented in Putzky and Welling (2019). Both, our single-coil and our multi-coil model share the same basic architecture.

Recurrent Inference Machines for Solving Inverse Problems

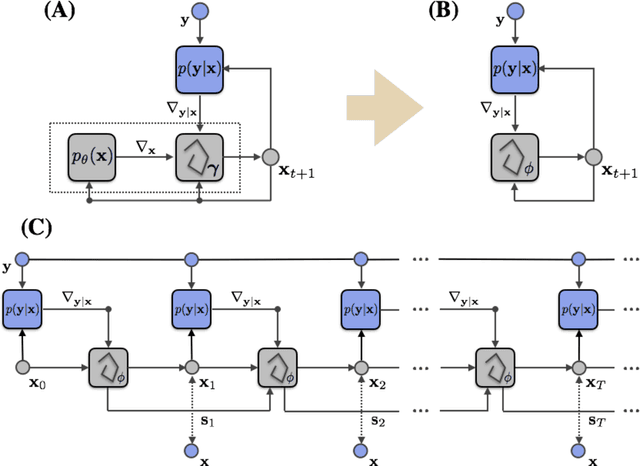
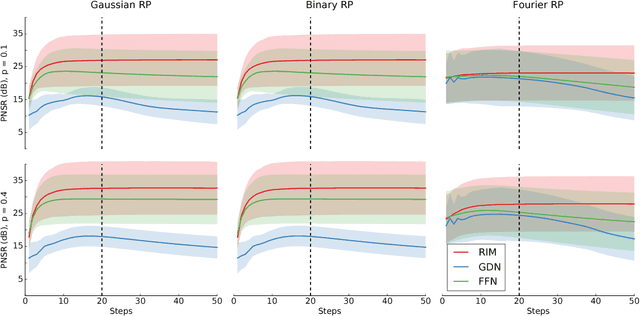
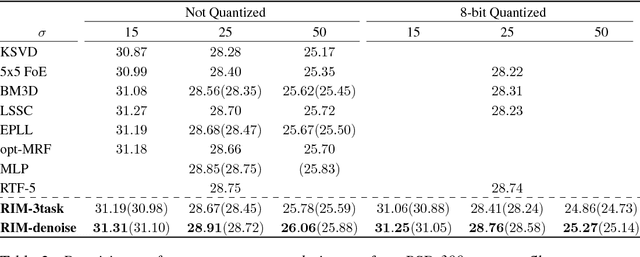
Much of the recent research on solving iterative inference problems focuses on moving away from hand-chosen inference algorithms and towards learned inference. In the latter, the inference process is unrolled in time and interpreted as a recurrent neural network (RNN) which allows for joint learning of model and inference parameters with back-propagation through time. In this framework, the RNN architecture is directly derived from a hand-chosen inference algorithm, effectively limiting its capabilities. We propose a learning framework, called Recurrent Inference Machines (RIM), in which we turn algorithm construction the other way round: Given data and a task, train an RNN to learn an inference algorithm. Because RNNs are Turing complete [1, 2] they are capable to implement any inference algorithm. The framework allows for an abstraction which removes the need for domain knowledge. We demonstrate in several image restoration experiments that this abstraction is effective, allowing us to achieve state-of-the-art performance on image denoising and super-resolution tasks and superior across-task generalization.