Learning Hamiltonian Flow Maps: Mean Flow Consistency for Large-Timestep Molecular Dynamics

Simulating the long-time evolution of Hamiltonian systems is limited by the small timesteps required for stable numerical integration. To overcome this constraint, we introduce a framework to learn Hamiltonian Flow Maps by predicting the mean phase-space evolution over a chosen time span $Δt$, enabling stable large-timestep updates far beyond the stability limits of classical integrators. To this end, we impose a Mean Flow consistency condition for time-averaged Hamiltonian dynamics. Unlike prior approaches, this allows training on independent phase-space samples without access to future states, avoiding expensive trajectory generation. Validated across diverse Hamiltonian systems, our method in particular improves upon molecular dynamics simulations using machine-learned force fields (MLFF). Our models maintain comparable training and inference cost, but support significantly larger integration timesteps while trained directly on widely-available trajectory-free MLFF datasets.

Sampling 3D Molecular Conformers with Diffusion Transformers

Diffusion Transformers (DiTs) have demonstrated strong performance in generative modeling, particularly in image synthesis, making them a compelling choice for molecular conformer generation. However, applying DiTs to molecules introduces novel challenges, such as integrating discrete molecular graph information with continuous 3D geometry, handling Euclidean symmetries, and designing conditioning mechanisms that generalize across molecules of varying sizes and structures. We propose DiTMC, a framework that adapts DiTs to address these challenges through a modular architecture that separates the processing of 3D coordinates from conditioning on atomic connectivity. To this end, we introduce two complementary graph-based conditioning strategies that integrate seamlessly with the DiT architecture. These are combined with different attention mechanisms, including both standard non-equivariant and SO(3)-equivariant formulations, enabling flexible control over the trade-off between between accuracy and computational efficiency. Experiments on standard conformer generation benchmarks (GEOM-QM9, -DRUGS, -XL) demonstrate that DiTMC achieves state-of-the-art precision and physical validity. Our results highlight how architectural choices and symmetry priors affect sample quality and efficiency, suggesting promising directions for large-scale generative modeling of molecular structures. Code available at https://github.com/ML4MolSim/dit_mc.

Enhancing Diffusion Models Efficiency by Disentangling Total-Variance and Signal-to-Noise Ratio

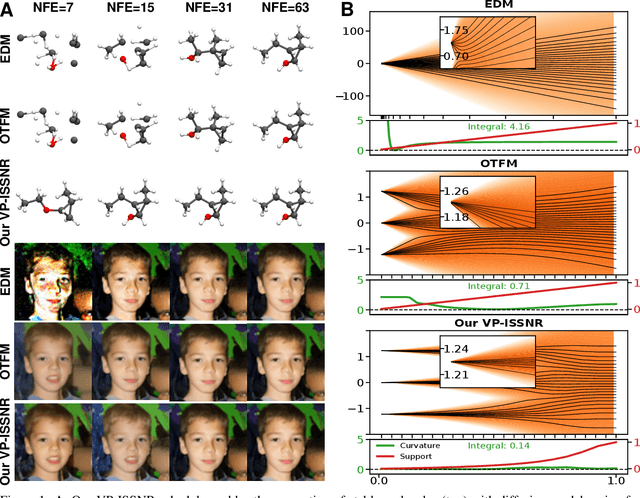
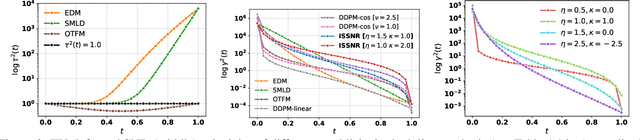
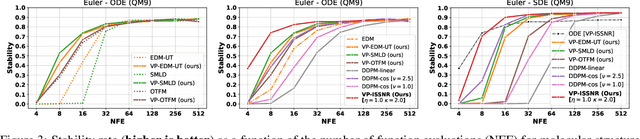
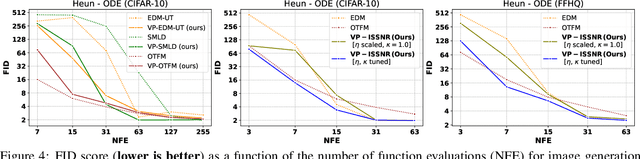
The long sampling time of diffusion models remains a significant bottleneck, which can be mitigated by reducing the number of diffusion time steps. However, the quality of samples with fewer steps is highly dependent on the noise schedule, i.e., the specific manner in which noise is introduced and the signal is reduced at each step. Although prior work has improved upon the original variance-preserving and variance-exploding schedules, these approaches $\textit{passively}$ adjust the total variance, without direct control over it. In this work, we propose a novel total-variance/signal-to-noise-ratio disentangled (TV/SNR) framework, where TV and SNR can be controlled independently. Our approach reveals that different existing schedules, where the TV explodes exponentially, can be $\textit{improved}$ by setting a constant TV schedule while preserving the same SNR schedule. Furthermore, generalizing the SNR schedule of the optimal transport flow matching significantly improves the performance in molecular structure generation, achieving few step generation of stable molecules. A similar tendency is observed in image generation, where our approach with a uniform diffusion time grid performs comparably to the highly tailored EDM sampler.

Multiscale Neural Operators for Solving Time-Independent PDEs

Time-independent Partial Differential Equations (PDEs) on large meshes pose significant challenges for data-driven neural PDE solvers. We introduce a novel graph rewiring technique to tackle some of these challenges, such as aggregating information across scales and on irregular meshes. Our proposed approach bridges distant nodes, enhancing the global interaction capabilities of GNNs. Our experiments on three datasets reveal that GNN-based methods set new performance standards for time-independent PDEs on irregular meshes. Finally, we show that our graph rewiring strategy boosts the performance of baseline methods, achieving state-of-the-art results in one of the tasks.

Enhancing Multi-Objective Optimization through Machine Learning-Supported Multiphysics Simulation

Multiphysics simulations that involve multiple coupled physical phenomena quickly become computationally expensive. This imposes challenges for practitioners aiming to find optimal configurations for these problems satisfying multiple objectives, as optimization algorithms often require querying the simulation many times. This paper presents a methodological framework for training, self-optimizing, and self-organizing surrogate models to approximate and speed up Multiphysics simulations. We generate two real-world tabular datasets, which we make publicly available, and show that surrogate models can be trained on relatively small amounts of data to approximate the underlying simulations accurately. We conduct extensive experiments combining four machine learning and deep learning algorithms with two optimization algorithms and a comprehensive evaluation strategy. Finally, we evaluate the performance of our combined training and optimization pipeline by verifying the generated Pareto-optimal results using the ground truth simulations. We also employ explainable AI techniques to analyse our surrogates and conduct a preselection strategy to determine the most relevant features in our real-world examples. This approach lets us understand the underlying problem and identify critical partial dependencies.

Curve Your Enthusiasm: Concurvity Regularization in Differentiable Generalized Additive Models

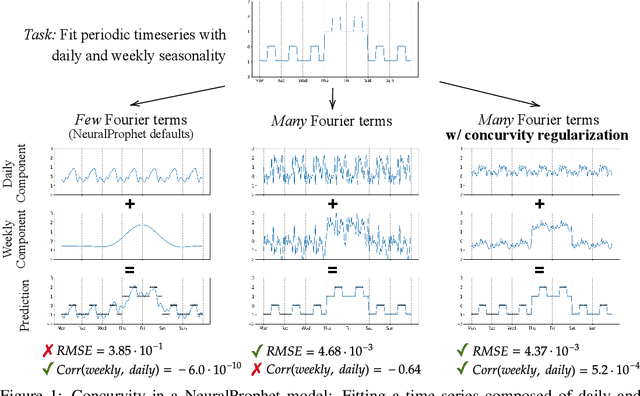
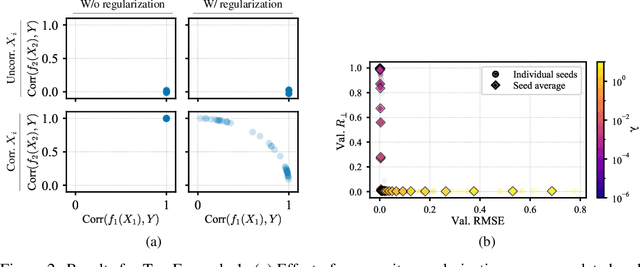
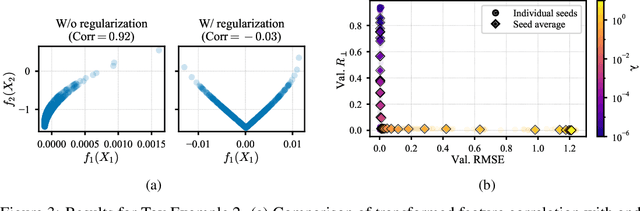
Generalized Additive Models (GAMs) have recently experienced a resurgence in popularity due to their interpretability, which arises from expressing the target value as a sum of non-linear transformations of the features. Despite the current enthusiasm for GAMs, their susceptibility to concurvity - i.e., (possibly non-linear) dependencies between the features - has hitherto been largely overlooked. Here, we demonstrate how concurvity can severly impair the interpretability of GAMs and propose a remedy: a conceptually simple, yet effective regularizer which penalizes pairwise correlations of the non-linearly transformed feature variables. This procedure is applicable to any differentiable additive model, such as Neural Additive Models or NeuralProphet, and enhances interpretability by eliminating ambiguities due to self-canceling feature contributions. We validate the effectiveness of our regularizer in experiments on synthetic as well as real-world datasets for time-series and tabular data. Our experiments show that concurvity in GAMs can be reduced without significantly compromising prediction quality, improving interpretability and reducing variance in the feature importances.