Characterizing High-Capacity Janus Aminobenzene-Graphene Anode for Sodium-Ion Batteries with Machine Learning

Sodium-ion batteries require anodes that combine high capacity, low operating voltage, fast Na-ion transport, and mechanical stability, which conventional anodes struggle to deliver. Here, we use the SpookyNet machine-learning force field (MLFF) together with all-electron density-functional theory calculations to characterize Na storage in aminobenzene-functionalized Janus graphene (Na$_x$AB) at room-temperature. Simulations across state of charge reveal a three-stage storage mechanism-site-specific adsorption at aminobenzene groups and Na$_n$@AB$_m$ structure formation, followed by interlayer gallery filling-contrasting the multi-stage pore-, graphite-interlayer-, and defect-controlled behavior in hard carbon. This leads to an OCV profile with an extended low-voltage plateau of 0.15 V vs. Na/Na$^{+}$, an estimated gravimetric capacity of $\sim$400 mAh g$^{-1}$, negligible volume change, and Na diffusivities of $\sim10^{-6}$ cm$^{2}$ s$^{-1}$, two to three orders of magnitude higher than in hard carbon. Our results establish Janus aminobenzene-graphene as a promising, structurally defined high-capacity Na-ion anode and illustrate the power of MLFF-based simulations for characterizing electrode materials.

Learning Hamiltonian Flow Maps: Mean Flow Consistency for Large-Timestep Molecular Dynamics

Simulating the long-time evolution of Hamiltonian systems is limited by the small timesteps required for stable numerical integration. To overcome this constraint, we introduce a framework to learn Hamiltonian Flow Maps by predicting the mean phase-space evolution over a chosen time span $Δt$, enabling stable large-timestep updates far beyond the stability limits of classical integrators. To this end, we impose a Mean Flow consistency condition for time-averaged Hamiltonian dynamics. Unlike prior approaches, this allows training on independent phase-space samples without access to future states, avoiding expensive trajectory generation. Validated across diverse Hamiltonian systems, our method in particular improves upon molecular dynamics simulations using machine-learned force fields (MLFF). Our models maintain comparable training and inference cost, but support significantly larger integration timesteps while trained directly on widely-available trajectory-free MLFF datasets.

Control Variate Score Matching for Diffusion Models

Diffusion models offer a robust framework for sampling from unnormalized probability densities, which requires accurately estimating the score of the noise-perturbed target distribution. While the standard Denoising Score Identity (DSI) relies on data samples, access to the target energy function enables an alternative formulation via the Target Score Identity (TSI). However, these estimators face a fundamental variance trade-off: DSI exhibits high variance in low-noise regimes, whereas TSI suffers from high variance at high noise levels. In this work, we reconcile these approaches by unifying both estimators within the principled framework of control variates. We introduce the Control Variate Score Identity (CVSI), deriving an optimal, time-dependent control coefficient that theoretically guarantees variance minimization across the entire noise spectrum. We demonstrate that CVSI serves as a robust, low-variance plug-in estimator that significantly enhances sample efficiency in both data-free sampler learning and inference-time diffusion sampling.

Sampling 3D Molecular Conformers with Diffusion Transformers

Diffusion Transformers (DiTs) have demonstrated strong performance in generative modeling, particularly in image synthesis, making them a compelling choice for molecular conformer generation. However, applying DiTs to molecules introduces novel challenges, such as integrating discrete molecular graph information with continuous 3D geometry, handling Euclidean symmetries, and designing conditioning mechanisms that generalize across molecules of varying sizes and structures. We propose DiTMC, a framework that adapts DiTs to address these challenges through a modular architecture that separates the processing of 3D coordinates from conditioning on atomic connectivity. To this end, we introduce two complementary graph-based conditioning strategies that integrate seamlessly with the DiT architecture. These are combined with different attention mechanisms, including both standard non-equivariant and SO(3)-equivariant formulations, enabling flexible control over the trade-off between between accuracy and computational efficiency. Experiments on standard conformer generation benchmarks (GEOM-QM9, -DRUGS, -XL) demonstrate that DiTMC achieves state-of-the-art precision and physical validity. Our results highlight how architectural choices and symmetry priors affect sample quality and efficiency, suggesting promising directions for large-scale generative modeling of molecular structures. Code available at https://github.com/ML4MolSim/dit_mc.

How simple can you go? An off-the-shelf transformer approach to molecular dynamics

Most current neural networks for molecular dynamics (MD) include physical inductive biases, resulting in specialized and complex architectures. This is in contrast to most other machine learning domains, where specialist approaches are increasingly replaced by general-purpose architectures trained on vast datasets. In line with this trend, several recent studies have questioned the necessity of architectural features commonly found in MD models, such as built-in rotational equivariance or energy conservation. In this work, we contribute to the ongoing discussion by evaluating the performance of an MD model with as few specialized architectural features as possible. We present a recipe for MD using an Edge Transformer, an "off-the-shelf'' transformer architecture that has been minimally modified for the MD domain, termed MD-ET. Our model implements neither built-in equivariance nor energy conservation. We use a simple supervised pre-training scheme on $\sim$30 million molecular structures from the QCML database. Using this "off-the-shelf'' approach, we show state-of-the-art results on several benchmarks after fine-tuning for a small number of steps. Additionally, we examine the effects of being only approximately equivariant and energy conserving for MD simulations, proposing a novel method for distinguishing the errors resulting from non-equivariance from other sources of inaccuracies like numerical rounding errors. While our model exhibits runaway energy increases on larger structures, we show approximately energy-conserving NVE simulations for a range of small structures.

Enhancing Diffusion Models Efficiency by Disentangling Total-Variance and Signal-to-Noise Ratio

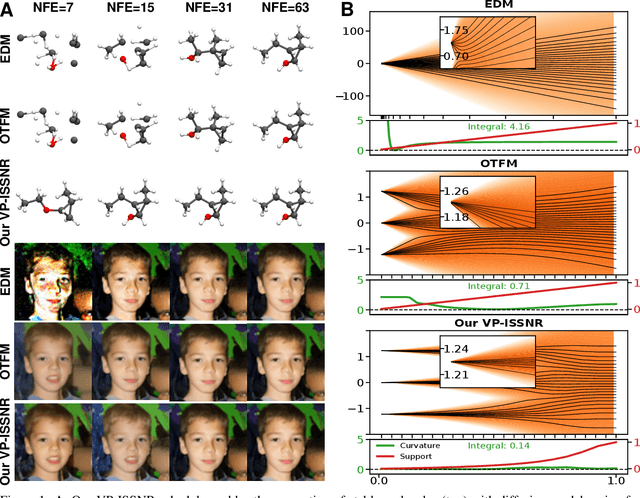
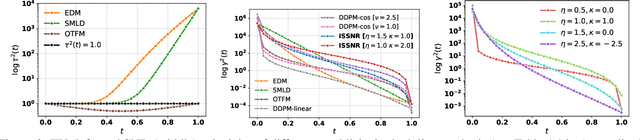
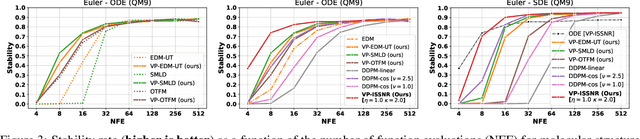
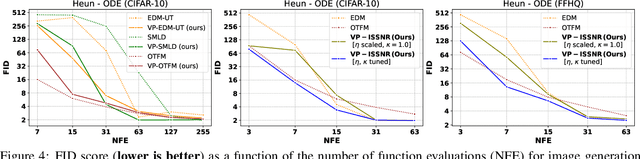
The long sampling time of diffusion models remains a significant bottleneck, which can be mitigated by reducing the number of diffusion time steps. However, the quality of samples with fewer steps is highly dependent on the noise schedule, i.e., the specific manner in which noise is introduced and the signal is reduced at each step. Although prior work has improved upon the original variance-preserving and variance-exploding schedules, these approaches $\textit{passively}$ adjust the total variance, without direct control over it. In this work, we propose a novel total-variance/signal-to-noise-ratio disentangled (TV/SNR) framework, where TV and SNR can be controlled independently. Our approach reveals that different existing schedules, where the TV explodes exponentially, can be $\textit{improved}$ by setting a constant TV schedule while preserving the same SNR schedule. Furthermore, generalizing the SNR schedule of the optimal transport flow matching significantly improves the performance in molecular structure generation, achieving few step generation of stable molecules. A similar tendency is observed in image generation, where our approach with a uniform diffusion time grid performs comparably to the highly tailored EDM sampler.

Euclidean Fast Attention: Machine Learning Global Atomic Representations at Linear Cost

Long-range correlations are essential across numerous machine learning tasks, especially for data embedded in Euclidean space, where the relative positions and orientations of distant components are often critical for accurate predictions. Self-attention offers a compelling mechanism for capturing these global effects, but its quadratic complexity presents a significant practical limitation. This problem is particularly pronounced in computational chemistry, where the stringent efficiency requirements of machine learning force fields (MLFFs) often preclude accurately modeling long-range interactions. To address this, we introduce Euclidean fast attention (EFA), a linear-scaling attention-like mechanism designed for Euclidean data, which can be easily incorporated into existing model architectures. A core component of EFA are novel Euclidean rotary positional encodings (ERoPE), which enable efficient encoding of spatial information while respecting essential physical symmetries. We empirically demonstrate that EFA effectively captures diverse long-range effects, enabling EFA-equipped MLFFs to describe challenging chemical interactions for which conventional MLFFs yield incorrect results.

Complete and Efficient Covariants for 3D Point Configurations with Application to Learning Molecular Quantum Properties

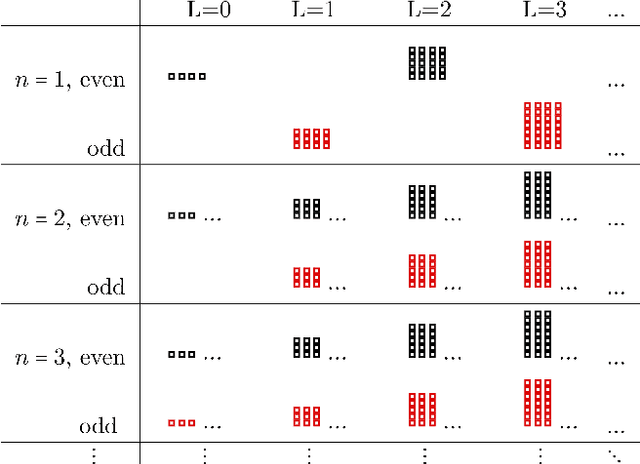
When modeling physical properties of molecules with machine learning, it is desirable to incorporate $SO(3)$-covariance. While such models based on low body order features are not complete, we formulate and prove general completeness properties for higher order methods, and show that $6k-5$ of these features are enough for up to $k$ atoms. We also find that the Clebsch--Gordan operations commonly used in these methods can be replaced by matrix multiplications without sacrificing completeness, lowering the scaling from $O(l^6)$ to $O(l^3)$ in the degree of the features. We apply this to quantum chemistry, but the proposed methods are generally applicable for problems involving 3D point configurations.

E3x: $\mathrm{E}$-Equivariant Deep Learning Made Easy

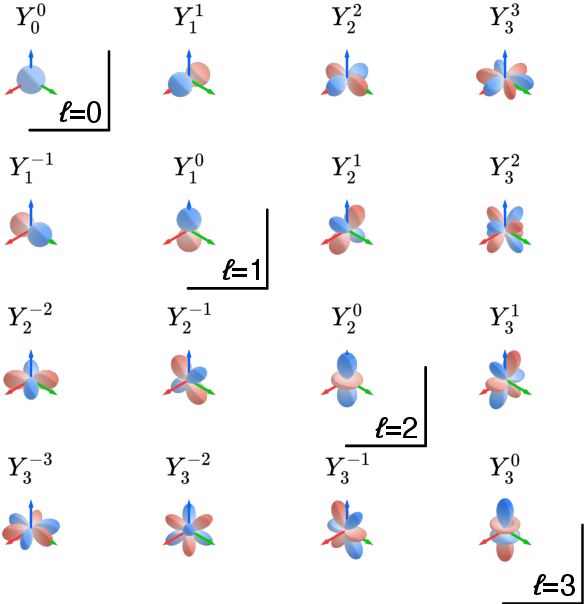
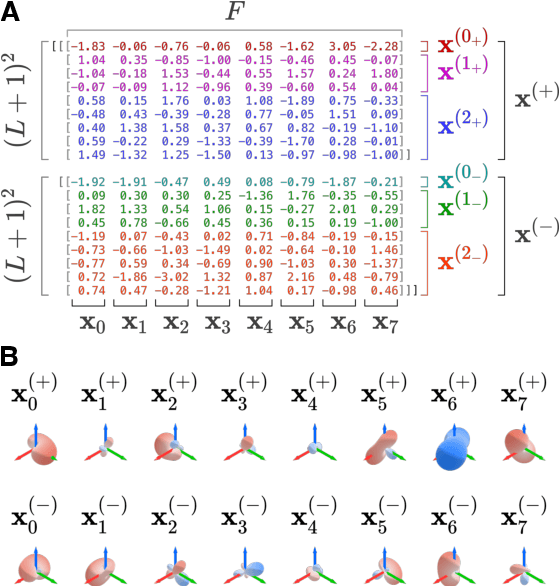
This work introduces E3x, a software package for building neural networks that are equivariant with respect to the Euclidean group $\mathrm{E}(3)$, consisting of translations, rotations, and reflections of three-dimensional space. Compared to ordinary neural networks, $\mathrm{E}(3)$-equivariant models promise benefits whenever input and/or output data are quantities associated with three-dimensional objects. This is because the numeric values of such quantities (e.g. positions) typically depend on the chosen coordinate system. Under transformations of the reference frame, the values change predictably, but the underlying rules can be difficult to learn for ordinary machine learning models. With built-in $\mathrm{E}(3)$-equivariance, neural networks are guaranteed to satisfy the relevant transformation rules exactly, resulting in superior data efficiency and accuracy. The code for E3x is available from https://github.com/google-research/e3x, detailed documentation and usage examples can be found on https://e3x.readthedocs.io.

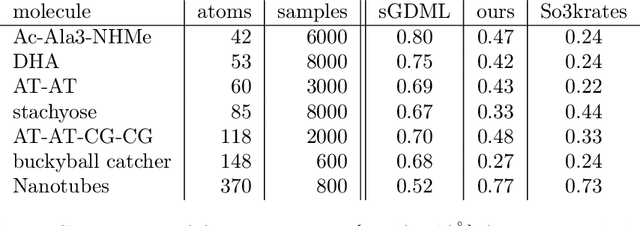
From Peptides to Nanostructures: A Euclidean Transformer for Fast and Stable Machine Learned Force Fields

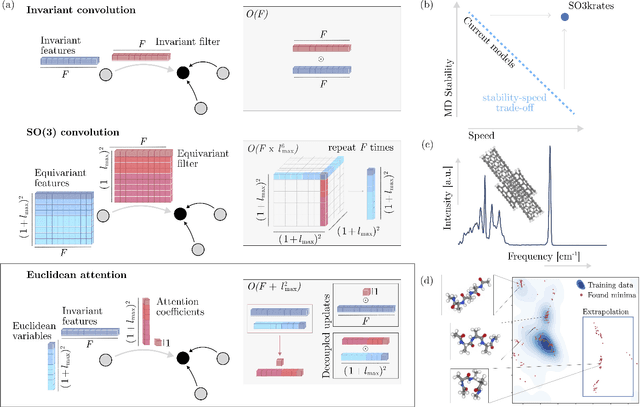
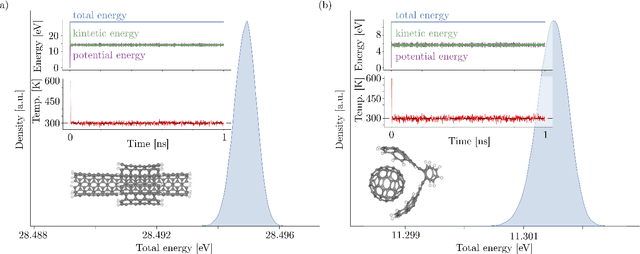
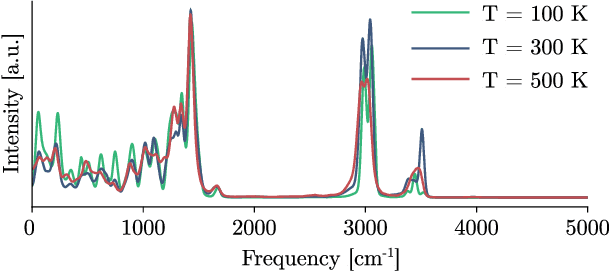
Recent years have seen vast progress in the development of machine learned force fields (MLFFs) based on ab-initio reference calculations. Despite achieving low test errors, the suitability of MLFFs in molecular dynamics (MD) simulations is being increasingly scrutinized due to concerns about instability. Our findings suggest a potential connection between MD simulation stability and the presence of equivariant representations in MLFFs, but their computational cost can limit practical advantages they would otherwise bring. To address this, we propose a transformer architecture called SO3krates that combines sparse equivariant representations (Euclidean variables) with a self-attention mechanism that can separate invariant and equivariant information, eliminating the need for expensive tensor products. SO3krates achieves a unique combination of accuracy, stability, and speed that enables insightful analysis of quantum properties of matter on unprecedented time and system size scales. To showcase this capability, we generate stable MD trajectories for flexible peptides and supra-molecular structures with hundreds of atoms. Furthermore, we investigate the PES topology for medium-sized chainlike molecules (e.g., small peptides) by exploring thousands of minima. Remarkably, SO3krates demonstrates the ability to strike a balance between the conflicting demands of stability and the emergence of new minimum-energy conformations beyond the training data, which is crucial for realistic exploration tasks in the field of biochemistry.