Euclidean Fast Attention: Machine Learning Global Atomic Representations at Linear Cost

Long-range correlations are essential across numerous machine learning tasks, especially for data embedded in Euclidean space, where the relative positions and orientations of distant components are often critical for accurate predictions. Self-attention offers a compelling mechanism for capturing these global effects, but its quadratic complexity presents a significant practical limitation. This problem is particularly pronounced in computational chemistry, where the stringent efficiency requirements of machine learning force fields (MLFFs) often preclude accurately modeling long-range interactions. To address this, we introduce Euclidean fast attention (EFA), a linear-scaling attention-like mechanism designed for Euclidean data, which can be easily incorporated into existing model architectures. A core component of EFA are novel Euclidean rotary positional encodings (ERoPE), which enable efficient encoding of spatial information while respecting essential physical symmetries. We empirically demonstrate that EFA effectively captures diverse long-range effects, enabling EFA-equipped MLFFs to describe challenging chemical interactions for which conventional MLFFs yield incorrect results.

From Peptides to Nanostructures: A Euclidean Transformer for Fast and Stable Machine Learned Force Fields

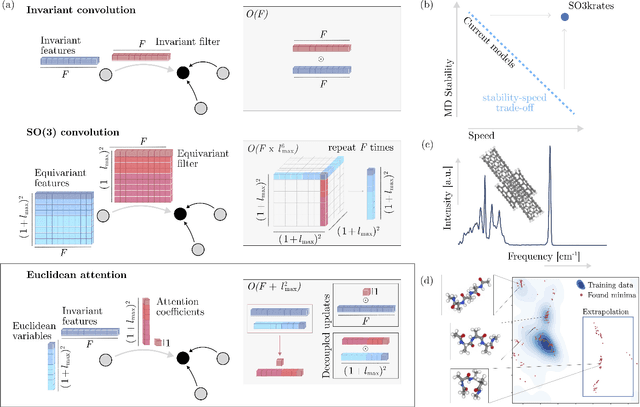
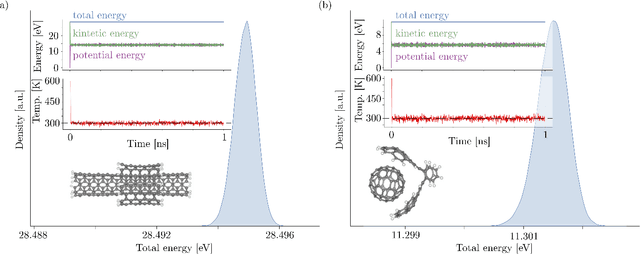
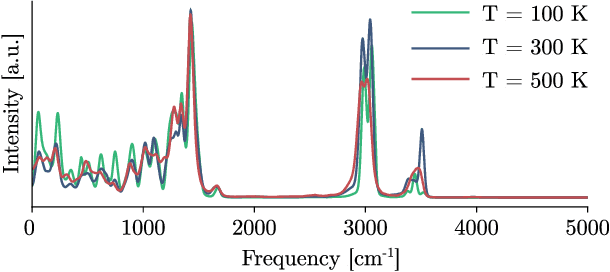
Recent years have seen vast progress in the development of machine learned force fields (MLFFs) based on ab-initio reference calculations. Despite achieving low test errors, the suitability of MLFFs in molecular dynamics (MD) simulations is being increasingly scrutinized due to concerns about instability. Our findings suggest a potential connection between MD simulation stability and the presence of equivariant representations in MLFFs, but their computational cost can limit practical advantages they would otherwise bring. To address this, we propose a transformer architecture called SO3krates that combines sparse equivariant representations (Euclidean variables) with a self-attention mechanism that can separate invariant and equivariant information, eliminating the need for expensive tensor products. SO3krates achieves a unique combination of accuracy, stability, and speed that enables insightful analysis of quantum properties of matter on unprecedented time and system size scales. To showcase this capability, we generate stable MD trajectories for flexible peptides and supra-molecular structures with hundreds of atoms. Furthermore, we investigate the PES topology for medium-sized chainlike molecules (e.g., small peptides) by exploring thousands of minima. Remarkably, SO3krates demonstrates the ability to strike a balance between the conflicting demands of stability and the emergence of new minimum-energy conformations beyond the training data, which is crucial for realistic exploration tasks in the field of biochemistry.

Reconstructing Kernel-based Machine Learning Force Fields with Super-linear Convergence

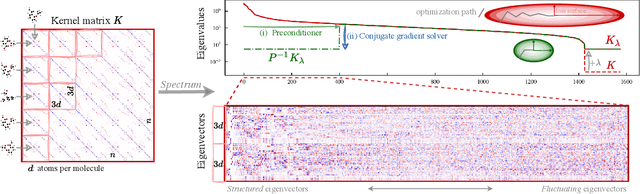
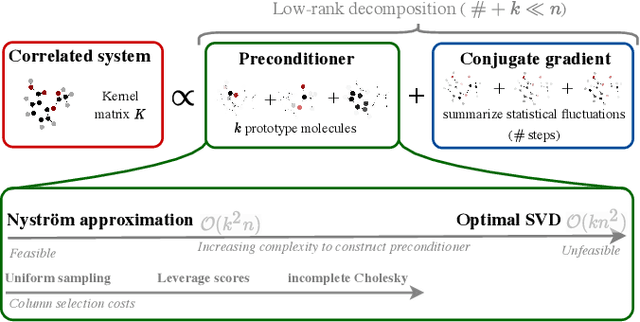
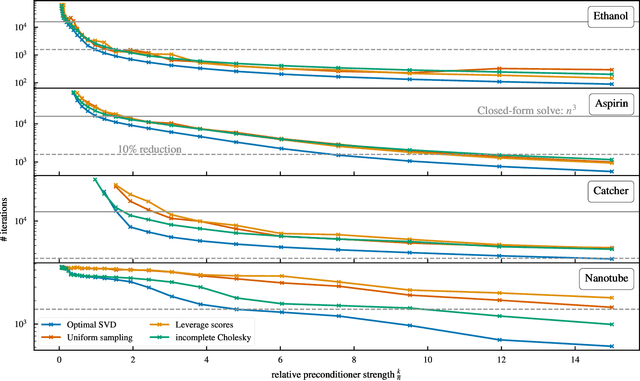
Kernel machines have sustained continuous progress in the field of quantum chemistry. In particular, they have proven to be successful in the low-data regime of force field reconstruction. This is because many physical invariances and symmetries can be incorporated into the kernel function to compensate for much larger datasets. So far, the scalability of this approach has however been hindered by its cubical runtime in the number of training points. While it is known, that iterative Krylov subspace solvers can overcome these burdens, they crucially rely on effective preconditioners, which are elusive in practice. Practical preconditioners need to be computationally efficient and numerically robust at the same time. Here, we consider the broad class of Nystr\"om-type methods to construct preconditioners based on successively more sophisticated low-rank approximations of the original kernel matrix, each of which provides a different set of computational trade-offs. All considered methods estimate the relevant subspace spanned by the kernel matrix columns using different strategies to identify a representative set of inducing points. Our comprehensive study covers the full spectrum of approaches, starting from naive random sampling to leverage score estimates and incomplete Cholesky factorizations, up to exact SVD decompositions.

Algorithmic Differentiation for Automatized Modelling of Machine Learned Force Fields

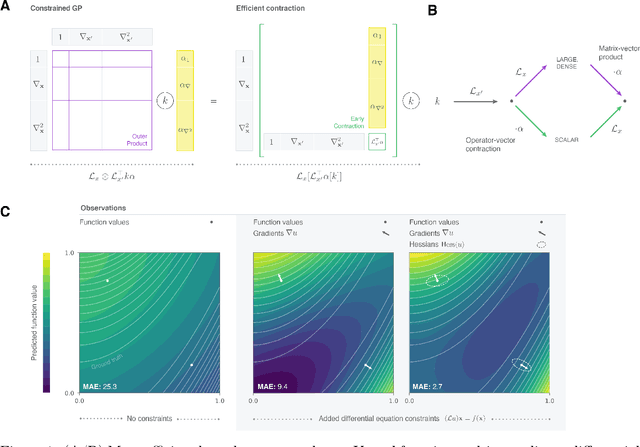
Reconstructing force fields (FF) from atomistic simulation data is a challenge since accurate data can be highly expensive. Here, machine learning (ML) models can help to be data economic as they can be successfully constrained using the underlying symmetry and conservation laws of physics. However, so far, every descriptor newly proposed for an ML model has required a cumbersome and mathematically tedious remodeling. We therefore propose to use modern techniques from algorithmic differentiation within the ML modeling process -- effectively enabling the usage of novel descriptors or models fully automatically at an order of magnitude higher computational efficiency. This paradigmatic approach enables not only a versatile usage of novel representations, the efficient computation of larger systems -- all of high value to the FF community -- but also the simple inclusion of further physical knowledge such as higher-order information (e.g.~Hessians, more complex partial differential equations constraints etc.), even beyond the presented FF domain.

Detect the Interactions that Matter in Matter: Geometric Attention for Many-Body Systems

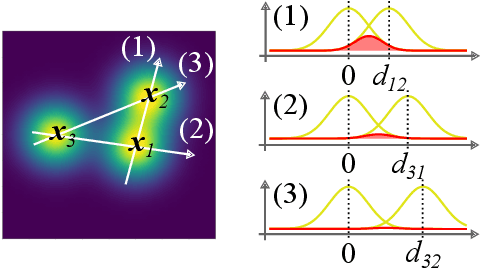
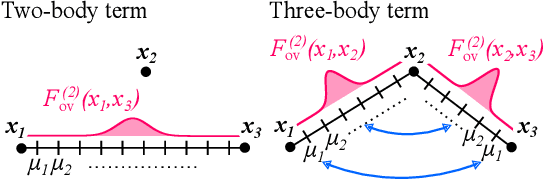
Attention mechanisms are developing into a viable alternative to convolutional layers as elementary building block of NNs. Their main advantage is that they are not restricted to capture local dependencies in the input, but can draw arbitrary connections. This unprecedented capability coincides with the long-standing problem of modeling global atomic interactions in molecular force fields and other many-body problems. In its original formulation, however, attention is not applicable to the continuous domains in which the atoms live. For this purpose we propose a variant to describe geometric relations for arbitrary atomic configurations in Euclidean space that also respects all relevant physical symmetries. We furthermore demonstrate, how the successive application of our learned attention matrices effectively translates the molecular geometry into a set of individual atomic contributions on-the-fly.

BIGDML: Towards Exact Machine Learning Force Fields for Materials

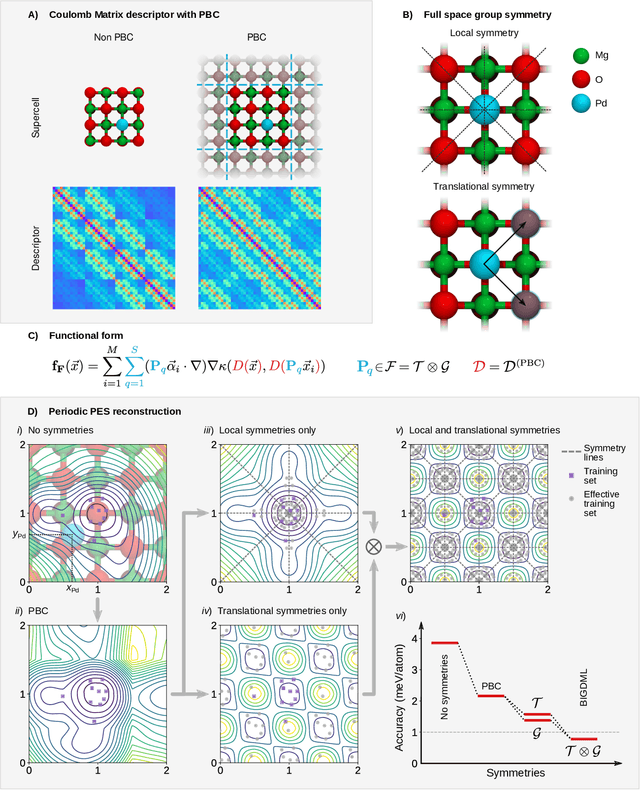
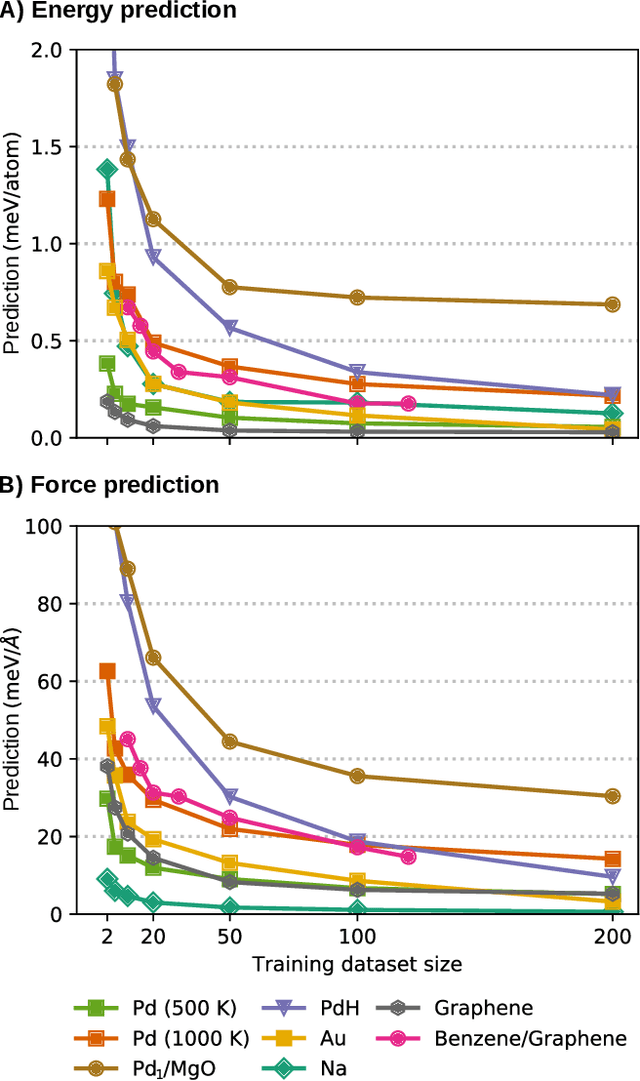
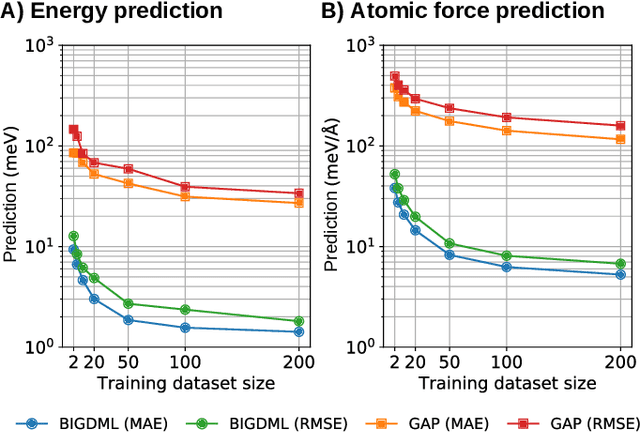
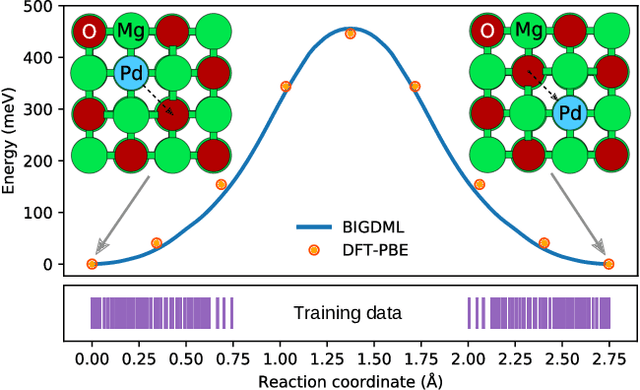
Machine-learning force fields (MLFF) should be accurate, computationally and data efficient, and applicable to molecules, materials, and interfaces thereof. Currently, MLFFs often introduce tradeoffs that restrict their practical applicability to small subsets of chemical space or require exhaustive datasets for training. Here, we introduce the Bravais-Inspired Gradient-Domain Machine Learning (BIGDML) approach and demonstrate its ability to construct reliable force fields using a training set with just 10-200 geometries for materials including pristine and defect-containing 2D and 3D semiconductors and metals, as well as chemisorbed and physisorbed atomic and molecular adsorbates on surfaces. The BIGDML model employs the full relevant symmetry group for a given material, does not assume artificial atom types or localization of atomic interactions and exhibits high data efficiency and state-of-the-art energy accuracies (errors substantially below 1 meV per atom) for an extended set of materials. Extensive path-integral molecular dynamics carried out with BIGDML models demonstrate the counterintuitive localization of benzene--graphene dynamics induced by nuclear quantum effects and allow to rationalize the Arrhenius behavior of hydrogen diffusion coefficient in a Pd crystal for a wide range of temperatures.

SpookyNet: Learning Force Fields with Electronic Degrees of Freedom and Nonlocal Effects

In recent years, machine-learned force fields (ML-FFs) have gained increasing popularity in the field of computational chemistry. Provided they are trained on appropriate reference data, ML-FFs combine the accuracy of ab initio methods with the efficiency of conventional force fields. However, current ML-FFs typically ignore electronic degrees of freedom, such as the total charge or spin, when forming their prediction. In addition, they often assume chemical locality, which can be problematic in cases where nonlocal effects play a significant role. This work introduces SpookyNet, a deep neural network for constructing ML-FFs with explicit treatment of electronic degrees of freedom and quantum nonlocality. Its predictions are further augmented with physically-motivated corrections to improve the description of long-ranged interactions and nuclear repulsion. SpookyNet improves upon the current state-of-the-art (or achieves similar performance) on popular quantum chemistry data sets. Notably, it can leverage the learned chemical insights, e.g. by predicting unknown spin states or by properly modeling physical limits. Moreover, it is able to generalize across chemical and conformational space and thus close an important remaining gap for today's machine learning models in quantum chemistry.

Machine Learning Force Fields

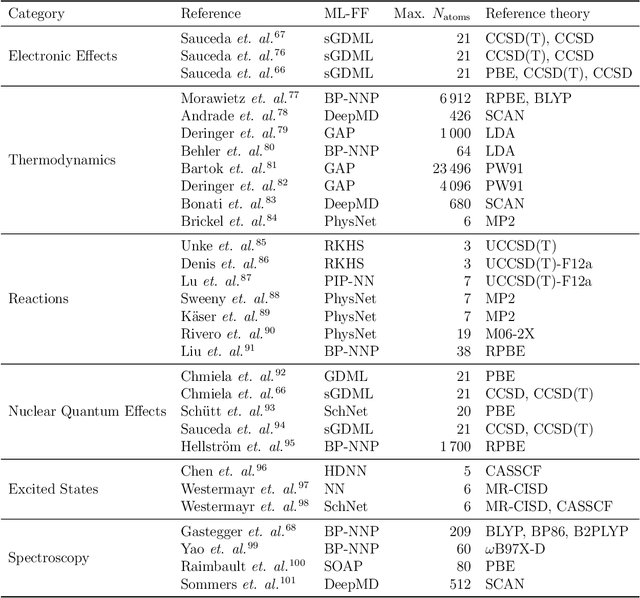
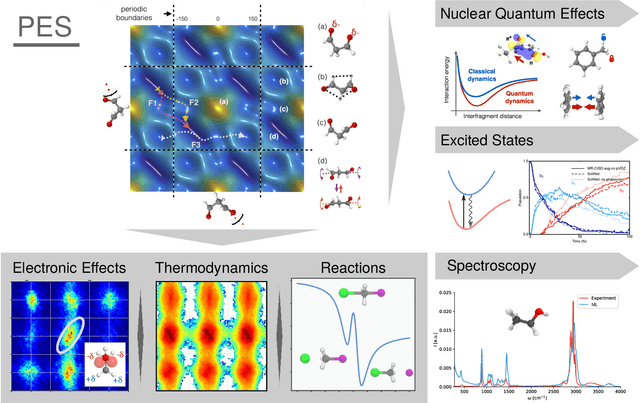
In recent years, the use of Machine Learning (ML) in computational chemistry has enabled numerous advances previously out of reach due to the computational complexity of traditional electronic-structure methods. One of the most promising applications is the construction of ML-based force fields (FFs), with the aim to narrow the gap between the accuracy of ab initio methods and the efficiency of classical FFs. The key idea is to learn the statistical relation between chemical structure and potential energy without relying on a preconceived notion of fixed chemical bonds or knowledge about the relevant interactions. Such universal ML approximations are in principle only limited by the quality and quantity of the reference data used to train them. This review gives an overview of applications of ML-FFs and the chemical insights that can be obtained from them. The core concepts underlying ML-FFs are described in detail and a step-by-step guide for constructing and testing them from scratch is given. The text concludes with a discussion of the challenges that remain to be overcome by the next generation of ML-FFs.

Ensemble Learning of Coarse-Grained Molecular Dynamics Force Fields with a Kernel Approach

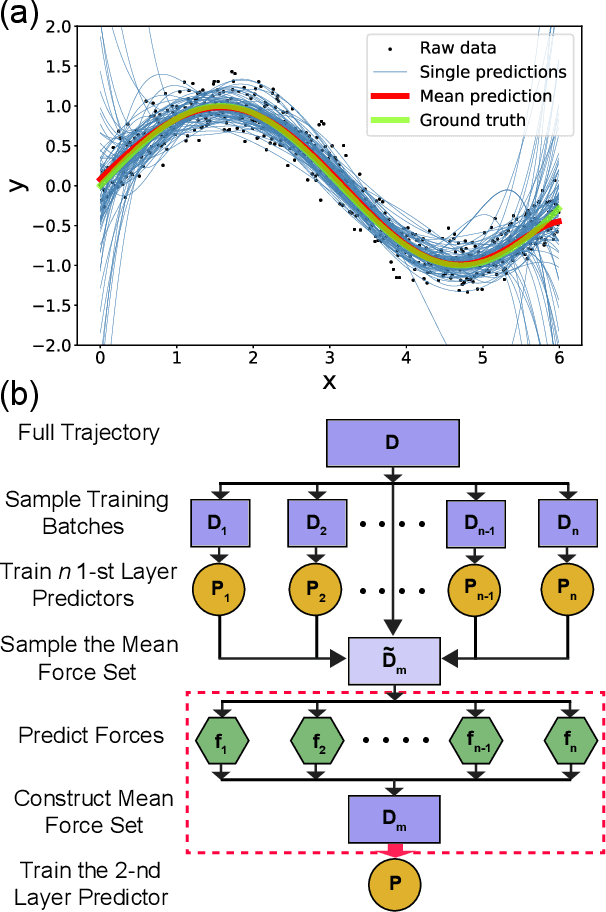
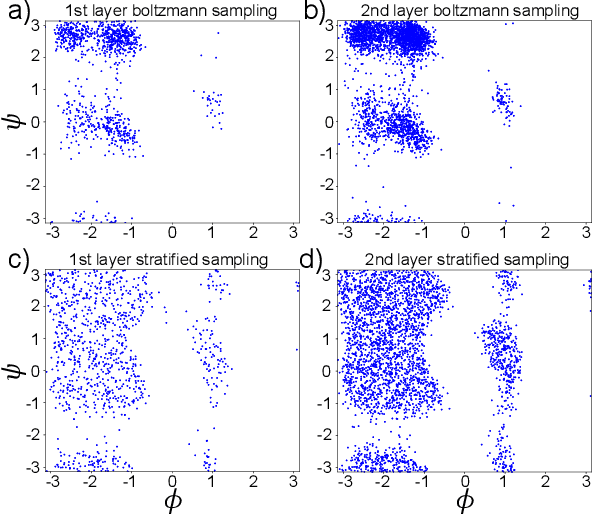
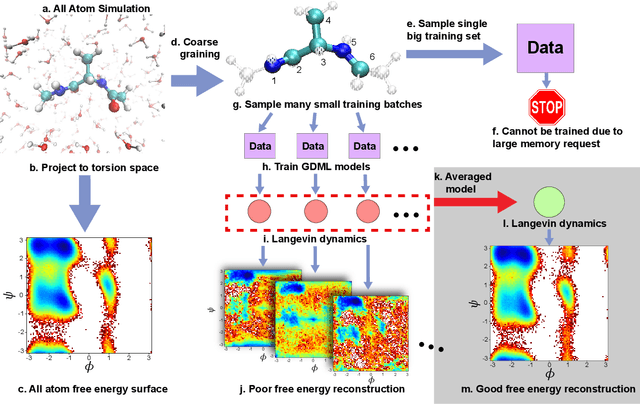
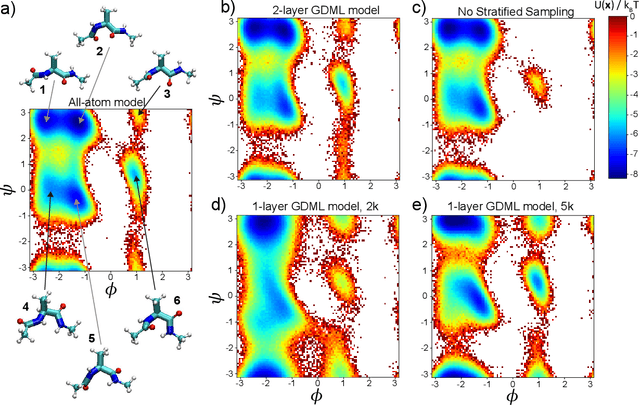
Gradient-domain machine learning (GDML) is an accurate and efficient approach to learn a molecular potential and associated force field based on the kernel ridge regression algorithm. Here, we demonstrate its application to learn an effective coarse-grained (CG) model from all-atom simulation data in a sample efficient manner. The coarse-grained force field is learned by following the thermodynamic consistency principle, here by minimizing the error between the predicted coarse-grained force and the all-atom mean force in the coarse-grained coordinates. Solving this problem by GDML directly is impossible because coarse-graining requires averaging over many training data points, resulting in impractical memory requirements for storing the kernel matrices. In this work, we propose a data-efficient and memory-saving alternative. Using ensemble learning and stratified sampling, we propose a 2-layer training scheme that enables GDML to learn an effective coarse-grained model. We illustrate our method on a simple biomolecular system, alanine dipeptide, by reconstructing the free energy landscape of a coarse-grained variant of this molecule. Our novel GDML training scheme yields a smaller free energy error than neural networks when the training set is small, and a comparably high accuracy when the training set is sufficiently large.

SchNet: A continuous-filter convolutional neural network for modeling quantum interactions

Deep learning has the potential to revolutionize quantum chemistry as it is ideally suited to learn representations for structured data and speed up the exploration of chemical space. While convolutional neural networks have proven to be the first choice for images, audio and video data, the atoms in molecules are not restricted to a grid. Instead, their precise locations contain essential physical information, that would get lost if discretized. Thus, we propose to use continuous-filter convolutional layers to be able to model local correlations without requiring the data to lie on a grid. We apply those layers in SchNet: a novel deep learning architecture modeling quantum interactions in molecules. We obtain a joint model for the total energy and interatomic forces that follows fundamental quantum-chemical principles. This includes rotationally invariant energy predictions and a smooth, differentiable potential energy surface. Our architecture achieves state-of-the-art performance for benchmarks of equilibrium molecules and molecular dynamics trajectories. Finally, we introduce a more challenging benchmark with chemical and structural variations that suggests the path for further work.