Learning Hamiltonian Flow Maps: Mean Flow Consistency for Large-Timestep Molecular Dynamics

Simulating the long-time evolution of Hamiltonian systems is limited by the small timesteps required for stable numerical integration. To overcome this constraint, we introduce a framework to learn Hamiltonian Flow Maps by predicting the mean phase-space evolution over a chosen time span $Δt$, enabling stable large-timestep updates far beyond the stability limits of classical integrators. To this end, we impose a Mean Flow consistency condition for time-averaged Hamiltonian dynamics. Unlike prior approaches, this allows training on independent phase-space samples without access to future states, avoiding expensive trajectory generation. Validated across diverse Hamiltonian systems, our method in particular improves upon molecular dynamics simulations using machine-learned force fields (MLFF). Our models maintain comparable training and inference cost, but support significantly larger integration timesteps while trained directly on widely-available trajectory-free MLFF datasets.

Detect the Interactions that Matter in Matter: Geometric Attention for Many-Body Systems

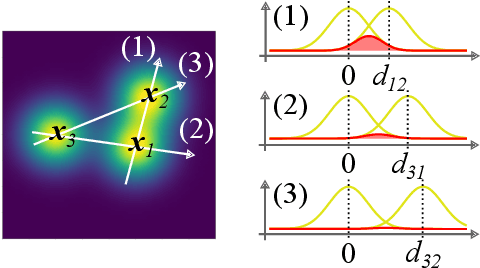
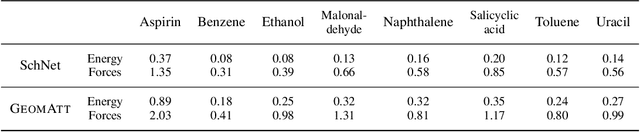
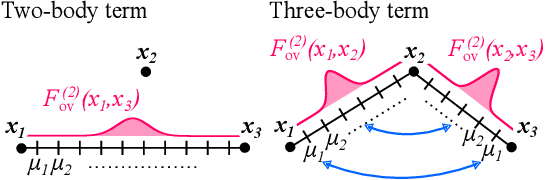
Attention mechanisms are developing into a viable alternative to convolutional layers as elementary building block of NNs. Their main advantage is that they are not restricted to capture local dependencies in the input, but can draw arbitrary connections. This unprecedented capability coincides with the long-standing problem of modeling global atomic interactions in molecular force fields and other many-body problems. In its original formulation, however, attention is not applicable to the continuous domains in which the atoms live. For this purpose we propose a variant to describe geometric relations for arbitrary atomic configurations in Euclidean space that also respects all relevant physical symmetries. We furthermore demonstrate, how the successive application of our learned attention matrices effectively translates the molecular geometry into a set of individual atomic contributions on-the-fly.