Doob's Lagrangian: A Sample-Efficient Variational Approach to Transition Path Sampling

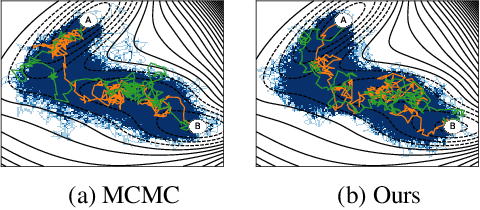
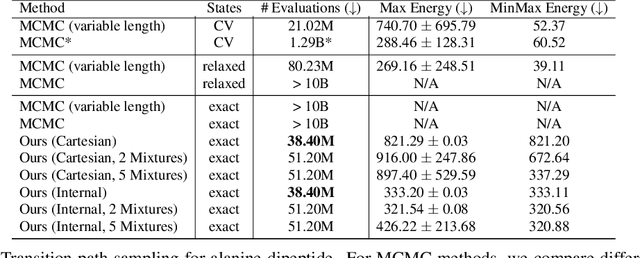
Rare event sampling in dynamical systems is a fundamental problem arising in the natural sciences, which poses significant computational challenges due to an exponentially large space of trajectories. For settings where the dynamical system of interest follows a Brownian motion with known drift, the question of conditioning the process to reach a given endpoint or desired rare event is definitively answered by Doob's h-transform. However, the naive estimation of this transform is infeasible, as it requires simulating sufficiently many forward trajectories to estimate rare event probabilities. In this work, we propose a variational formulation of Doob's $h$-transform as an optimization problem over trajectories between a given initial point and the desired ending point. To solve this optimization, we propose a simulation-free training objective with a model parameterization that imposes the desired boundary conditions by design. Our approach significantly reduces the search space over trajectories and avoids expensive trajectory simulation and inefficient importance sampling estimators which are required in existing methods. We demonstrate the ability of our method to find feasible transition paths on real-world molecular simulation and protein folding tasks.

Highly Accurate Real-space Electron Densities with Neural Networks

Variational ab-initio methods in quantum chemistry stand out among other methods in providing direct access to the wave function. This allows in principle straightforward extraction of any other observable of interest, besides the energy, but in practice this extraction is often technically difficult and computationally impractical. Here, we consider the electron density as a central observable in quantum chemistry and introduce a novel method to obtain accurate densities from real-space many-electron wave functions by representing the density with a neural network that captures known asymptotic properties and is trained from the wave function by score matching and noise-contrastive estimation. We use variational quantum Monte Carlo with deep-learning ans\"atze (deep QMC) to obtain highly accurate wave functions free of basis set errors, and from them, using our novel method, correspondingly accurate electron densities, which we demonstrate by calculating dipole moments, nuclear forces, contact densities, and other density-based properties.

Artificially intelligent Maxwell's demon for optimal control of open quantum systems

Feedback control of open quantum systems is of fundamental importance for practical applications in various contexts, ranging from quantum computation to quantum error correction and quantum metrology. Its use in the context of thermodynamics further enables the study of the interplay between information and energy. However, deriving optimal feedback control strategies is highly challenging, as it involves the optimal control of open quantum systems, the stochastic nature of quantum measurement, and the inclusion of policies that maximize a long-term time- and trajectory-averaged goal. In this work, we employ a reinforcement learning approach to automate and capture the role of a quantum Maxwell's demon: the agent takes the literal role of discovering optimal feedback control strategies in qubit-based systems that maximize a trade-off between measurement-powered cooling and measurement efficiency. Considering weak or projective quantum measurements, we explore different regimes based on the ordering between the thermalization, the measurement, and the unitary feedback timescales, finding different and highly non-intuitive, yet interpretable, strategies. In the thermalization-dominated regime, we find strategies with elaborate finite-time thermalization protocols conditioned on measurement outcomes. In the measurement-dominated regime, we find that optimal strategies involve adaptively measuring different qubit observables reflecting the acquired information, and repeating multiple weak measurements until the quantum state is "sufficiently pure", leading to random walks in state space. Finally, we study the case when all timescales are comparable, finding new feedback control strategies that considerably outperform more intuitive ones. We discuss a two-qubit example where we explore the role of entanglement and conclude discussing the scaling of our results to quantum many-body systems.

Transferable Boltzmann Generators

The generation of equilibrium samples of molecular systems has been a long-standing problem in statistical physics. Boltzmann Generators are a generative machine learning method that addresses this issue by learning a transformation via a normalizing flow from a simple prior distribution to the target Boltzmann distribution of interest. Recently, flow matching has been employed to train Boltzmann Generators for small molecular systems in Cartesian coordinates. We extend this work and propose a first framework for Boltzmann Generators that are transferable across chemical space, such that they predict zero-shot Boltzmann distributions for test molecules without being retrained for these systems. These transferable Boltzmann Generators allow approximate sampling from the target distribution of unseen systems, as well as efficient reweighting to the target Boltzmann distribution. The transferability of the proposed framework is evaluated on dipeptides, where we show that it generalizes efficiently to unseen systems. Furthermore, we demonstrate that our proposed architecture enhances the efficiency of Boltzmann Generators trained on single molecular systems.

Efficient mapping of phase diagrams with conditional normalizing flows

The accurate prediction of phase diagrams is of central importance for both the fundamental understanding of materials as well as for technological applications in material sciences. However, the computational prediction of the relative stability between phases based on their free energy is a daunting task, as traditional free energy estimators require a large amount of simulation data to obtain uncorrelated equilibrium samples over a grid of thermodynamic states. In this work, we develop deep generative machine learning models for entire phase diagrams, employing normalizing flows conditioned on the thermodynamic states, e.g., temperature and pressure, that they map to. By training a single normalizing flow to transform the equilibrium distribution sampled at only one reference thermodynamic state to a wide range of target temperatures and pressures, we can efficiently generate equilibrium samples across the entire phase diagram. Using a permutation-equivariant architecture allows us, thereby, to treat solid and liquid phases on the same footing. We demonstrate our approach by predicting the solid-liquid coexistence line for a Lennard-Jones system in excellent agreement with state-of-the-art free energy methods while significantly reducing the number of energy evaluations needed.

PILOT: Equivariant diffusion for pocket conditioned de novo ligand generation with multi-objective guidance via importance sampling

The generation of ligands that both are tailored to a given protein pocket and exhibit a range of desired chemical properties is a major challenge in structure-based drug design. Here, we propose an in-silico approach for the $\textit{de novo}$ generation of 3D ligand structures using the equivariant diffusion model PILOT, combining pocket conditioning with a large-scale pre-training and property guidance. Its multi-objective trajectory-based importance sampling strategy is designed to direct the model towards molecules that not only exhibit desired characteristics such as increased binding affinity for a given protein pocket but also maintains high synthetic accessibility. This ensures the practicality of sampled molecules, thus maximizing their potential for the drug discovery pipeline. PILOT significantly outperforms existing methods across various metrics on the common benchmark dataset CrossDocked2020. Moreover, we employ PILOT to generate novel ligands for unseen protein pockets from the Kinodata-3D dataset, which encompasses a substantial portion of the human kinome. The generated structures exhibit predicted $IC_{50}$ values indicative of potent biological activity, which highlights the potential of PILOT as a powerful tool for structure-based drug design.

Improved motif-scaffolding with SE(3) flow matching

Protein design often begins with knowledge of a desired function from a motif which motif-scaffolding aims to construct a functional protein around. Recently, generative models have achieved breakthrough success in designing scaffolds for a diverse range of motifs. However, the generated scaffolds tend to lack structural diversity, which can hinder success in wet-lab validation. In this work, we extend FrameFlow, an SE(3) flow matching model for protein backbone generation, to perform motif-scaffolding with two complementary approaches. The first is motif amortization, in which FrameFlow is trained with the motif as input using a data augmentation strategy. The second is motif guidance, which performs scaffolding using an estimate of the conditional score from FrameFlow, and requires no additional training. Both approaches achieve an equivalent or higher success rate than previous state-of-the-art methods, with 2.5 times more structurally diverse scaffolds. Code: https://github.com/ microsoft/frame-flow.

Navigating protein landscapes with a machine-learned transferable coarse-grained model

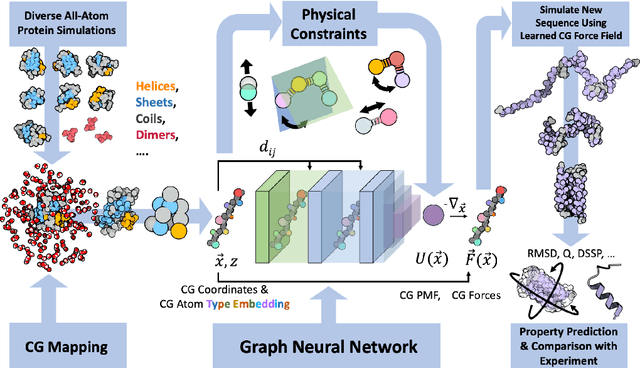
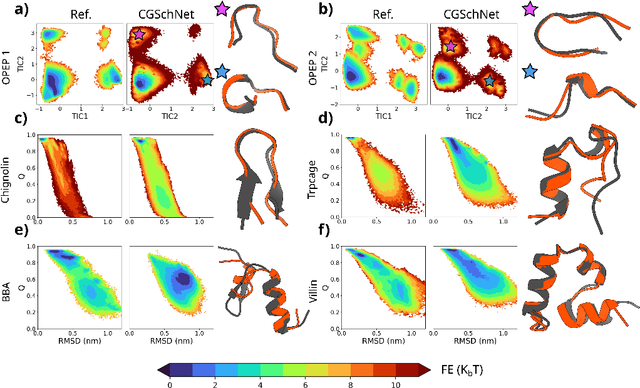
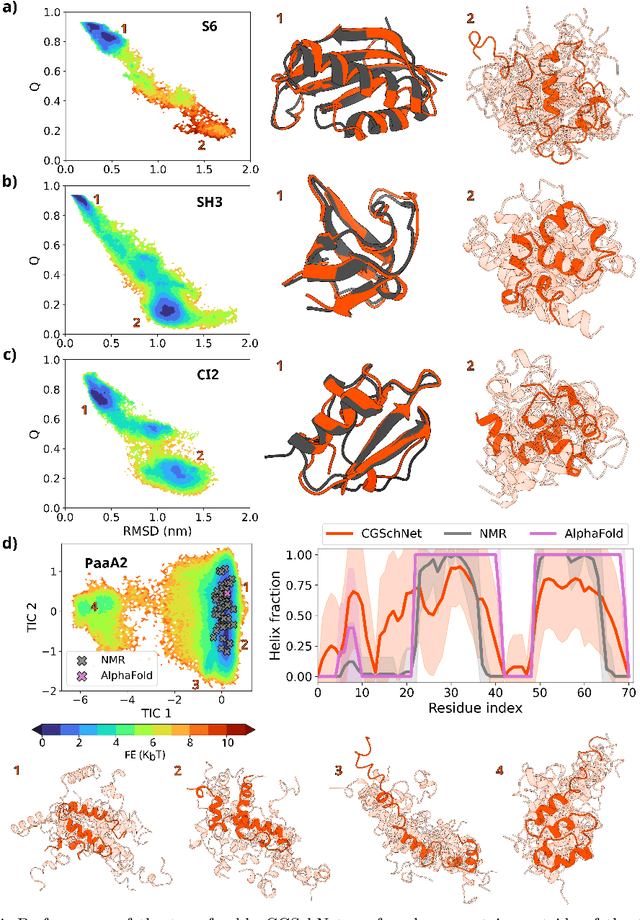
The most popular and universally predictive protein simulation models employ all-atom molecular dynamics (MD), but they come at extreme computational cost. The development of a universal, computationally efficient coarse-grained (CG) model with similar prediction performance has been a long-standing challenge. By combining recent deep learning methods with a large and diverse training set of all-atom protein simulations, we here develop a bottom-up CG force field with chemical transferability, which can be used for extrapolative molecular dynamics on new sequences not used during model parametrization. We demonstrate that the model successfully predicts folded structures, intermediates, metastable folded and unfolded basins, and the fluctuations of intrinsically disordered proteins while it is several orders of magnitude faster than an all-atom model. This showcases the feasibility of a universal and computationally efficient machine-learned CG model for proteins.

Navigating the Design Space of Equivariant Diffusion-Based Generative Models for De Novo 3D Molecule Generation

Deep generative diffusion models are a promising avenue for de novo 3D molecular design in material science and drug discovery. However, their utility is still constrained by suboptimal performance with large molecular structures and limited training data. Addressing this gap, we explore the design space of E(3) equivariant diffusion models, focusing on previously blank spots. Our extensive comparative analysis evaluates the interplay between continuous and discrete state spaces. Out of this investigation, we introduce the EQGAT-diff model, which consistently surpasses the performance of established models on the QM9 and GEOM-Drugs datasets by a large margin. Distinctively, EQGAT-diff takes continuous atomic positions while chemical elements and bond types are categorical and employ a time-dependent loss weighting that significantly increases training convergence and the quality of generated samples. To further strengthen the applicability of diffusion models to limited training data, we examine the transferability of EQGAT-diff trained on the large PubChem3D dataset with implicit hydrogens to target distributions with explicit hydrogens. Fine-tuning EQGAT-diff for a couple of iterations further pushes state-of-the-art performance across datasets. We envision that our findings will find applications in structure-based drug design, where the accuracy of generative models for small datasets of complex molecules is critical.

Reaction coordinate flows for model reduction of molecular kinetics

In this work, we introduce a flow based machine learning approach, called reaction coordinate (RC) flow, for discovery of low-dimensional kinetic models of molecular systems. The RC flow utilizes a normalizing flow to design the coordinate transformation and a Brownian dynamics model to approximate the kinetics of RC, where all model parameters can be estimated in a data-driven manner. In contrast to existing model reduction methods for molecular kinetics, RC flow offers a trainable and tractable model of reduced kinetics in continuous time and space due to the invertibility of the normalizing flow. Furthermore, the Brownian dynamics-based reduced kinetic model investigated in this work yields a readily discernible representation of metastable states within the phase space of the molecular system. Numerical experiments demonstrate how effectively the proposed method discovers interpretable and accurate low-dimensional representations of given full-state kinetics from simulations.