Navigating protein landscapes with a machine-learned transferable coarse-grained model

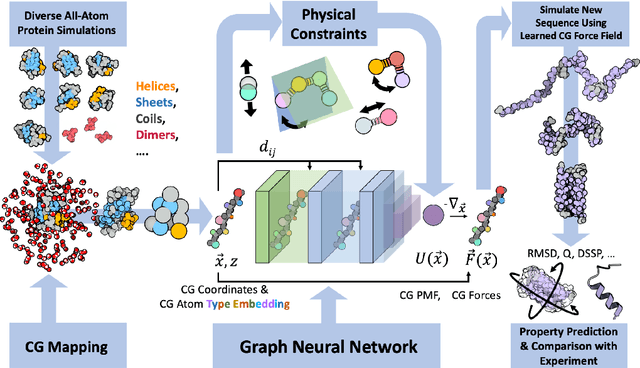
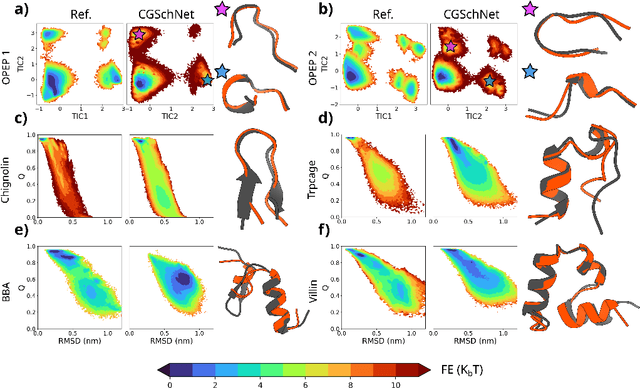
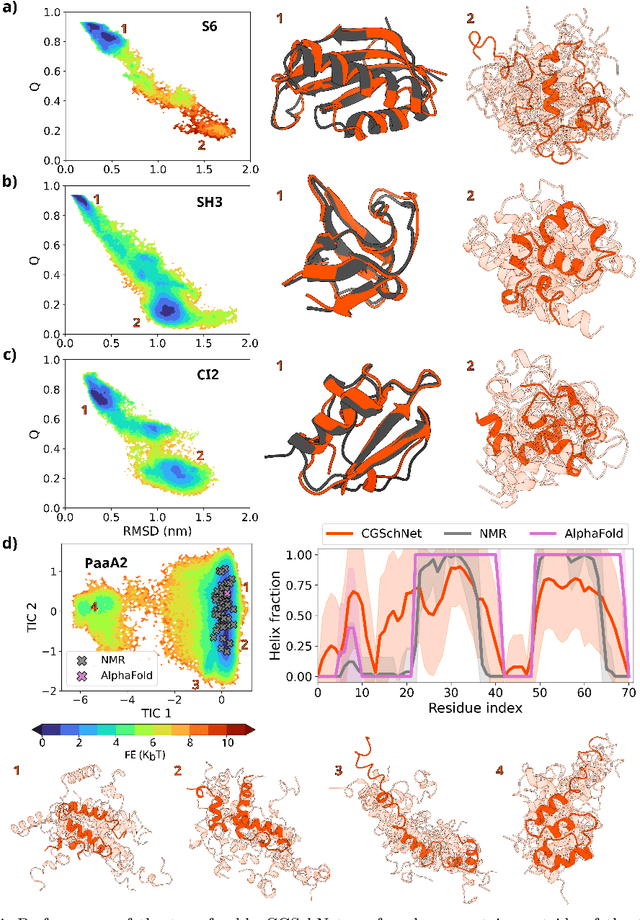
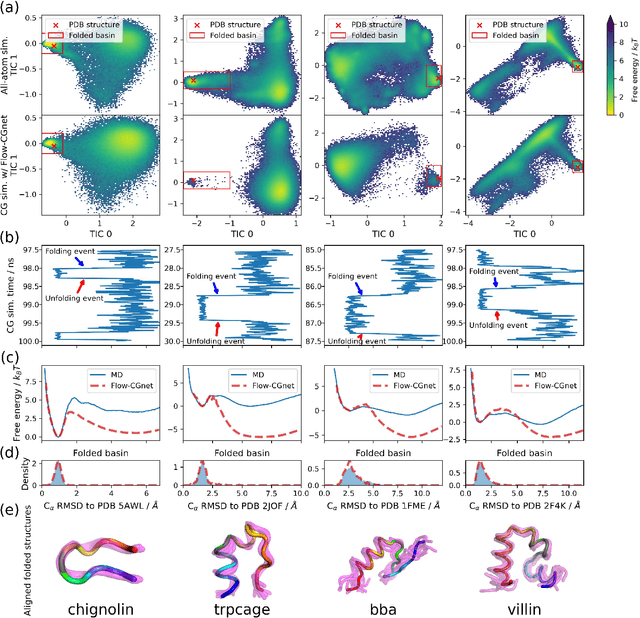
The most popular and universally predictive protein simulation models employ all-atom molecular dynamics (MD), but they come at extreme computational cost. The development of a universal, computationally efficient coarse-grained (CG) model with similar prediction performance has been a long-standing challenge. By combining recent deep learning methods with a large and diverse training set of all-atom protein simulations, we here develop a bottom-up CG force field with chemical transferability, which can be used for extrapolative molecular dynamics on new sequences not used during model parametrization. We demonstrate that the model successfully predicts folded structures, intermediates, metastable folded and unfolded basins, and the fluctuations of intrinsically disordered proteins while it is several orders of magnitude faster than an all-atom model. This showcases the feasibility of a universal and computationally efficient machine-learned CG model for proteins.

OpenMM 8: Molecular Dynamics Simulation with Machine Learning Potentials

Machine learning plays an important and growing role in molecular simulation. The newest version of the OpenMM molecular dynamics toolkit introduces new features to support the use of machine learning potentials. Arbitrary PyTorch models can be added to a simulation and used to compute forces and energy. A higher-level interface allows users to easily model their molecules of interest with general purpose, pretrained potential functions. A collection of optimized CUDA kernels and custom PyTorch operations greatly improves the speed of simulations. We demonstrate these features on simulations of cyclin-dependent kinase 8 (CDK8) and the green fluorescent protein (GFP) chromophore in water. Taken together, these features make it practical to use machine learning to improve the accuracy of simulations at only a modest increase in cost.

Equivariant flow matching

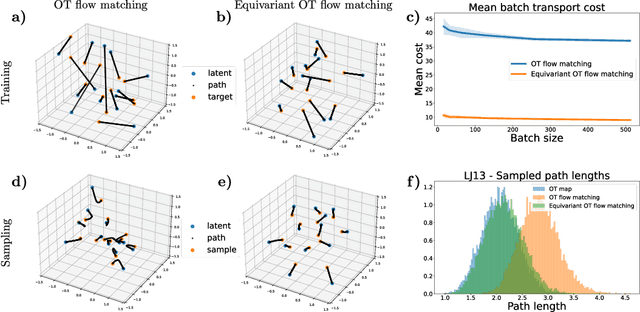
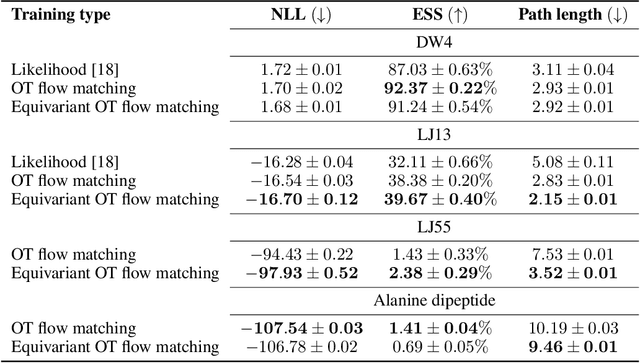
Normalizing flows are a class of deep generative models that are especially interesting for modeling probability distributions in physics, where the exact likelihood of flows allows reweighting to known target energy functions and computing unbiased observables. For instance, Boltzmann generators tackle the long-standing sampling problem in statistical physics by training flows to produce equilibrium samples of many-body systems such as small molecules and proteins. To build effective models for such systems, it is crucial to incorporate the symmetries of the target energy into the model, which can be achieved by equivariant continuous normalizing flows (CNFs). However, CNFs can be computationally expensive to train and generate samples from, which has hampered their scalability and practical application. In this paper, we introduce equivariant flow matching, a new training objective for equivariant CNFs that is based on the recently proposed optimal transport flow matching. Equivariant flow matching exploits the physical symmetries of the target energy for efficient, simulation-free training of equivariant CNFs. We demonstrate the effectiveness of our approach on many-particle systems and a small molecule, alanine dipeptide, where for the first time we obtain a Boltzmann generator with significant sampling efficiency without relying on tailored internal coordinate featurization. Our results show that the equivariant flow matching objective yields flows with shorter integration paths, improved sampling efficiency, and higher scalability compared to existing methods.

Statistically Optimal Force Aggregation for Coarse-Graining Molecular Dynamics

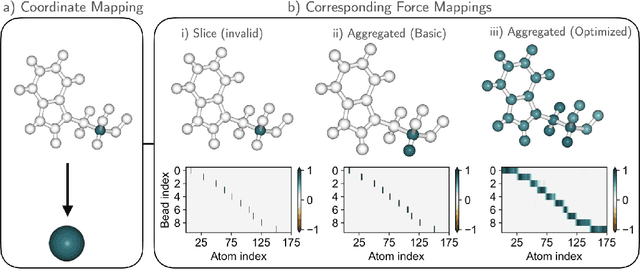
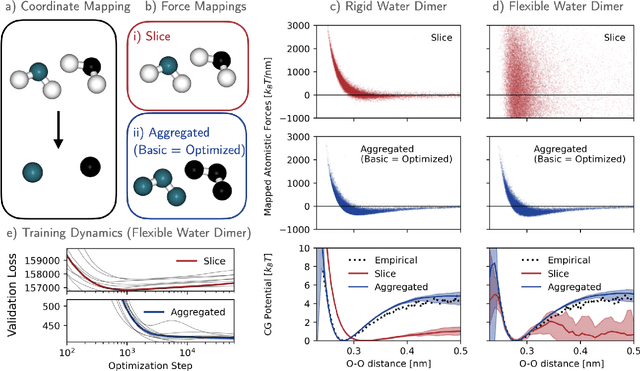
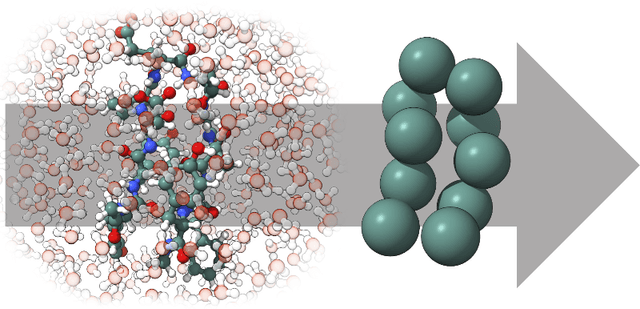
Machine-learned coarse-grained (CG) models have the potential for simulating large molecular complexes beyond what is possible with atomistic molecular dynamics. However, training accurate CG models remains a challenge. A widely used methodology for learning CG force-fields maps forces from all-atom molecular dynamics to the CG representation and matches them with a CG force-field on average. We show that there is flexibility in how to map all-atom forces to the CG representation, and that the most commonly used mapping methods are statistically inefficient and potentially even incorrect in the presence of constraints in the all-atom simulation. We define an optimization statement for force mappings and demonstrate that substantially improved CG force-fields can be learned from the same simulation data when using optimized force maps. The method is demonstrated on the miniproteins Chignolin and Tryptophan Cage and published as open-source code.

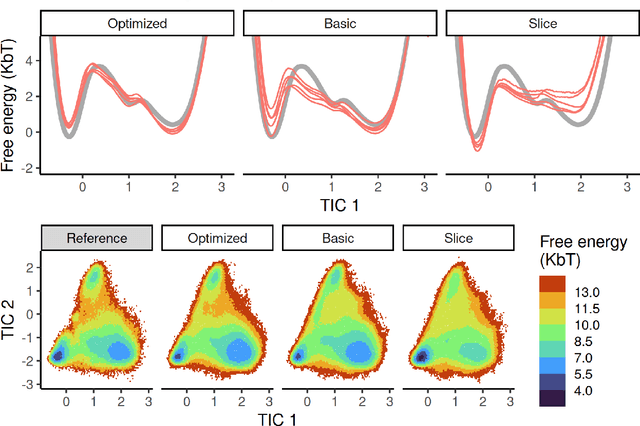
Force-matching Coarse-Graining without Forces

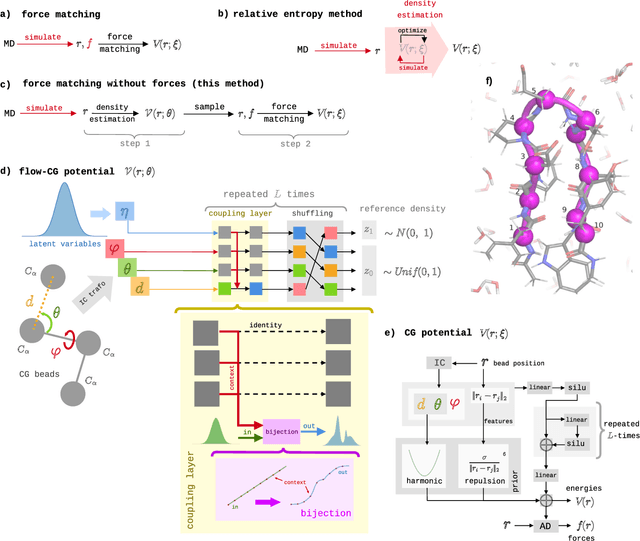
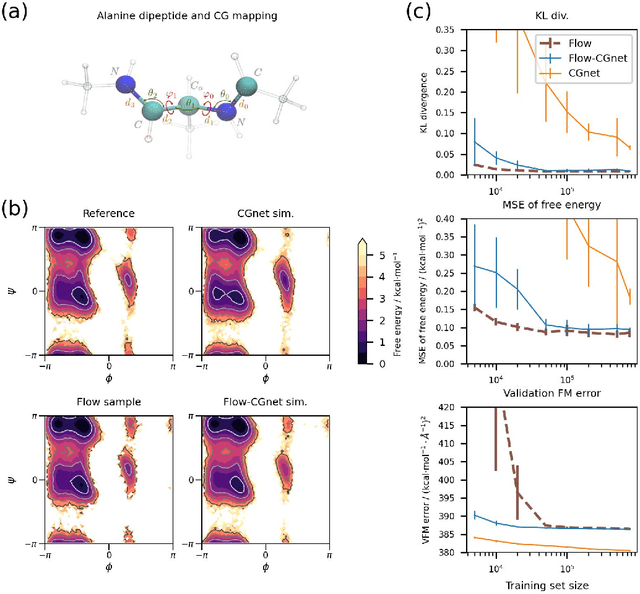
Coarse-grained (CG) molecular simulations have become a standard tool to study molecular processes on time-~and length-scales inaccessible to all-atom simulations. Learning CG force fields from all-atom data has mainly relied on force-matching and relative entropy minimization. Force-matching is straightforward to implement but requires the forces on the CG particles to be saved during all-atom simulation, and because these instantaneous forces depend on all degrees of freedom, they provide a very noisy signal that makes training the CG force field data inefficient. Relative entropy minimization does not require forces to be saved and is more data-efficient, but requires the CG model to be re-simulated during the iterative training procedure, which can make the training procedure extremely costly or lead to failure to converge. Here we present \emph{flow-matching}, a new training method for CG force fields that combines the advantages of force-matching and relative entropy minimization by leveraging normalizing flows, a generative deep learning method. Flow-matching first trains a normalizing flow to represent the CG probability density by using relative entropy minimization without suffering from the re-simulation problem because flows can directly sample from the equilibrium distribution they represent. Subsequently, the forces of the flow are used to train a CG force field by matching the coarse-grained forces directly, which is a much easier problem than traditional force-matching as it does not suffer from the noise problem. Besides not requiring forces, flow-matching also outperforms classical force-matching by an order of magnitude in terms of data efficiency and produces CG models that can capture the folding and unfolding of small proteins.

Smooth Normalizing Flows

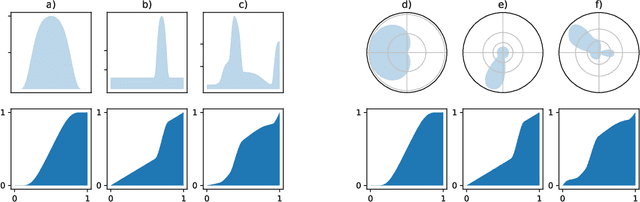
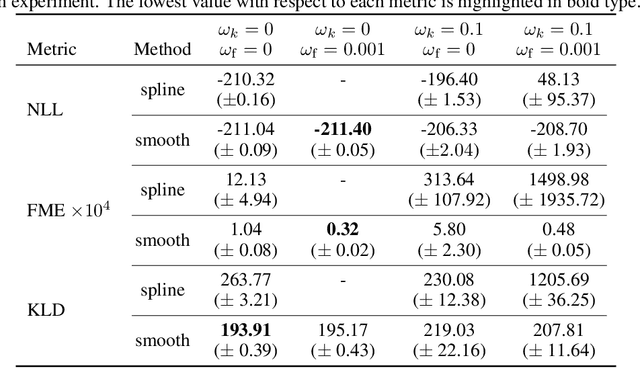
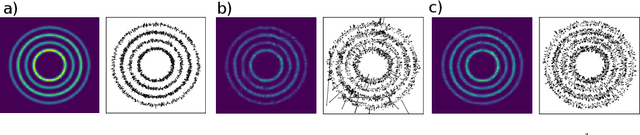
Normalizing flows are a promising tool for modeling probability distributions in physical systems. While state-of-the-art flows accurately approximate distributions and energies, applications in physics additionally require smooth energies to compute forces and higher-order derivatives. Furthermore, such densities are often defined on non-trivial topologies. A recent example are Boltzmann Generators for generating 3D-structures of peptides and small proteins. These generative models leverage the space of internal coordinates (dihedrals, angles, and bonds), which is a product of hypertori and compact intervals. In this work, we introduce a class of smooth mixture transformations working on both compact intervals and hypertori. Mixture transformations employ root-finding methods to invert them in practice, which has so far prevented bi-directional flow training. To this end, we show that parameter gradients and forces of such inverses can be computed from forward evaluations via the inverse function theorem. We demonstrate two advantages of such smooth flows: they allow training by force matching to simulation data and can be used as potentials in molecular dynamics simulations.

Lettuce: PyTorch-based Lattice Boltzmann Framework

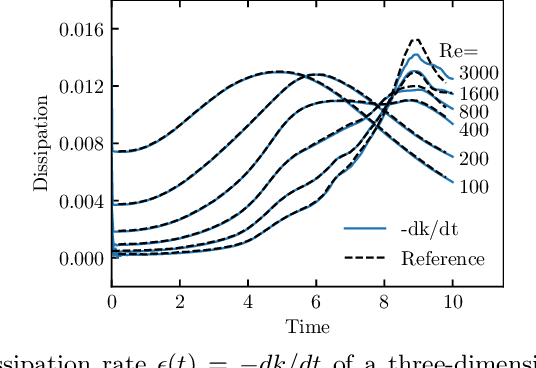
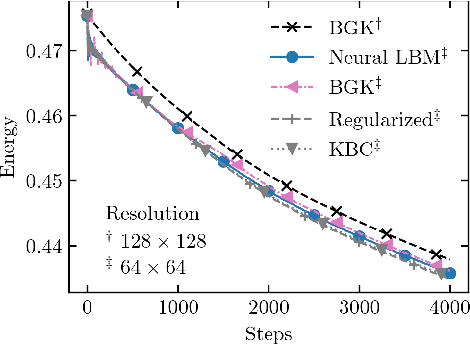
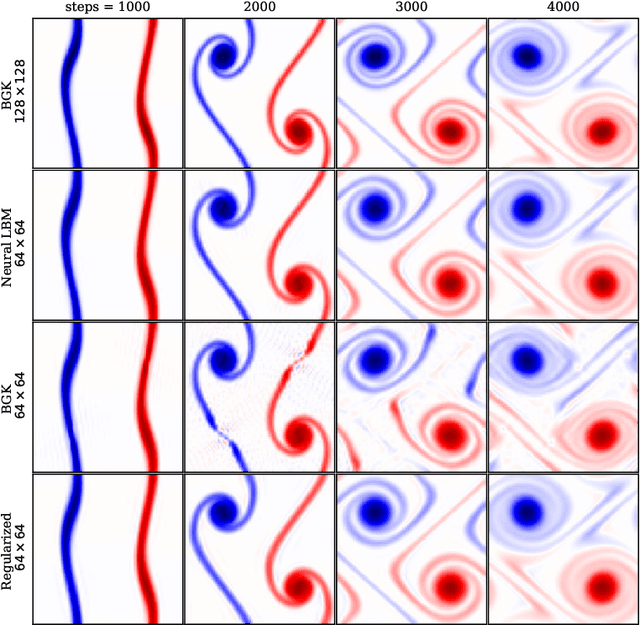
The lattice Boltzmann method (LBM) is an efficient simulation technique for computational fluid mechanics and beyond. It is based on a simple stream-and-collide algorithm on Cartesian grids, which is easily compatible with modern machine learning architectures. While it is becoming increasingly clear that deep learning can provide a decisive stimulus for classical simulation techniques, recent studies have not addressed possible connections between machine learning and LBM. Here, we introduce Lettuce, a PyTorch-based LBM code with a threefold aim. Lettuce enables GPU accelerated calculations with minimal source code, facilitates rapid prototyping of LBM models, and enables integrating LBM simulations with PyTorch's deep learning and automatic differentiation facility. As a proof of concept for combining machine learning with the LBM, a neural collision model is developed, trained on a doubly periodic shear layer and then transferred to a different flow, a decaying turbulence. We also exemplify the added benefit of PyTorch's automatic differentiation framework in flow control and optimization. To this end, the spectrum of a forced isotropic turbulence is maintained without further constraining the velocity field. The source code is freely available from https://github.com/lettucecfd/lettuce.

Machine Learning Implicit Solvation for Molecular Dynamics

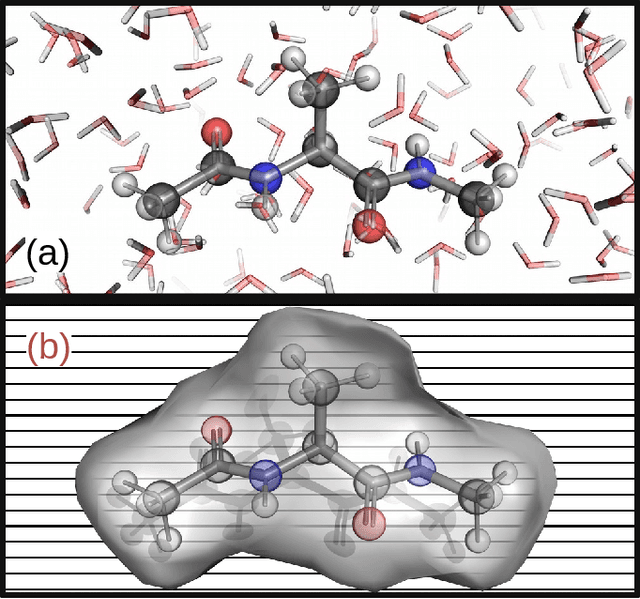
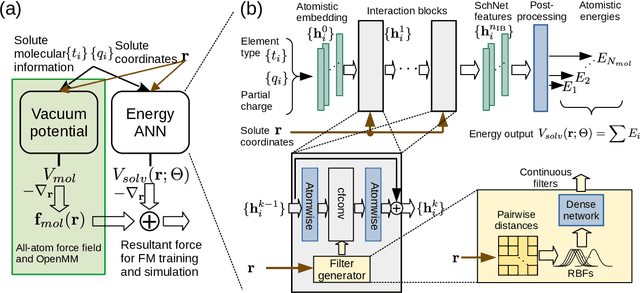
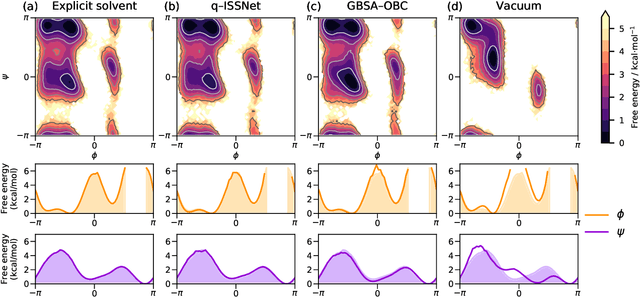
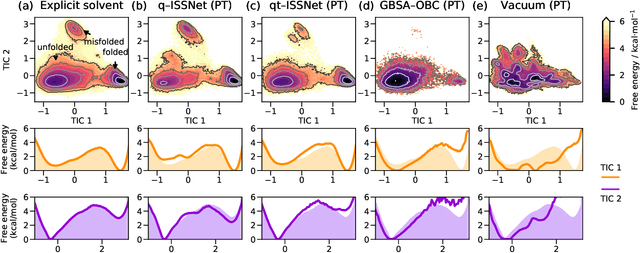
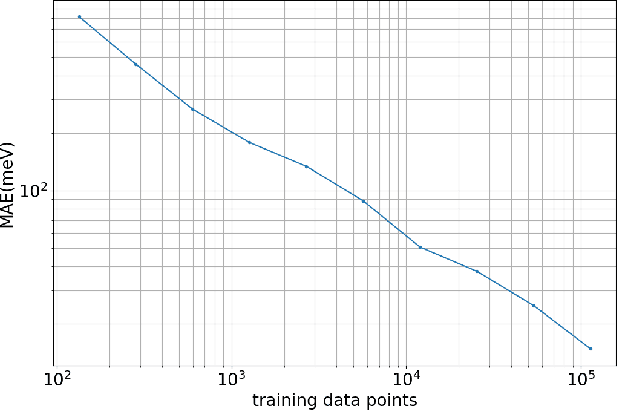
Accurate modeling of the solvent environment for biological molecules is crucial for computational biology and drug design. A popular approach to achieve long simulation time scales for large system sizes is to incorporate the effect of the solvent in a mean-field fashion with implicit solvent models. However, a challenge with existing implicit solvent models is that they often lack accuracy or certain physical properties compared to explicit solvent models, as the many-body effects of the neglected solvent molecules is difficult to model as a mean field. Here, we leverage machine learning (ML) and multi-scale coarse graining (CG) in order to learn implicit solvent models that can approximate the energetic and thermodynamic properties of a given explicit solvent model with arbitrary accuracy, given enough training data. Following the previous ML--CG models CGnet and CGSchnet, we introduce ISSNet, a graph neural network, to model the implicit solvent potential of mean force. ISSNet can learn from explicit solvent simulation data and be readily applied to MD simulations. We compare the solute conformational distributions under different solvation treatments for two peptide systems. The results indicate that ISSNet models can outperform widely-used generalized Born and surface area models in reproducing the thermodynamics of small protein systems with respect to explicit solvent. The success of this novel method demonstrates the potential benefit of applying machine learning methods in accurate modeling of solvent effects for in silico research and biomedical applications.

TorchMD: A deep learning framework for molecular simulations

Molecular dynamics simulations provide a mechanistic description of molecules by relying on empirical potentials. The quality and transferability of such potentials can be improved leveraging data-driven models derived with machine learning approaches. Here, we present TorchMD, a framework for molecular simulations with mixed classical and machine learning potentials. All of force computations including bond, angle, dihedral, Lennard-Jones and Coulomb interactions are expressed as PyTorch arrays and operations. Moreover, TorchMD enables learning and simulating neural network potentials. We validate it using standard Amber all-atom simulations, learning an ab-initio potential, performing an end-to-end training and finally learning and simulating a coarse-grained model for protein folding. We believe that TorchMD provides a useful tool-set to support molecular simulations of machine learning potentials. Code and data are freely available at \url{github.com/torchmd}.

Training Neural Networks with Property-Preserving Parameter Perturbations

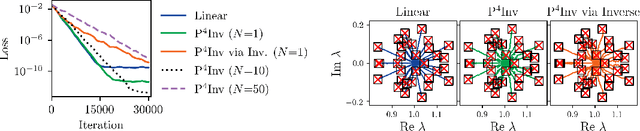
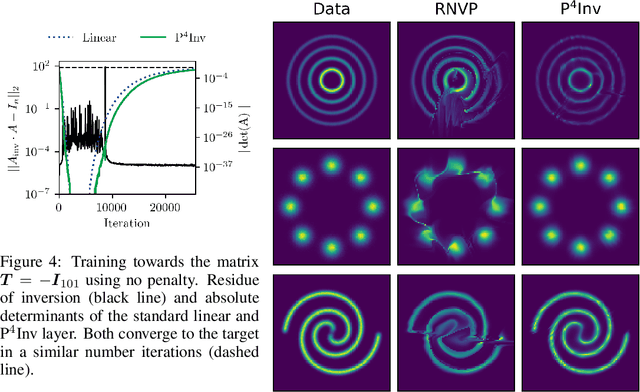
Many types of neural network layers rely on matrix properties such as invertibility or orthogonality. Retaining such properties during optimization with gradient-based stochastic optimizers is a challenging task, which is usually addressed by either reparameterization of the affected parameters or by directly optimizing on the manifold. In contrast, this work presents a novel, general approach of preserving matrix properties by using parameterized perturbations. In lieu of directly optimizing the network parameters, the introduced P$^{4}$ update optimizes perturbations and merges them into the actual parameters infrequently such that the desired property is preserved. As a demonstration, we use this concept to preserve invertibility of linear layers during training. This P$^{4}$Inv update allows keeping track of inverses and determinants via rank-one updates and without ever explicitly computing them. We show how such invertible blocks improve the mixing of coupling layers and thus the mode separation of the resulting normalizing flows.