Training Neural Networks with Property-Preserving Parameter Perturbations
Paper and Code
Oct 14, 2020
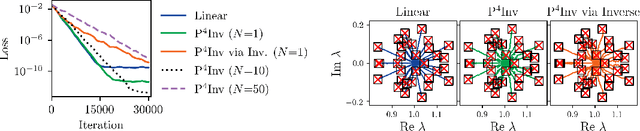

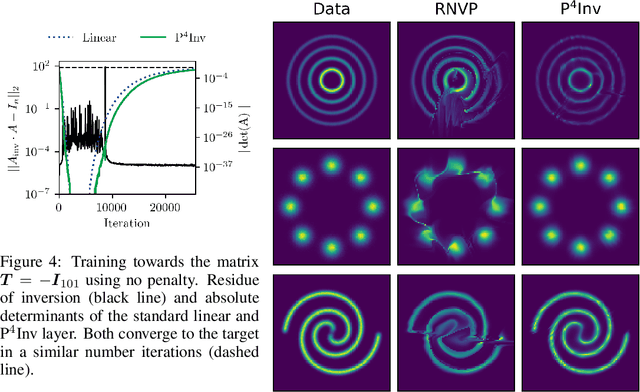
Many types of neural network layers rely on matrix properties such as invertibility or orthogonality. Retaining such properties during optimization with gradient-based stochastic optimizers is a challenging task, which is usually addressed by either reparameterization of the affected parameters or by directly optimizing on the manifold. In contrast, this work presents a novel, general approach of preserving matrix properties by using parameterized perturbations. In lieu of directly optimizing the network parameters, the introduced P$^{4}$ update optimizes perturbations and merges them into the actual parameters infrequently such that the desired property is preserved. As a demonstration, we use this concept to preserve invertibility of linear layers during training. This P$^{4}$Inv update allows keeping track of inverses and determinants via rank-one updates and without ever explicitly computing them. We show how such invertible blocks improve the mixing of coupling layers and thus the mode separation of the resulting normalizing flows.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge