Highly Accurate Real-space Electron Densities with Neural Networks

Variational ab-initio methods in quantum chemistry stand out among other methods in providing direct access to the wave function. This allows in principle straightforward extraction of any other observable of interest, besides the energy, but in practice this extraction is often technically difficult and computationally impractical. Here, we consider the electron density as a central observable in quantum chemistry and introduce a novel method to obtain accurate densities from real-space many-electron wave functions by representing the density with a neural network that captures known asymptotic properties and is trained from the wave function by score matching and noise-contrastive estimation. We use variational quantum Monte Carlo with deep-learning ans\"atze (deep QMC) to obtain highly accurate wave functions free of basis set errors, and from them, using our novel method, correspondingly accurate electron densities, which we demonstrate by calculating dipole moments, nuclear forces, contact densities, and other density-based properties.

Rigid body flows for sampling molecular crystal structures

Normalizing flows (NF) are a class of powerful generative models that have gained popularity in recent years due to their ability to model complex distributions with high flexibility and expressiveness. In this work, we introduce a new type of normalizing flow that is tailored for modeling positions and orientations of multiple objects in three-dimensional space, such as molecules in a crystal. Our approach is based on two key ideas: first, we define smooth and expressive flows on the group of unit quaternions, which allows us to capture the continuous rotational motion of rigid bodies; second, we use the double cover property of unit quaternions to define a proper density on the rotation group. This ensures that our model can be trained using standard likelihood-based methods or variational inference with respect to a thermodynamic target density. We evaluate the method by training Boltzmann generators for two molecular examples, namely the multi-modal density of a tetrahedral system in an external field and the ice XI phase in the TIP4P-Ew water model. Our flows can be combined with flows operating on the internal degrees of freedom of molecules, and constitute an important step towards the modeling of distributions of many interacting molecules.

Force-matching Coarse-Graining without Forces

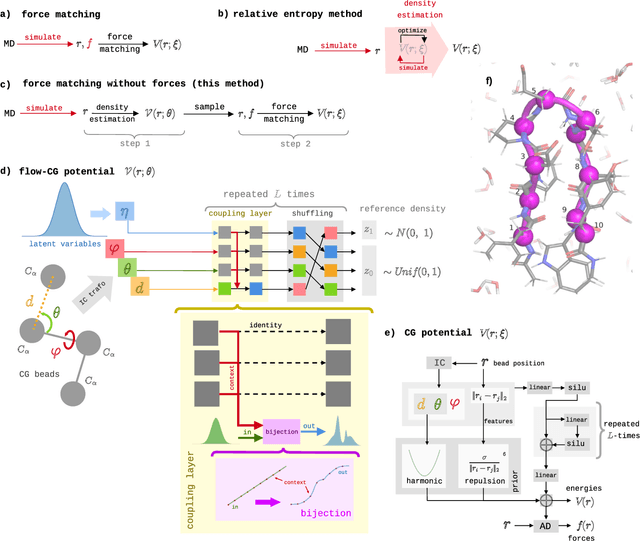
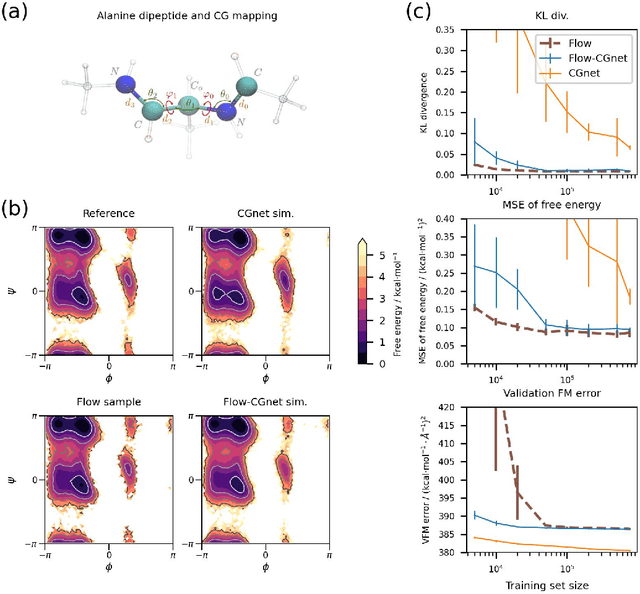
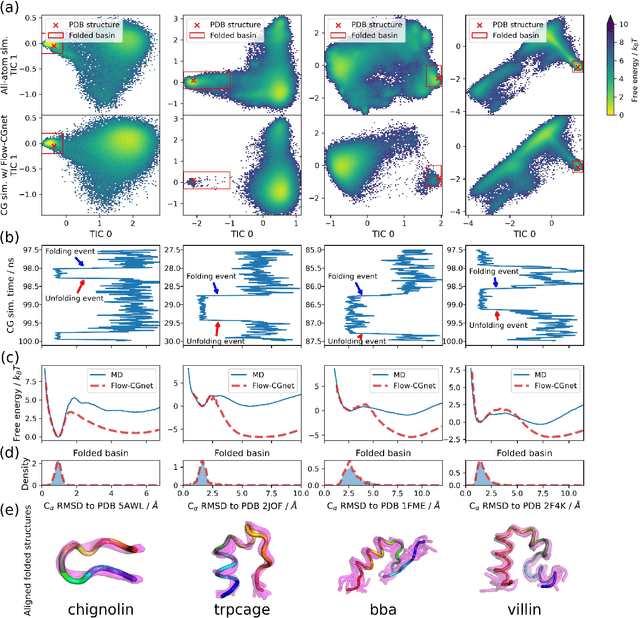
Coarse-grained (CG) molecular simulations have become a standard tool to study molecular processes on time-~and length-scales inaccessible to all-atom simulations. Learning CG force fields from all-atom data has mainly relied on force-matching and relative entropy minimization. Force-matching is straightforward to implement but requires the forces on the CG particles to be saved during all-atom simulation, and because these instantaneous forces depend on all degrees of freedom, they provide a very noisy signal that makes training the CG force field data inefficient. Relative entropy minimization does not require forces to be saved and is more data-efficient, but requires the CG model to be re-simulated during the iterative training procedure, which can make the training procedure extremely costly or lead to failure to converge. Here we present \emph{flow-matching}, a new training method for CG force fields that combines the advantages of force-matching and relative entropy minimization by leveraging normalizing flows, a generative deep learning method. Flow-matching first trains a normalizing flow to represent the CG probability density by using relative entropy minimization without suffering from the re-simulation problem because flows can directly sample from the equilibrium distribution they represent. Subsequently, the forces of the flow are used to train a CG force field by matching the coarse-grained forces directly, which is a much easier problem than traditional force-matching as it does not suffer from the noise problem. Besides not requiring forces, flow-matching also outperforms classical force-matching by an order of magnitude in terms of data efficiency and produces CG models that can capture the folding and unfolding of small proteins.

Smooth Normalizing Flows

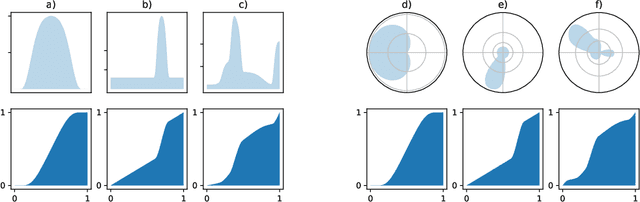
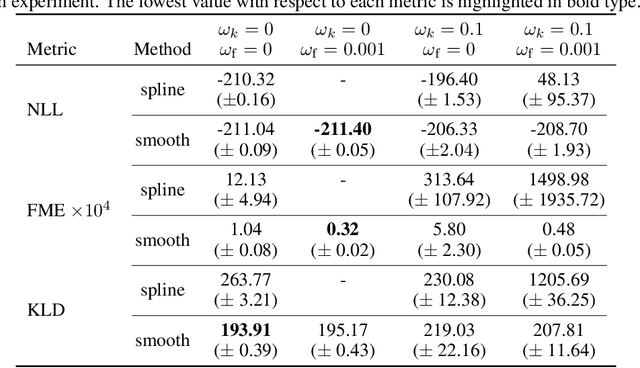
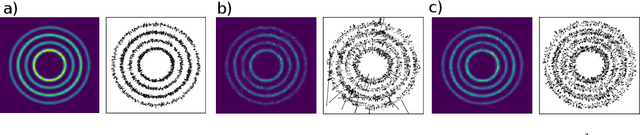
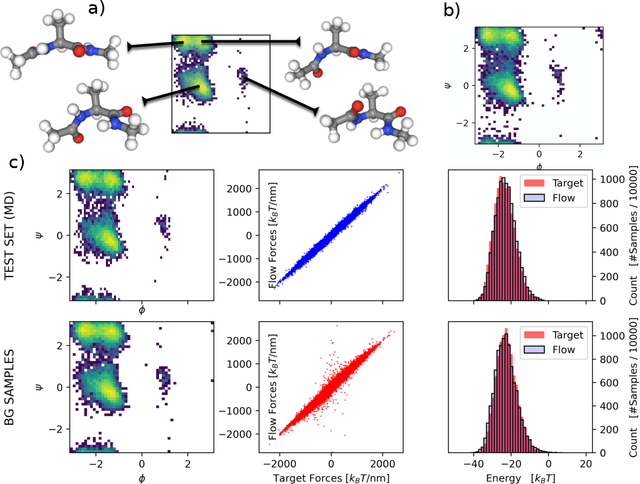
Normalizing flows are a promising tool for modeling probability distributions in physical systems. While state-of-the-art flows accurately approximate distributions and energies, applications in physics additionally require smooth energies to compute forces and higher-order derivatives. Furthermore, such densities are often defined on non-trivial topologies. A recent example are Boltzmann Generators for generating 3D-structures of peptides and small proteins. These generative models leverage the space of internal coordinates (dihedrals, angles, and bonds), which is a product of hypertori and compact intervals. In this work, we introduce a class of smooth mixture transformations working on both compact intervals and hypertori. Mixture transformations employ root-finding methods to invert them in practice, which has so far prevented bi-directional flow training. To this end, we show that parameter gradients and forces of such inverses can be computed from forward evaluations via the inverse function theorem. We demonstrate two advantages of such smooth flows: they allow training by force matching to simulation data and can be used as potentials in molecular dynamics simulations.

Generating stable molecules using imitation and reinforcement learning

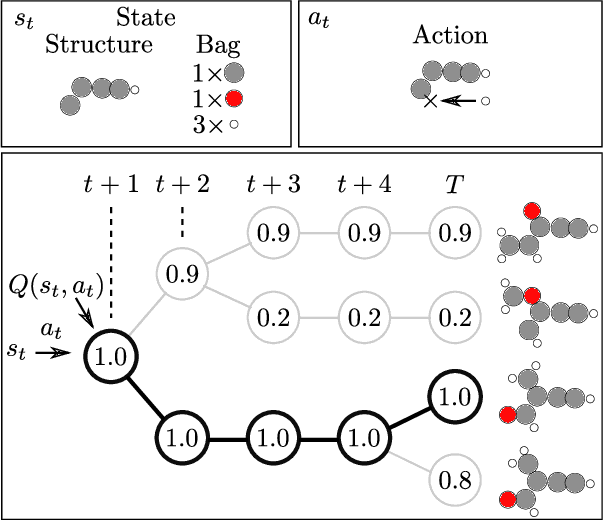
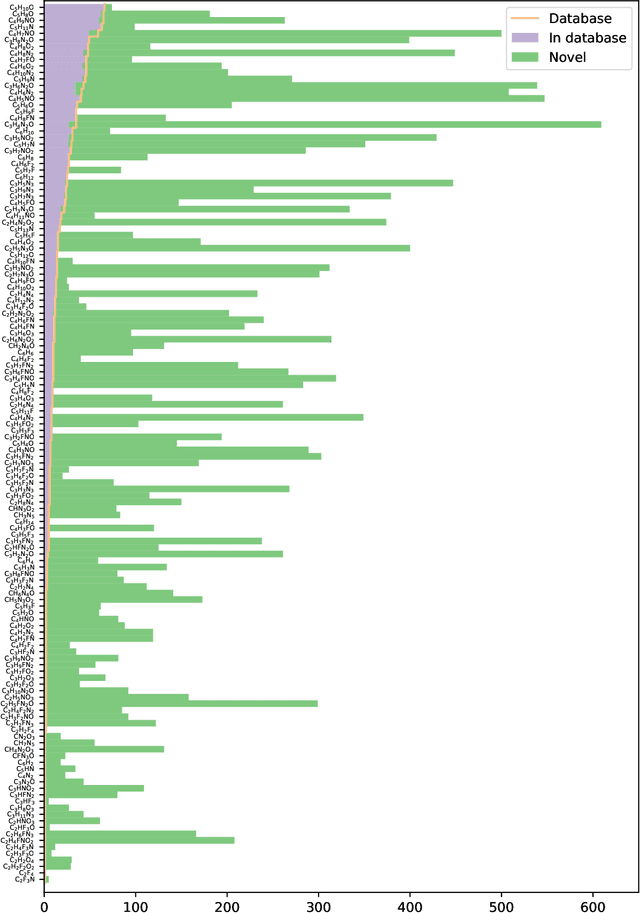
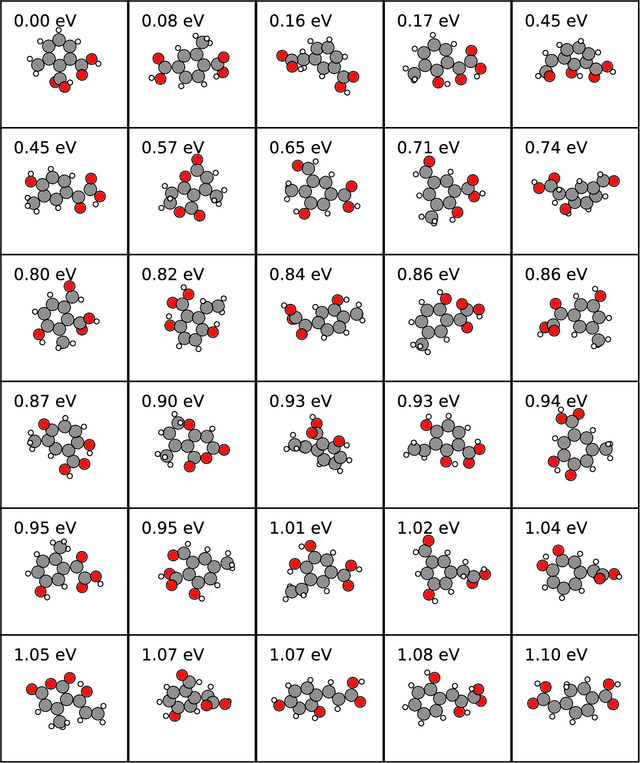
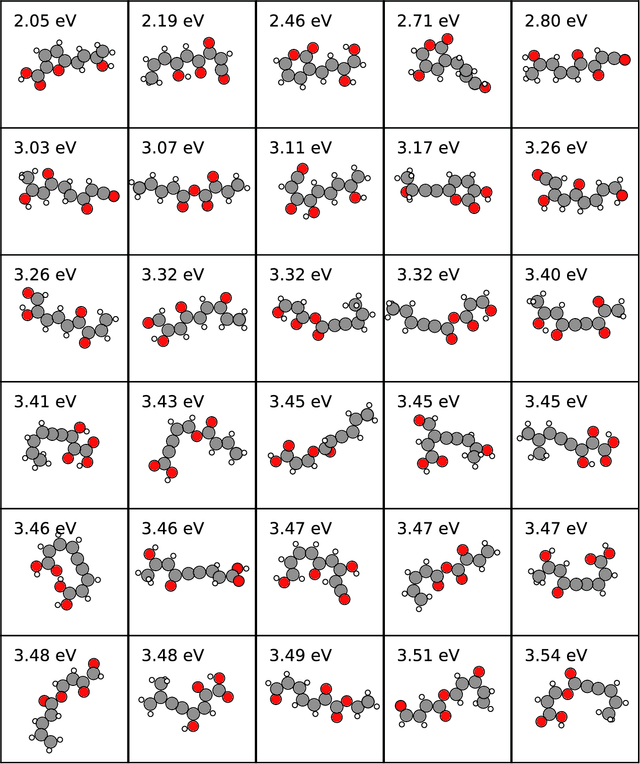
Chemical space is routinely explored by machine learning methods to discover interesting molecules, before time-consuming experimental synthesizing is attempted. However, these methods often rely on a graph representation, ignoring 3D information necessary for determining the stability of the molecules. We propose a reinforcement learning approach for generating molecules in cartesian coordinates allowing for quantum chemical prediction of the stability. To improve sample-efficiency we learn basic chemical rules from imitation learning on the GDB-11 database to create an initial model applicable for all stoichiometries. We then deploy multiple copies of the model conditioned on a specific stoichiometry in a reinforcement learning setting. The models correctly identify low energy molecules in the database and produce novel isomers not found in the training set. Finally, we apply the model to larger molecules to show how reinforcement learning further refines the imitation learning model in domains far from the training data.

Training Neural Networks with Property-Preserving Parameter Perturbations

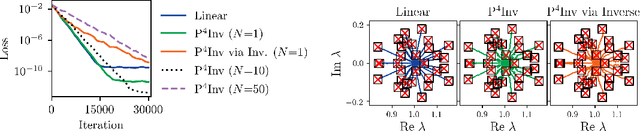
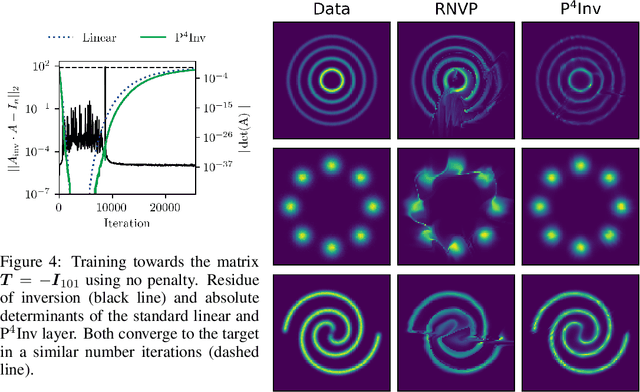
Many types of neural network layers rely on matrix properties such as invertibility or orthogonality. Retaining such properties during optimization with gradient-based stochastic optimizers is a challenging task, which is usually addressed by either reparameterization of the affected parameters or by directly optimizing on the manifold. In contrast, this work presents a novel, general approach of preserving matrix properties by using parameterized perturbations. In lieu of directly optimizing the network parameters, the introduced P$^{4}$ update optimizes perturbations and merges them into the actual parameters infrequently such that the desired property is preserved. As a demonstration, we use this concept to preserve invertibility of linear layers during training. This P$^{4}$Inv update allows keeping track of inverses and determinants via rank-one updates and without ever explicitly computing them. We show how such invertible blocks improve the mixing of coupling layers and thus the mode separation of the resulting normalizing flows.

Equivariant Flows: exact likelihood generative learning for symmetric densities

Normalizing flows are exact-likelihood generative neural networks which approximately transform samples from a simple prior distribution to samples of the probability distribution of interest. Recent work showed that such generative models can be utilized in statistical mechanics to sample equilibrium states of many-body systems in physics and chemistry. To scale and generalize these results, it is essential that the natural symmetries in the probability density - in physics defined by the invariances of the target potential - are built into the flow. We provide a theoretical sufficient criterion showing that the distribution generated by equivariant normalizing flows is invariant with respect to these symmetries by design. Furthermore, we propose building blocks for flows which preserve symmetries which are usually found in physical/chemical many-body particle systems. Using benchmark systems motivated from molecular physics, we demonstrate that those symmetry preserving flows can provide better generalization capabilities and sampling efficiency.

Stochastic Normalizing Flows

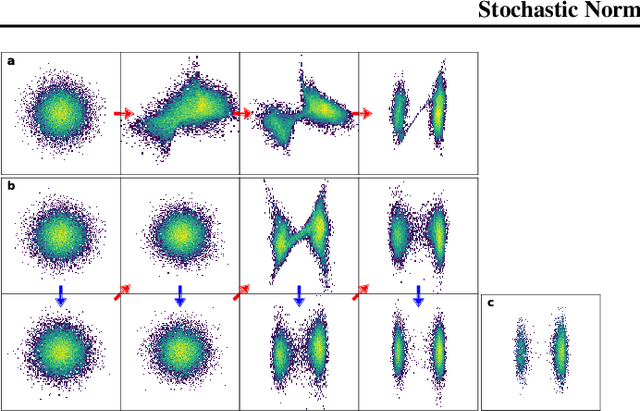
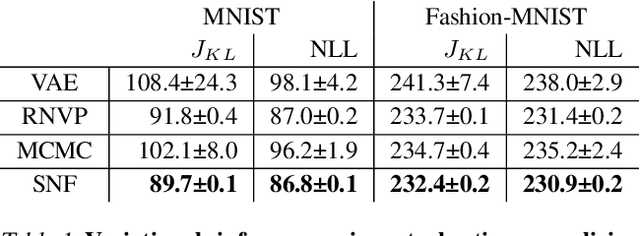
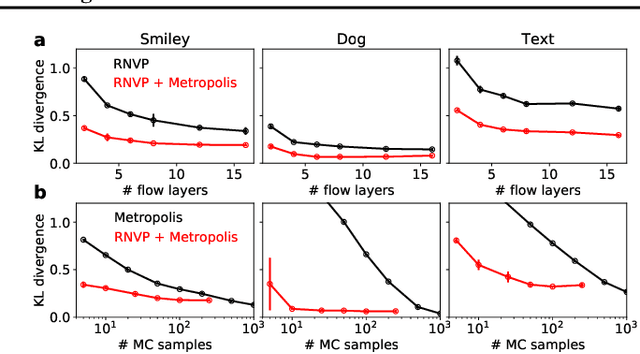
Normalizing flows are popular generative learning methods that train an invertible function to transform a simple prior distribution into a complicated target distribution. Here we generalize the framework by introducing Stochastic Normalizing Flows (SNF) - an arbitrary sequence of deterministic invertible functions and stochastic processes such as Markov Chain Monte Carlo (MCMC) or Langevin Dynamics. This combination can be powerful as adding stochasticity to a flow helps overcoming expressiveness limitations of a chosen deterministic invertible function, while the trainable flow transformations can improve the sampling efficiency over pure MCMC. Key to our approach is that we can match a marginal target density without having to marginalize out the stochasticity of traversed paths. Invoking ideas from nonequilibrium statistical mechanics, we introduce a training method that only uses conditional path probabilities. We can turn an SNF into a Boltzmann Generator that samples asymptotically unbiased from a given target density by importance sampling of these paths. We illustrate the representational power, sampling efficiency and asymptotic correctness of SNFs on several benchmarks.

DP-MAC: The Differentially Private Method of Auxiliary Coordinates for Deep Learning

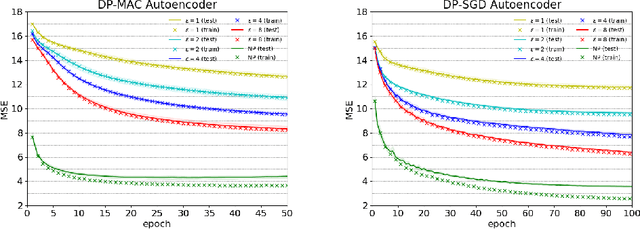
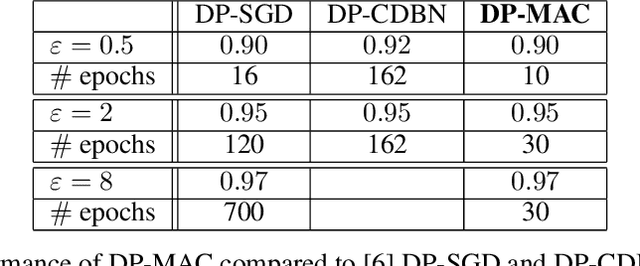
Developing a differentially private deep learning algorithm is challenging, due to the difficulty in analyzing the sensitivity of objective functions that are typically used to train deep neural networks. Many existing methods resort to the stochastic gradient descent algorithm and apply a pre-defined sensitivity to the gradients for privatizing weights. However, their slow convergence typically yields a high cumulative privacy loss. Here, we take a different route by employing the method of auxiliary coordinates, which allows us to independently update the weights per layer by optimizing a per-layer objective function. This objective function can be well approximated by a low-order Taylor's expansion, in which sensitivity analysis becomes tractable. We perturb the coefficients of the expansion for privacy, which we optimize using more advanced optimization routines than SGD for faster convergence. We empirically show that our algorithm provides a decent trained model quality under a modest privacy budget.

Equivariant Flows: sampling configurations for multi-body systems with symmetric energies

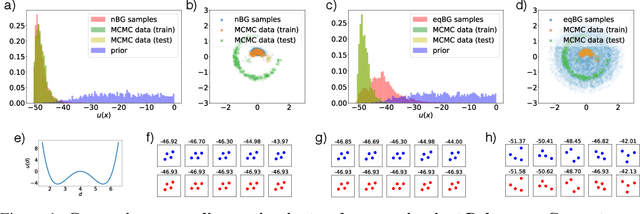
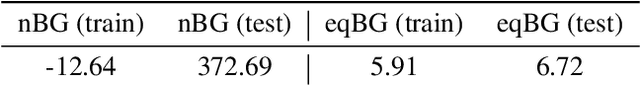
Flows are exact-likelihood generative neural networks that transform samples from a simple prior distribution to the samples of the probability distribution of interest. Boltzmann Generators (BG) combine flows and statistical mechanics to sample equilibrium states of strongly interacting many-body systems such as proteins with 1000 atoms. In order to scale and generalize these results, it is essential that the natural symmetries of the probability density - in physics defined by the invariances of the energy function - are built into the flow. Here we develop theoretical tools for constructing such equivariant flows and demonstrate that a BG that is equivariant with respect to rotations and particle permutations can generalize to sampling nontrivially new configurations where a nonequivariant BG cannot.