Pre-Pruning and Gradient-Dropping Improve Differentially Private Image Classification

Scalability is a significant challenge when it comes to applying differential privacy to training deep neural networks. The commonly used DP-SGD algorithm struggles to maintain a high level of privacy protection while achieving high accuracy on even moderately sized models. To tackle this challenge, we take advantage of the fact that neural networks are overparameterized, which allows us to improve neural network training with differential privacy. Specifically, we introduce a new training paradigm that uses \textit{pre-pruning} and \textit{gradient-dropping} to reduce the parameter space and improve scalability. The process starts with pre-pruning the parameters of the original network to obtain a smaller model that is then trained with DP-SGD. During training, less important gradients are dropped, and only selected gradients are updated. Our training paradigm introduces a tension between the rates of pre-pruning and gradient-dropping, privacy loss, and classification accuracy. Too much pre-pruning and gradient-dropping reduces the model's capacity and worsens accuracy, while training a smaller model requires less privacy budget for achieving good accuracy. We evaluate the interplay between these factors and demonstrate the effectiveness of our training paradigm for both training from scratch and fine-tuning pre-trained networks on several benchmark image classification datasets. The tools can also be readily incorporated into existing training paradigms.

Differentially Private Latent Diffusion Models

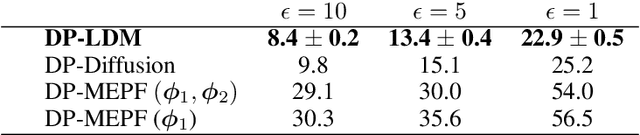
Diffusion models (DMs) are widely used for generating high-quality image datasets. However, since they operate directly in the high-dimensional pixel space, optimization of DMs is computationally expensive, requiring long training times. This contributes to large amounts of noise being injected into the differentially private learning process, due to the composability property of differential privacy. To address this challenge, we propose training Latent Diffusion Models (LDMs) with differential privacy. LDMs use powerful pre-trained autoencoders to reduce the high-dimensional pixel space to a much lower-dimensional latent space, making training DMs more efficient and fast. Unlike [Ghalebikesabi et al., 2023] that pre-trains DMs with public data then fine-tunes them with private data, we fine-tune only the attention modules of LDMs at varying layers with privacy-sensitive data, reducing the number of trainable parameters by approximately 96% compared to fine-tuning the entire DM. We test our algorithm on several public-private data pairs, such as ImageNet as public data and CIFAR10 and CelebA as private data, and SVHN as public data and MNIST as private data. Our approach provides a promising direction for training more powerful, yet training-efficient differentially private DMs that can produce high-quality synthetic images.

Differential Privacy Meets Neural Network Pruning

A major challenge in applying differential privacy to training deep neural network models is scalability.The widely-used training algorithm, differentially private stochastic gradient descent (DP-SGD), struggles with training moderately-sized neural network models for a value of epsilon corresponding to a high level of privacy protection. In this paper, we explore the idea of dimensionality reduction inspired by neural network pruning to improve the scalability of DP-SGD. We study the interplay between neural network pruning and differential privacy, through the two modes of parameter updates. We call the first mode, parameter freezing, where we pre-prune the network and only update the remaining parameters using DP-SGD. We call the second mode, parameter selection, where we select which parameters to update at each step of training and update only those selected using DP-SGD. In these modes, we use public data for freezing or selecting parameters to avoid privacy loss incurring in these steps. Naturally, the closeness between the private and public data plays an important role in the success of this paradigm. Our experimental results demonstrate how decreasing the parameter space improves differentially private training. Moreover, by studying two popular forms of pruning which do not rely on gradients and do not incur an additional privacy loss, we show that random selection performs on par with magnitude-based selection when it comes to DP-SGD training.

Differentially Private Neural Tangent Kernels for Privacy-Preserving Data Generation

Maximum mean discrepancy (MMD) is a particularly useful distance metric for differentially private data generation: when used with finite-dimensional features it allows us to summarize and privatize the data distribution once, which we can repeatedly use during generator training without further privacy loss. An important question in this framework is, then, what features are useful to distinguish between real and synthetic data distributions, and whether those enable us to generate quality synthetic data. This work considers the using the features of $\textit{neural tangent kernels (NTKs)}$, more precisely $\textit{empirical}$ NTKs (e-NTKs). We find that, perhaps surprisingly, the expressiveness of the untrained e-NTK features is comparable to that of the features taken from pre-trained perceptual features using public data. As a result, our method improves the privacy-accuracy trade-off compared to other state-of-the-art methods, without relying on any public data, as demonstrated on several tabular and image benchmark datasets.

Differentially Private Data Generation Needs Better Features

Training even moderately-sized generative models with differentially-private stochastic gradient descent (DP-SGD) is difficult: the required level of noise for reasonable levels of privacy is simply too large. We advocate instead building off a good, relevant representation on public data, then using private data only for "transfer learning." In particular, we minimize the maximum mean discrepancy (MMD) between private target data and the generated distribution, using a kernel based on perceptual features from a public dataset. With the MMD, we can simply privatize the data-dependent term once and for all, rather than introducing noise at each step of optimization as in DP-SGD. Our algorithm allows us to generate CIFAR10-level images faithfully with $\varepsilon \approx 2$, far surpassing the current state of the art, which only models MNIST and FashionMNIST at $\varepsilon \approx 10$. Our work introduces simple yet powerful foundations for reducing the gap between private and non-private deep generative models.

DP-SEP! Differentially Private Stochastic Expectation Propagation

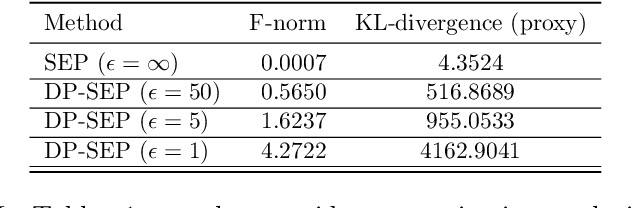
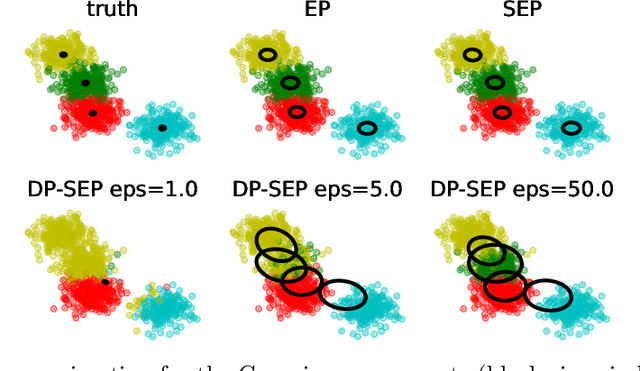
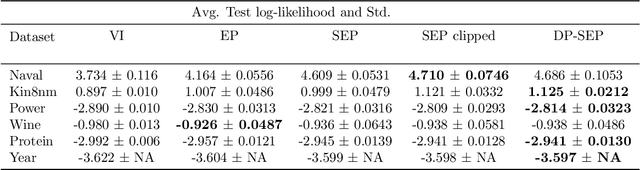
We are interested in privatizing an approximate posterior inference algorithm called Expectation Propagation (EP). EP approximates the posterior by iteratively refining approximations to the local likelihoods, and is known to provide better posterior uncertainties than those by variational inference (VI). However, using EP for large-scale datasets imposes a challenge in terms of memory requirements as it needs to maintain each of the local approximates in memory. To overcome this problem, stochastic expectation propagation (SEP) was proposed, which only considers a unique local factor that captures the average effect of each likelihood term to the posterior and refines it in a way analogous to EP. In terms of privacy, SEP is more tractable than EP because at each refining step of a factor, the remaining factors are fixed to the same value and do not depend on other datapoints as in EP, which makes the sensitivity analysis tractable. We provide a theoretical analysis of the privacy-accuracy trade-off in the posterior estimates under differentially private stochastic expectation propagation (DP-SEP). Furthermore, we demonstrate the performance of our DP-SEP algorithm evaluated on both synthetic and real-world datasets in terms of the quality of posterior estimates at different levels of guaranteed privacy.

Polynomial magic! Hermite polynomials for private data generation

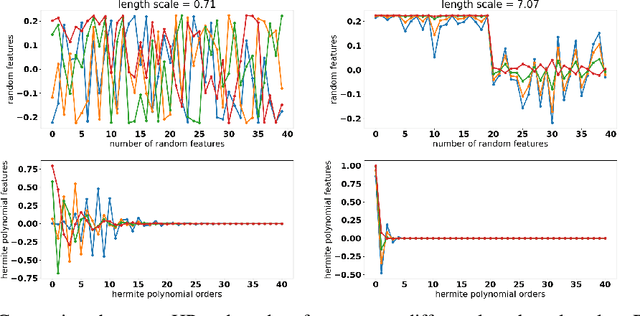
Kernel mean embedding is a useful tool to compare probability measures. Despite its usefulness, kernel mean embedding considers infinite-dimensional features, which are challenging to handle in the context of differentially private data generation. A recent work proposes to approximate the kernel mean embedding of data distribution using finite-dimensional random features, where the sensitivity of the features becomes analytically tractable. More importantly, this approach significantly reduces the privacy cost, compared to other known privatization methods (e.g., DP-SGD), as the approximate kernel mean embedding of the data distribution is privatized only once and can then be repeatedly used during training of a generator without incurring any further privacy cost. However, the required number of random features is excessively high, often ten thousand to a hundred thousand, which worsens the sensitivity of the approximate kernel mean embedding. To improve the sensitivity, we propose to replace random features with Hermite polynomial features. Unlike the random features, the Hermite polynomial features are ordered, where the features at the low orders contain more information on the distribution than those at the high orders. Hence, a relatively low order of Hermite polynomial features can more accurately approximate the mean embedding of the data distribution compared to a significantly higher number of random features. As a result, using the Hermite polynomial features, we significantly improve the privacy-accuracy trade-off, reflected in the high quality and diversity of the generated data, when tested on several heterogeneous tabular datasets, as well as several image benchmark datasets.

Dirichlet Pruning for Neural Network Compression

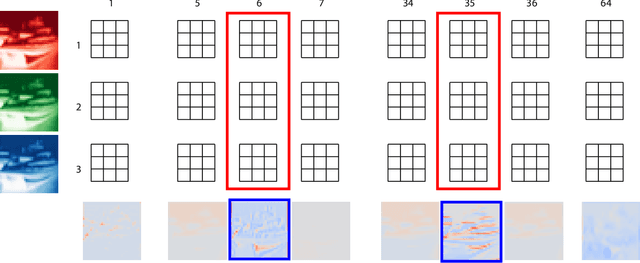
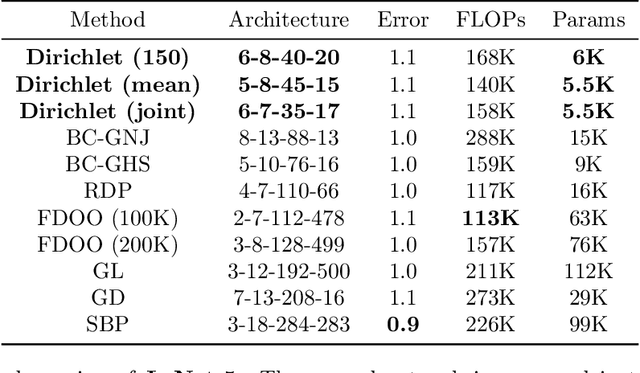
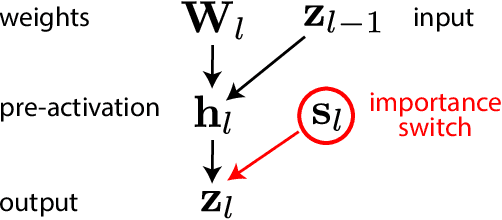
We introduce Dirichlet pruning, a novel post-processing technique to transform a large neural network model into a compressed one. Dirichlet pruning is a form of structured pruning which assigns the Dirichlet distribution over each layer's channels in convolutional layers (or neurons in fully-connected layers), and estimates the parameters of the distribution over these units using variational inference. The learned distribution allows us to remove unimportant units, resulting in a compact architecture containing only crucial features for a task at hand. Our method is extremely fast to train. The number of newly introduced Dirichlet parameters is only linear in the number of channels, which allows for rapid training, requiring as little as one epoch to converge. We perform extensive experiments, in particular on larger architectures such as VGG and WideResNet (45% and 52% compression rate, respectively) where our method achieves the state-of-the-art compression performance and provides interpretable features as a by-product.

Q-FIT: The Quantifiable Feature Importance Technique for Explainable Machine Learning

We introduce a novel framework to quantify the importance of each input feature for model explainability. A user of our framework can choose between two modes: (a) global explanation: providing feature importance globally across all the data points; and (b) local explanation: providing feature importance locally for each individual data point. The core idea of our method comes from utilizing the Dirichlet distribution to define a distribution over the importance of input features. This particular distribution is useful in ranking the importance of the input features as a sample from this distribution is a probability vector (i.e., the vector components sum to 1), Thus, the ranking uncovered by our framework which provides a \textit{quantifiable explanation} of how significant each input feature is to a model's output. This quantifiable explainability differentiates our method from existing feature-selection methods, which simply determine whether a feature is relevant or not. Furthermore, a distribution over the explanation allows to define a closed-form divergence to measure the similarity between learned feature importance under different models. We use this divergence to study how the feature importance trade-offs with essential notions in modern machine learning, such as privacy and fairness. We show the effectiveness of our method on a variety of synthetic and real datasets, taking into account both tabular and image datasets.