Maximum Mean Discrepancy with Unequal Sample Sizes via Generalized U-Statistics

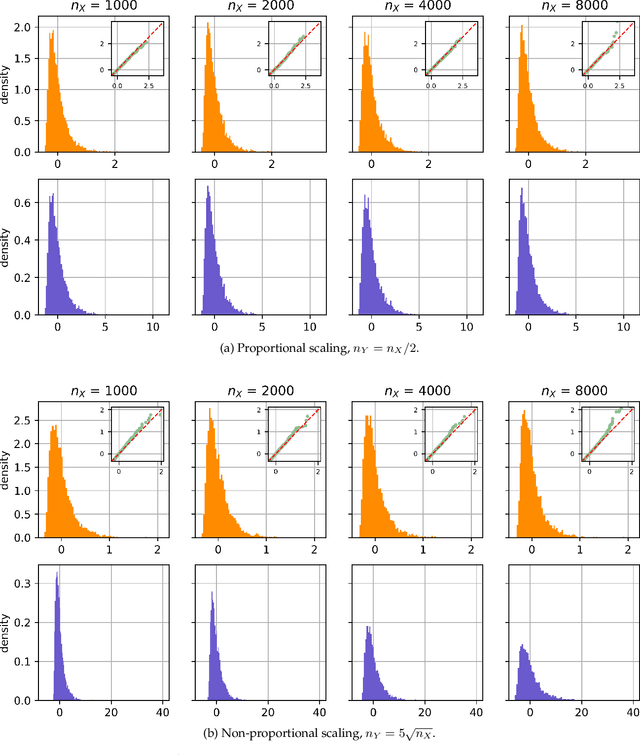
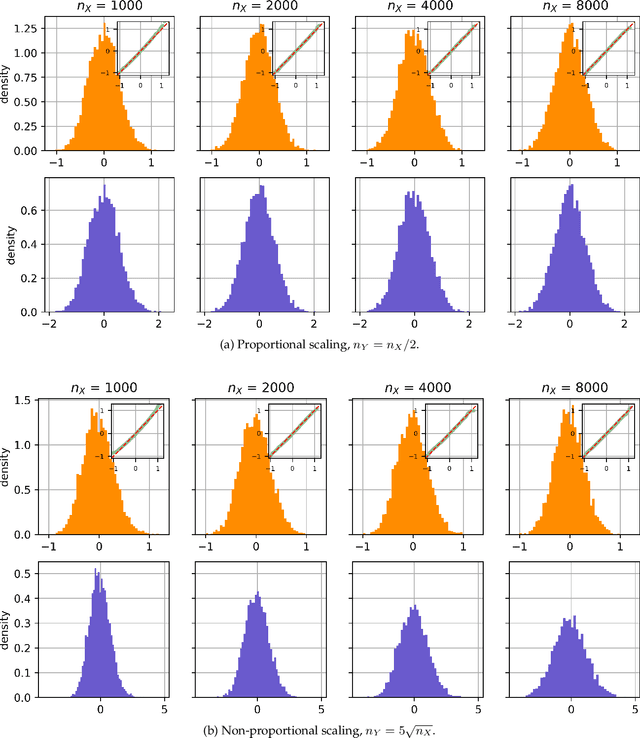
Existing two-sample testing techniques, particularly those based on choosing a kernel for the Maximum Mean Discrepancy (MMD), often assume equal sample sizes from the two distributions. Applying these methods in practice can require discarding valuable data, unnecessarily reducing test power. We address this long-standing limitation by extending the theory of generalized U-statistics and applying it to the usual MMD estimator, resulting in new characterization of the asymptotic distributions of the MMD estimator with unequal sample sizes (particularly outside the proportional regimes required by previous partial results). This generalization also provides a new criterion for optimizing the power of an MMD test with unequal sample sizes. Our approach preserves all available data, enhancing test accuracy and applicability in realistic settings. Along the way, we give much cleaner characterizations of the variance of MMD estimators, revealing something that might be surprising to those in the area: while zero MMD implies a degenerate estimator, it is sometimes possible to have a degenerate estimator with nonzero MMD as well; we give a construction and a proof that it does not happen in common situations.

On the Hardness of Conditional Independence Testing In Practice

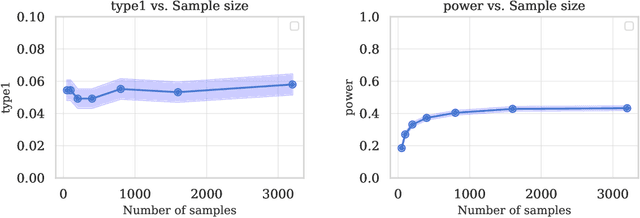
Tests of conditional independence (CI) underpin a number of important problems in machine learning and statistics, from causal discovery to evaluation of predictor fairness and out-of-distribution robustness. Shah and Peters (2020) showed that, contrary to the unconditional case, no universally finite-sample valid test can ever achieve nontrivial power. While informative, this result (based on "hiding" dependence) does not seem to explain the frequent practical failures observed with popular CI tests. We investigate the Kernel-based Conditional Independence (KCI) test - of which we show the Generalized Covariance Measure underlying many recent tests is nearly a special case - and identify the major factors underlying its practical behavior. We highlight the key role of errors in the conditional mean embedding estimate for the Type-I error, while pointing out the importance of selecting an appropriate conditioning kernel (not recognized in previous work) as being necessary for good test power but also tending to inflate Type-I error.

Efficient kernelized bandit algorithms via exploration distributions

We consider a kernelized bandit problem with a compact arm set ${X} \subset \mathbb{R}^d $ and a fixed but unknown reward function $f^*$ with a finite norm in some Reproducing Kernel Hilbert Space (RKHS). We propose a class of computationally efficient kernelized bandit algorithms, which we call GP-Generic, based on a novel concept: exploration distributions. This class of algorithms includes Upper Confidence Bound-based approaches as a special case, but also allows for a variety of randomized algorithms. With careful choice of exploration distribution, our proposed generic algorithm realizes a wide range of concrete algorithms that achieve $\tilde{O}(\gamma_T\sqrt{T})$ regret bounds, where $\gamma_T$ characterizes the RKHS complexity. This matches known results for UCB- and Thompson Sampling-based algorithms; we also show that in practice, randomization can yield better practical results.

On the Effect of Negative Gradient in Group Relative Deep Reinforcement Optimization

Reinforcement learning (RL) has become popular in enhancing the reasoning capabilities of large language models (LLMs), with Group Relative Policy Optimization (GRPO) emerging as a widely used algorithm in recent systems. Despite GRPO's widespread adoption, we identify a previously unrecognized phenomenon we term Lazy Likelihood Displacement (LLD), wherein the likelihood of correct responses marginally increases or even decreases during training. This behavior mirrors a recently discovered misalignment issue in Direct Preference Optimization (DPO), attributed to the influence of negative gradients. We provide a theoretical analysis of GRPO's learning dynamic, identifying the source of LLD as the naive penalization of all tokens in incorrect responses with the same strength. To address this, we develop a method called NTHR, which downweights penalties on tokens contributing to the LLD. Unlike prior DPO-based approaches, NTHR takes advantage of GRPO's group-based structure, using correct responses as anchors to identify influential tokens. Experiments on math reasoning benchmarks demonstrate that NTHR effectively mitigates LLD, yielding consistent performance gains across models ranging from 0.5B to 3B parameters.

Uncertainty Herding: One Active Learning Method for All Label Budgets

Most active learning research has focused on methods which perform well when many labels are available, but can be dramatically worse than random selection when label budgets are small. Other methods have focused on the low-budget regime, but do poorly as label budgets increase. As the line between "low" and "high" budgets varies by problem, this is a serious issue in practice. We propose uncertainty coverage, an objective which generalizes a variety of low- and high-budget objectives, as well as natural, hyperparameter-light methods to smoothly interpolate between low- and high-budget regimes. We call greedy optimization of the estimate Uncertainty Herding; this simple method is computationally fast, and we prove that it nearly optimizes the distribution-level coverage. In experimental validation across a variety of active learning tasks, our proposal matches or beats state-of-the-art performance in essentially all cases; it is the only method of which we are aware that reliably works well in both low- and high-budget settings.

Understanding Simplicity Bias towards Compositional Mappings via Learning Dynamics

Obtaining compositional mappings is important for the model to generalize well compositionally. To better understand when and how to encourage the model to learn such mappings, we study their uniqueness through different perspectives. Specifically, we first show that the compositional mappings are the simplest bijections through the lens of coding length (i.e., an upper bound of their Kolmogorov complexity). This property explains why models having such mappings can generalize well. We further show that the simplicity bias is usually an intrinsic property of neural network training via gradient descent. That partially explains why some models spontaneously generalize well when they are trained appropriately.

Learning Deep Kernels for Non-Parametric Independence Testing

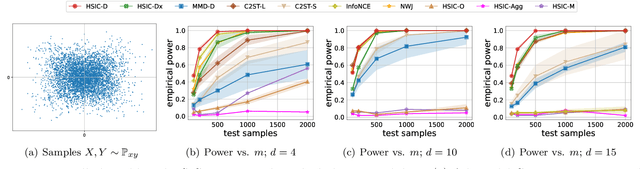
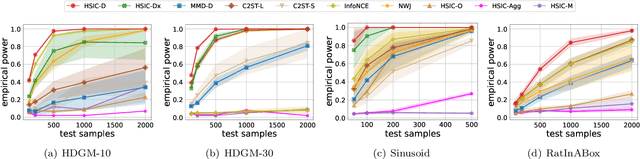
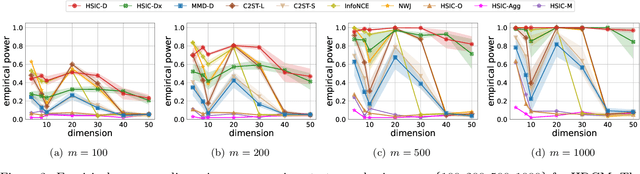
The Hilbert-Schmidt Independence Criterion (HSIC) is a powerful tool for nonparametric detection of dependence between random variables. It crucially depends, however, on the selection of reasonable kernels; commonly-used choices like the Gaussian kernel, or the kernel that yields the distance covariance, are sufficient only for amply sized samples from data distributions with relatively simple forms of dependence. We propose a scheme for selecting the kernels used in an HSIC-based independence test, based on maximizing an estimate of the asymptotic test power. We prove that maximizing this estimate indeed approximately maximizes the true power of the test, and demonstrate that our learned kernels can identify forms of structured dependence between random variables in various experiments.

Why Do You Grok? A Theoretical Analysis of Grokking Modular Addition

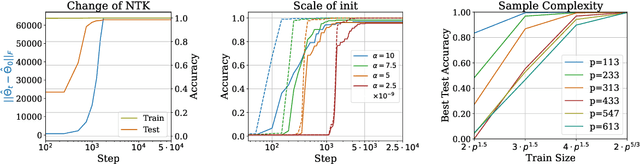
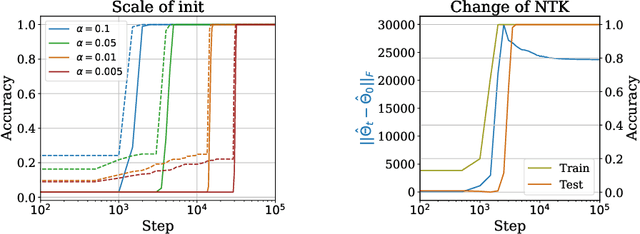
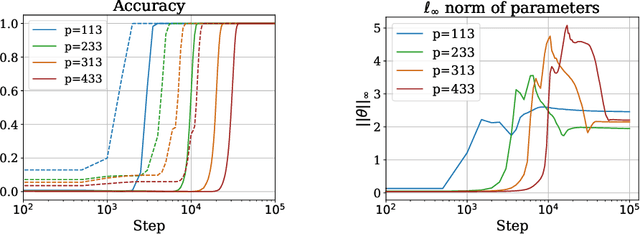
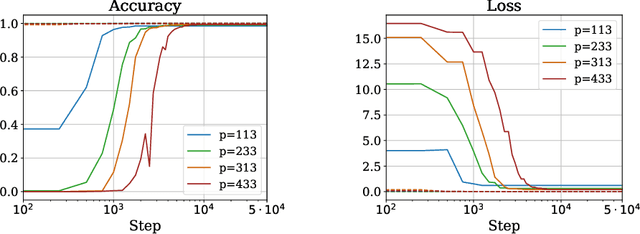
We present a theoretical explanation of the ``grokking'' phenomenon, where a model generalizes long after overfitting,for the originally-studied problem of modular addition. First, we show that early in gradient descent, when the ``kernel regime'' approximately holds, no permutation-equivariant model can achieve small population error on modular addition unless it sees at least a constant fraction of all possible data points. Eventually, however, models escape the kernel regime. We show that two-layer quadratic networks that achieve zero training loss with bounded $\ell_{\infty}$ norm generalize well with substantially fewer training points, and further show such networks exist and can be found by gradient descent with small $\ell_{\infty}$ regularization. We further provide empirical evidence that these networks as well as simple Transformers, leave the kernel regime only after initially overfitting. Taken together, our results strongly support the case for grokking as a consequence of the transition from kernel-like behavior to limiting behavior of gradient descent on deep networks.

Generalized Coverage for More Robust Low-Budget Active Learning

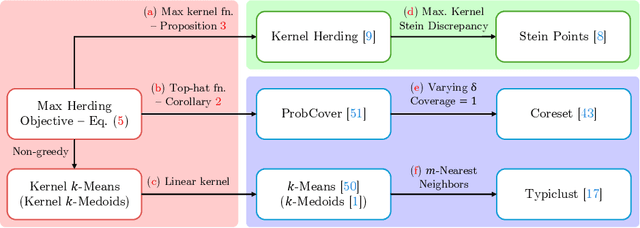
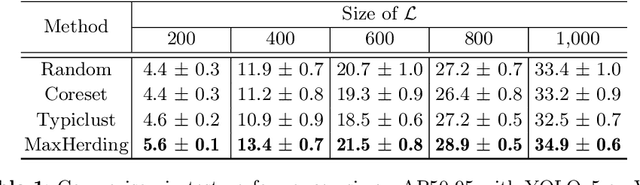
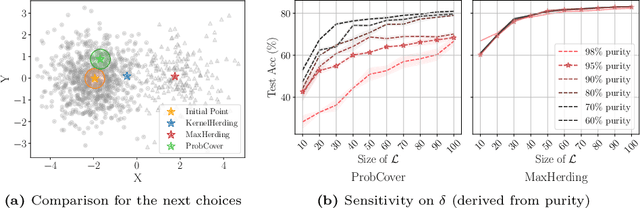
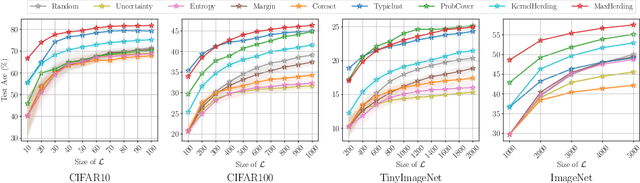
The ProbCover method of Yehuda et al. is a well-motivated algorithm for active learning in low-budget regimes, which attempts to "cover" the data distribution with balls of a given radius at selected data points. We demonstrate, however, that the performance of this algorithm is extremely sensitive to the choice of this radius hyper-parameter, and that tuning it is quite difficult, with the original heuristic frequently failing. We thus introduce (and theoretically motivate) a generalized notion of "coverage," including ProbCover's objective as a special case, but also allowing smoother notions that are far more robust to hyper-parameter choice. We propose an efficient greedy method to optimize this coverage, generalizing ProbCover's algorithm; due to its close connection to kernel herding, we call it "MaxHerding." The objective can also be optimized non-greedily through a variant of $k$-medoids, clarifying the relationship to other low-budget active learning methods. In comprehensive experiments, MaxHerding surpasses existing active learning methods across multiple low-budget image classification benchmarks, and does so with less computational cost than most competitive methods.

Learning Dynamics of LLM Finetuning

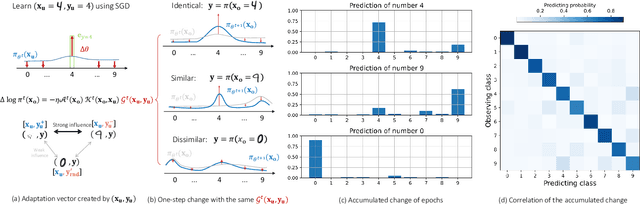
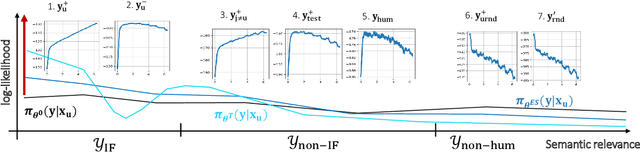
Learning dynamics, which describes how the learning of specific training examples influences the model's prediction of other examples, give us a powerful tool for understanding the behavior of deep learning systems. We study the learning dynamics of large language models during finetuning, by analyzing the step-wise decomposition and accumulated influence among different responses. Our framework allows a uniform interpretation of many interesting observations about the training of popular algorithms for both instruction tuning and preference tuning. The analysis not only explains where the benefits of these methods come from but also inspires a simple, effective method to further improve the alignment performance. Code for experiments is available at https://github.com/Joshua-Ren/Learning_dynamics_LLM.