Why Do You Grok? A Theoretical Analysis of Grokking Modular Addition
Paper and Code
Jul 17, 2024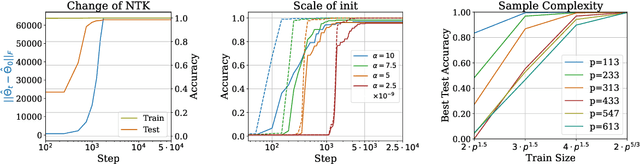
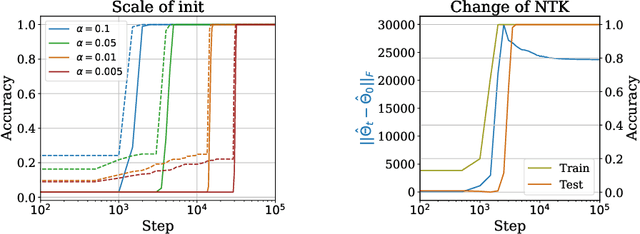
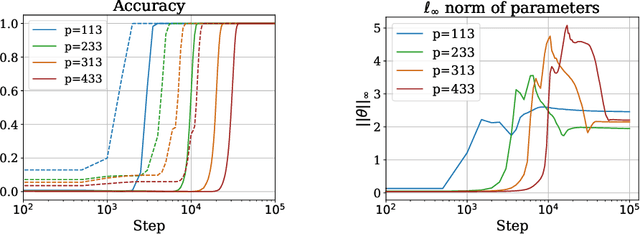
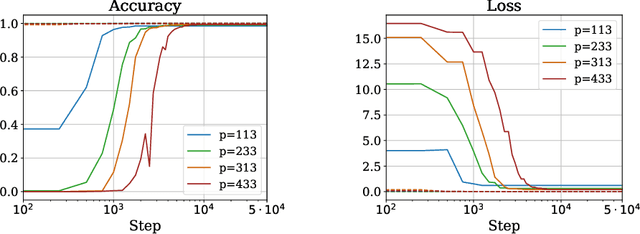
We present a theoretical explanation of the ``grokking'' phenomenon, where a model generalizes long after overfitting,for the originally-studied problem of modular addition. First, we show that early in gradient descent, when the ``kernel regime'' approximately holds, no permutation-equivariant model can achieve small population error on modular addition unless it sees at least a constant fraction of all possible data points. Eventually, however, models escape the kernel regime. We show that two-layer quadratic networks that achieve zero training loss with bounded $\ell_{\infty}$ norm generalize well with substantially fewer training points, and further show such networks exist and can be found by gradient descent with small $\ell_{\infty}$ regularization. We further provide empirical evidence that these networks as well as simple Transformers, leave the kernel regime only after initially overfitting. Taken together, our results strongly support the case for grokking as a consequence of the transition from kernel-like behavior to limiting behavior of gradient descent on deep networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge