Adam Exploits $\ell_\infty$-geometry of Loss Landscape via Coordinate-wise Adaptivity

Adam outperforms SGD when training language models. Yet this advantage is not well-understood theoretically -- previous convergence analysis for Adam and SGD mainly focuses on the number of steps $T$ and is already minimax-optimal in non-convex cases, which are both $\widetilde{O}(T^{-1/4})$. In this work, we argue that the exploitation of nice $\ell_\infty$-geometry is the key advantage of Adam over SGD. More specifically, we give a new convergence analysis for Adam under novel assumptions that loss is smooth under $\ell_\infty$-geometry rather than the more common $\ell_2$-geometry, which yields a much better empirical smoothness constant for GPT-2 and ResNet models. Our experiments confirm that Adam performs much worse when the favorable $\ell_\infty$-geometry is changed while SGD provably remains unaffected. We also extend the convergence analysis to blockwise Adam under novel blockwise smoothness assumptions.

Why Do You Grok? A Theoretical Analysis of Grokking Modular Addition

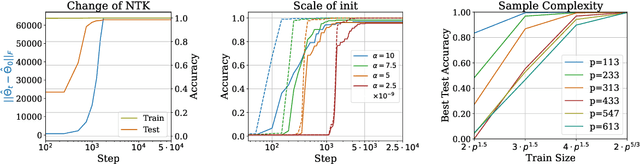
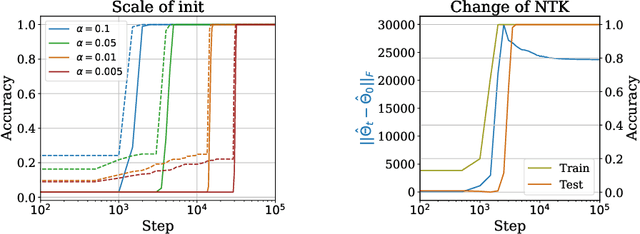
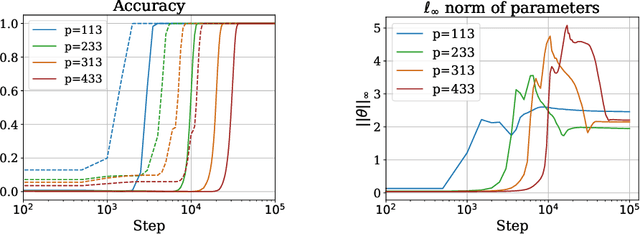
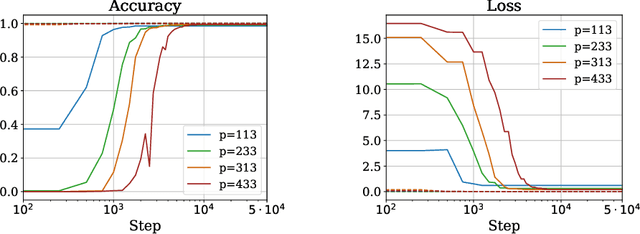
We present a theoretical explanation of the ``grokking'' phenomenon, where a model generalizes long after overfitting,for the originally-studied problem of modular addition. First, we show that early in gradient descent, when the ``kernel regime'' approximately holds, no permutation-equivariant model can achieve small population error on modular addition unless it sees at least a constant fraction of all possible data points. Eventually, however, models escape the kernel regime. We show that two-layer quadratic networks that achieve zero training loss with bounded $\ell_{\infty}$ norm generalize well with substantially fewer training points, and further show such networks exist and can be found by gradient descent with small $\ell_{\infty}$ regularization. We further provide empirical evidence that these networks as well as simple Transformers, leave the kernel regime only after initially overfitting. Taken together, our results strongly support the case for grokking as a consequence of the transition from kernel-like behavior to limiting behavior of gradient descent on deep networks.

Making Look-Ahead Active Learning Strategies Feasible with Neural Tangent Kernels

We propose a new method for approximating active learning acquisition strategies that are based on retraining with hypothetically-labeled candidate data points. Although this is usually infeasible with deep networks, we use the neural tangent kernel to approximate the result of retraining, and prove that this approximation works asymptotically even in an active learning setup -- approximating "look-ahead" selection criteria with far less computation required. This also enables us to conduct sequential active learning, i.e. updating the model in a streaming regime, without needing to retrain the model with SGD after adding each new data point. Moreover, our querying strategy, which better understands how the model's predictions will change by adding new data points in comparison to the standard ("myopic") criteria, beats other look-ahead strategies by large margins, and achieves equal or better performance compared to state-of-the-art methods on several benchmark datasets in pool-based active learning.

A Fast, Well-Founded Approximation to the Empirical Neural Tangent Kernel

Empirical neural tangent kernels (eNTKs) can provide a good understanding of a given network's representation: they are often far less expensive to compute and applicable more broadly than infinite width NTKs. For networks with O output units (e.g. an O-class classifier), however, the eNTK on N inputs is of size $NO \times NO$, taking $O((NO)^2)$ memory and up to $O((NO)^3)$ computation. Most existing applications have therefore used one of a handful of approximations yielding $N \times N$ kernel matrices, saving orders of magnitude of computation, but with limited to no justification. We prove that one such approximation, which we call "sum of logits", converges to the true eNTK at initialization for any network with a wide final "readout" layer. Our experiments demonstrate the quality of this approximation for various uses across a range of settings.