Learning Deep Kernels for Non-Parametric Independence Testing
Paper and Code
Sep 10, 2024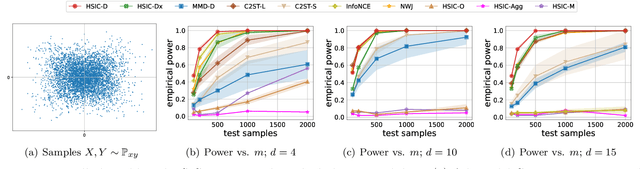

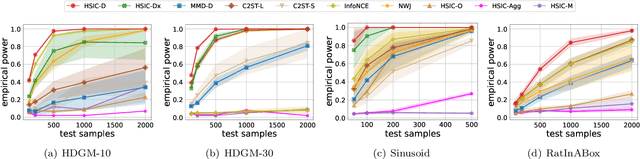
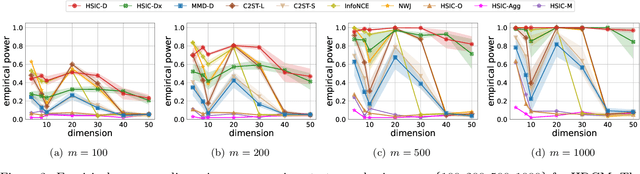
The Hilbert-Schmidt Independence Criterion (HSIC) is a powerful tool for nonparametric detection of dependence between random variables. It crucially depends, however, on the selection of reasonable kernels; commonly-used choices like the Gaussian kernel, or the kernel that yields the distance covariance, are sufficient only for amply sized samples from data distributions with relatively simple forms of dependence. We propose a scheme for selecting the kernels used in an HSIC-based independence test, based on maximizing an estimate of the asymptotic test power. We prove that maximizing this estimate indeed approximately maximizes the true power of the test, and demonstrate that our learned kernels can identify forms of structured dependence between random variables in various experiments.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge