Learning Deep Kernels for Non-Parametric Independence Testing

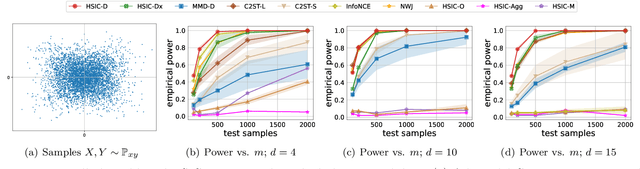
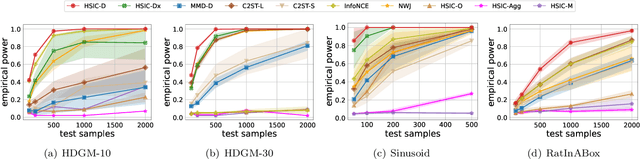
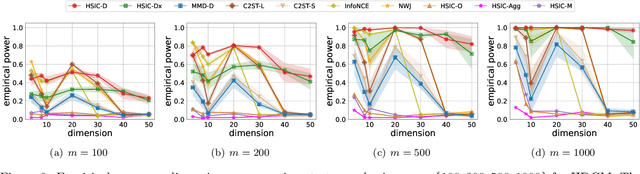
The Hilbert-Schmidt Independence Criterion (HSIC) is a powerful tool for nonparametric detection of dependence between random variables. It crucially depends, however, on the selection of reasonable kernels; commonly-used choices like the Gaussian kernel, or the kernel that yields the distance covariance, are sufficient only for amply sized samples from data distributions with relatively simple forms of dependence. We propose a scheme for selecting the kernels used in an HSIC-based independence test, based on maximizing an estimate of the asymptotic test power. We prove that maximizing this estimate indeed approximately maximizes the true power of the test, and demonstrate that our learned kernels can identify forms of structured dependence between random variables in various experiments.

TrajPAC: Towards Robustness Verification of Pedestrian Trajectory Prediction Models

Robust pedestrian trajectory forecasting is crucial to developing safe autonomous vehicles. Although previous works have studied adversarial robustness in the context of trajectory forecasting, some significant issues remain unaddressed. In this work, we try to tackle these crucial problems. Firstly, the previous definitions of robustness in trajectory prediction are ambiguous. We thus provide formal definitions for two kinds of robustness, namely label robustness and pure robustness. Secondly, as previous works fail to consider robustness about all points in a disturbance interval, we utilise a probably approximately correct (PAC) framework for robustness verification. Additionally, this framework can not only identify potential counterexamples, but also provides interpretable analyses of the original methods. Our approach is applied using a prototype tool named TrajPAC. With TrajPAC, we evaluate the robustness of four state-of-the-art trajectory prediction models -- Trajectron++, MemoNet, AgentFormer, and MID -- on trajectories from five scenes of the ETH/UCY dataset and scenes of the Stanford Drone Dataset. Using our framework, we also experimentally study various factors that could influence robustness performance.

Self-Adapting Noise-Contrastive Estimation for Energy-Based Models

Training energy-based models (EBMs) with noise-contrastive estimation (NCE) is theoretically feasible but practically challenging. Effective learning requires the noise distribution to be approximately similar to the target distribution, especially in high-dimensional domains. Previous works have explored modelling the noise distribution as a separate generative model, and then concurrently training this noise model with the EBM. While this method allows for more effective noise-contrastive estimation, it comes at the cost of extra memory and training complexity. Instead, this thesis proposes a self-adapting NCE algorithm which uses static instances of the EBM along its training trajectory as the noise distribution. During training, these static instances progressively converge to the target distribution, thereby circumventing the need to simultaneously train an auxiliary noise model. Moreover, we express this self-adapting NCE algorithm in the framework of Bregman divergences and show that it is a generalization of maximum likelihood learning for EBMs. The performance of our algorithm is evaluated across a range of noise update intervals, and experimental results show that shorter update intervals are conducive to higher synthesis quality.