Short-Context Dominance: How Much Local Context Natural Language Actually Needs?

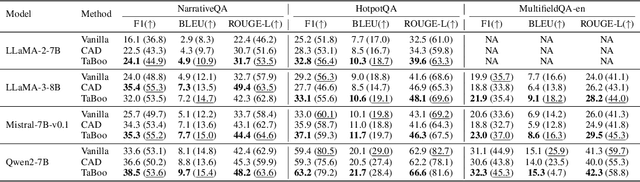
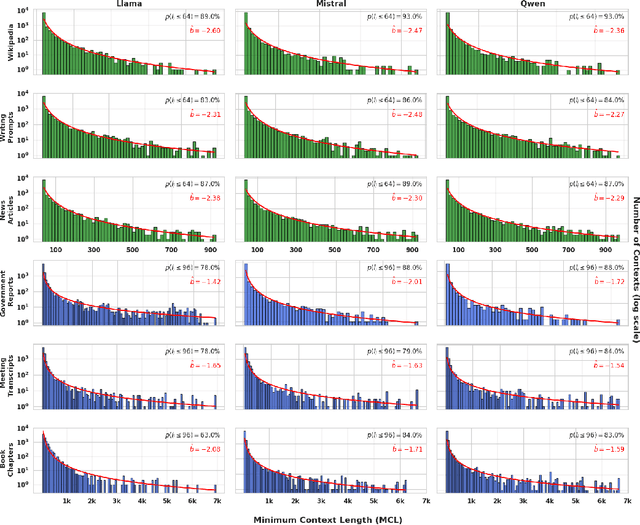
We investigate the short-context dominance hypothesis: that for most sequences, a small local prefix suffices to predict their next tokens. Using large language models as statistical oracles, we measure the minimum context length (MCL) needed to reproduce accurate full-context predictions across datasets with sequences of varying lengths. For sequences with 1-7k tokens from long-context documents, we consistently find that 75-80% require only the last 96 tokens at most. Given the dominance of short-context tokens, we then ask whether it is possible to detect challenging long-context sequences for which a short local prefix does not suffice for prediction. We introduce a practical proxy to MCL, called Distributionally Aware MCL (DaMCL), that does not require knowledge of the actual next-token and is compatible with sampling strategies beyond greedy decoding. Our experiments validate that simple thresholding of the metric defining DaMCL achieves high performance in detecting long vs. short context sequences. Finally, to counter the bias that short-context dominance induces in LLM output distributions, we develop an intuitive decoding algorithm that leverages our detector to identify and boost tokens that are long-range-relevant. Across Q&A tasks and model architectures, we confirm that mitigating the bias improves performance.

Scaling Generative Verifiers For Natural Language Mathematical Proof Verification And Selection

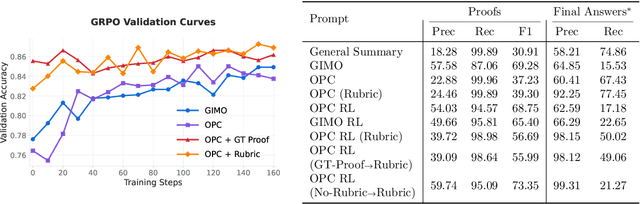
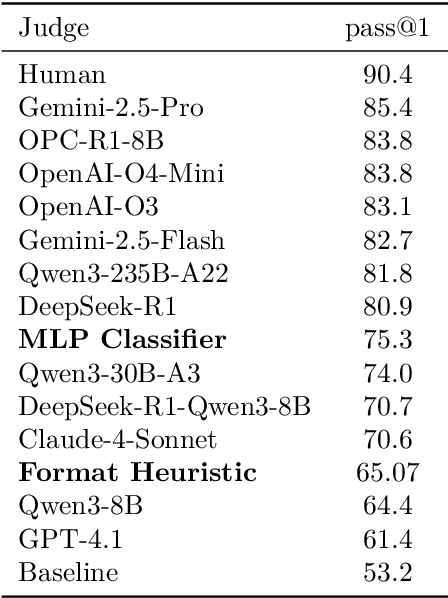
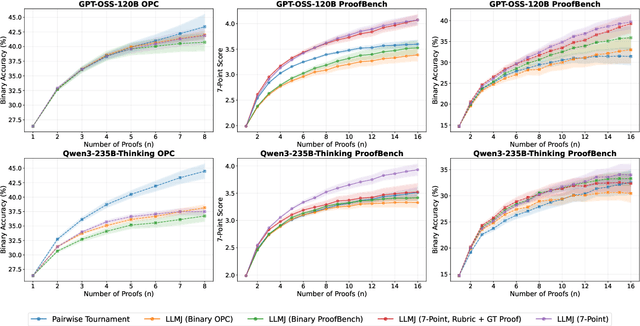
Large language models have achieved remarkable success on final-answer mathematical problems, largely due to the ease of applying reinforcement learning with verifiable rewards. However, the reasoning underlying these solutions is often flawed. Advancing to rigorous proof-based mathematics requires reliable proof verification capabilities. We begin by analyzing multiple evaluation setups and show that focusing on a single benchmark can lead to brittle or misleading conclusions. To address this, we evaluate both proof-based and final-answer reasoning to obtain a more reliable measure of model performance. We then scale two major generative verification methods (GenSelect and LLM-as-a-Judge) to millions of tokens and identify their combination as the most effective framework for solution verification and selection. We further show that the choice of prompt for LLM-as-a-Judge significantly affects the model's performance, but reinforcement learning can reduce this sensitivity. However, despite improving proof-level metrics, reinforcement learning does not enhance final-answer precision, indicating that current models often reward stylistic or procedural correctness rather than mathematical validity. Our results establish practical guidelines for designing and evaluating scalable proof-verification and selection systems.

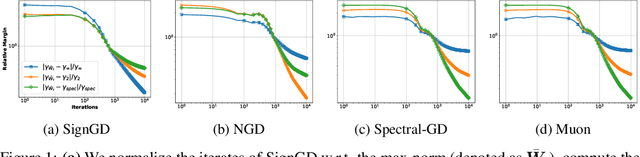
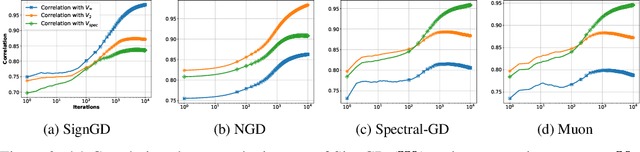
How Muon's Spectral Design Benefits Generalization: A Study on Imbalanced Data

The growing adoption of spectrum-aware matrix-valued optimizers such as Muon and Shampoo in deep learning motivates a systematic study of their generalization properties and, in particular, when they might outperform competitive algorithms. We approach this question by introducing appropriate simplifying abstractions as follows: First, we use imbalanced data as a testbed. Second, we study the canonical form of such optimizers, which is Spectral Gradient Descent (SpecGD) -- each update step is $UV^T$ where $U\Sigma V^T$ is the truncated SVD of the gradient. Third, within this framework we identify a canonical setting for which we precisely quantify when SpecGD outperforms vanilla Euclidean GD. For a Gaussian mixture data model and both linear and bilinear models, we show that unlike GD, which prioritizes learning dominant principal components of the data first, SpecGD learns all principal components of the data at equal rates. We demonstrate how this translates to a growing gap in balanced accuracy favoring SpecGD early in training and further show that the gap remains consistent even when the GD counterpart uses adaptive step-sizes via normalization. By extending the analysis to deep linear models, we show that depth amplifies these effects. We empirically verify our theoretical findings on a variety of imbalanced datasets. Our experiments compare practical variants of spectral methods, like Muon and Shampoo, against their Euclidean counterparts and Adam. The results validate our findings that these spectral optimizers achieve superior generalization by promoting a more balanced learning of the data's underlying components.

Advantage Shaping as Surrogate Reward Maximization: Unifying Pass@K Policy Gradients

This note reconciles two seemingly distinct approaches to policy gradient optimization for the Pass@K objective in reinforcement learning with verifiable rewards: (1) direct REINFORCE-style methods, and (2) advantage-shaping techniques that directly modify GRPO. We show that these are two sides of the same coin. By reverse-engineering existing advantage-shaping algorithms, we reveal that they implicitly optimize surrogate rewards. We specifically interpret practical ``hard-example up-weighting'' modifications to GRPO as reward-level regularization. Conversely, starting from surrogate reward objectives, we provide a simple recipe for deriving both existing and new advantage-shaping methods. This perspective provides a lens for RLVR policy gradient optimization beyond our original motivation of Pass@K.

Efficient Forward-Only Data Valuation for Pretrained LLMs and VLMs

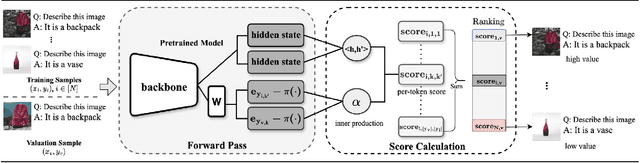
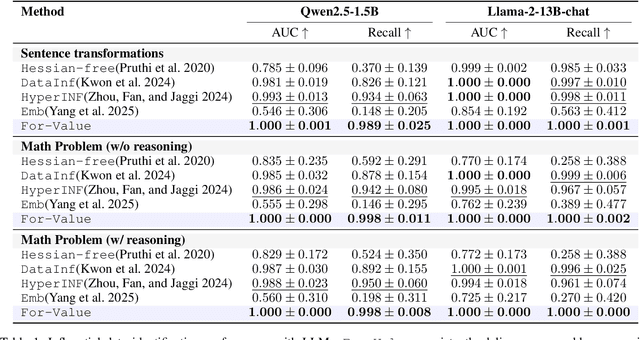
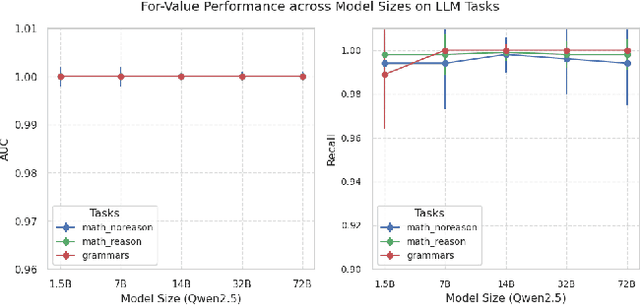
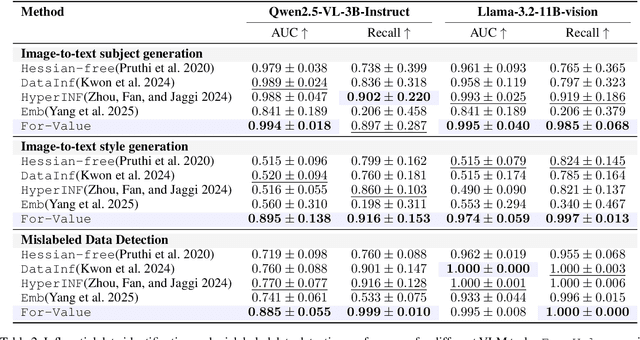
Quantifying the influence of individual training samples is essential for enhancing the transparency and accountability of large language models (LLMs) and vision-language models (VLMs). However, existing data valuation methods often rely on Hessian information or model retraining, making them computationally prohibitive for billion-parameter models. In this work, we introduce For-Value, a forward-only data valuation framework that enables scalable and efficient influence estimation for both LLMs and VLMs. By leveraging the rich representations of modern foundation models, For-Value computes influence scores using a simple closed-form expression based solely on a single forward pass, thereby eliminating the need for costly gradient computations. Our theoretical analysis demonstrates that For-Value accurately estimates per-sample influence by capturing alignment in hidden representations and prediction errors between training and validation samples. Extensive experiments show that For-Value matches or outperforms gradient-based baselines in identifying impactful fine-tuning examples and effectively detecting mislabeled data.

In-Context Occam's Razor: How Transformers Prefer Simpler Hypotheses on the Fly

In-context learning (ICL) enables transformers to adapt to new tasks through contextual examples without parameter updates. While existing research has typically studied ICL in fixed-complexity environments, practical language models encounter tasks spanning diverse complexity levels. This paper investigates how transformers navigate hierarchical task structures where higher-complexity categories can perfectly represent any pattern generated by simpler ones. We design well-controlled testbeds based on Markov chains and linear regression that reveal transformers not only identify the appropriate complexity level for each task but also accurately infer the corresponding parameters--even when the in-context examples are compatible with multiple complexity hypotheses. Notably, when presented with data generated by simpler processes, transformers consistently favor the least complex sufficient explanation. We theoretically explain this behavior through a Bayesian framework, demonstrating that transformers effectively implement an in-context Bayesian Occam's razor by balancing model fit against complexity penalties. We further ablate on the roles of model size, training mixture distribution, inference context length, and architecture. Finally, we validate this Occam's razor-like inductive bias on a pretrained GPT-4 model with Boolean-function tasks as case study, suggesting it may be inherent to transformers trained on diverse task distributions.

On the Effect of Negative Gradient in Group Relative Deep Reinforcement Optimization

Reinforcement learning (RL) has become popular in enhancing the reasoning capabilities of large language models (LLMs), with Group Relative Policy Optimization (GRPO) emerging as a widely used algorithm in recent systems. Despite GRPO's widespread adoption, we identify a previously unrecognized phenomenon we term Lazy Likelihood Displacement (LLD), wherein the likelihood of correct responses marginally increases or even decreases during training. This behavior mirrors a recently discovered misalignment issue in Direct Preference Optimization (DPO), attributed to the influence of negative gradients. We provide a theoretical analysis of GRPO's learning dynamic, identifying the source of LLD as the naive penalization of all tokens in incorrect responses with the same strength. To address this, we develop a method called NTHR, which downweights penalties on tokens contributing to the LLD. Unlike prior DPO-based approaches, NTHR takes advantage of GRPO's group-based structure, using correct responses as anchors to identify influential tokens. Experiments on math reasoning benchmarks demonstrate that NTHR effectively mitigates LLD, yielding consistent performance gains across models ranging from 0.5B to 3B parameters.

On the Geometry of Semantics in Next-token Prediction

Modern language models demonstrate a remarkable ability to capture linguistic meaning despite being trained solely through next-token prediction (NTP). We investigate how this conceptually simple training objective leads models to extract and encode latent semantic and grammatical concepts. Our analysis reveals that NTP optimization implicitly guides models to encode concepts via singular value decomposition (SVD) factors of a centered data-sparsity matrix that captures next-word co-occurrence patterns. While the model never explicitly constructs this matrix, learned word and context embeddings effectively factor it to capture linguistic structure. We find that the most important SVD factors are learned first during training, motivating the use of spectral clustering of embeddings to identify human-interpretable semantics, including both classical k-means and a new orthant-based method directly motivated by our interpretation of concepts. Overall, our work bridges distributional semantics, neural collapse geometry, and neural network training dynamics, providing insights into how NTP's implicit biases shape the emergence of meaning representations in language models.

Implicit Bias of SignGD and Adam on Multiclass Separable Data

In the optimization of overparameterized models, different gradient-based methods can achieve zero training error yet converge to distinctly different solutions inducing different generalization properties. While a decade of research on implicit optimization bias has illuminated this phenomenon in various settings, even the foundational case of linear classification with separable data still has important open questions. We resolve a fundamental gap by characterizing the implicit bias of both Adam and Sign Gradient Descent in multi-class cross-entropy minimization: we prove that their iterates converge to solutions that maximize the margin with respect to the classifier matrix's max-norm and characterize the rate of convergence. We extend our results to general p-norm normalized steepest descent algorithms and to other multi-class losses.

Leveraging Online Olympiad-Level Math Problems for LLMs Training and Contamination-Resistant Evaluation

Advances in Large Language Models (LLMs) have sparked interest in their ability to solve Olympiad-level math problems. However, the training and evaluation of these models are constrained by the limited size and quality of available datasets, as creating large-scale data for such advanced problems requires extensive effort from human experts. In addition, current benchmarks are prone to contamination, leading to unreliable evaluations. In this paper, we present an automated pipeline that leverages the rich resources of the Art of Problem Solving (AoPS) forum, which predominantly features Olympiad-level problems and community-driven solutions. Using open-source LLMs, we develop a method to extract question-answer pairs from the forum, resulting in AoPS-Instruct, a dataset of more than 600,000 high-quality QA pairs. Our experiments demonstrate that fine-tuning LLMs on AoPS-Instruct improves their reasoning abilities across various benchmarks. Moreover, we build an automatic pipeline that introduces LiveAoPSBench, an evolving evaluation set with timestamps, derived from the latest forum data, providing a contamination-resistant benchmark for assessing LLM performance. Notably, we observe a significant decline in LLM performance over time, suggesting their success on older examples may stem from pre-training exposure rather than true reasoning ability. Our work presents a scalable approach to creating and maintaining large-scale, high-quality datasets for advanced math reasoning, offering valuable insights into the capabilities and limitations of LLMs in this domain. Our benchmark and code is available at https://github.com/DSL-Lab/aops