Upper and lower memory capacity bounds of transformers for next-token prediction

Given a sequence of tokens, such as words, the task of next-token prediction is to predict the next-token conditional probability distribution. Decoder-only transformers have become effective models for this task, but their properties are still not fully understood. In particular, the largest number of distinct context sequences that a decoder-only transformer can interpolate next-token distributions for has not been established. To fill this gap, we prove upper and lower bounds on this number, which are equal up to a multiplicative constant. We prove these bounds in the general setting where next-token distributions can be arbitrary as well as the empirical setting where they are calculated from a finite number of document sequences. Our lower bounds are for one-layer transformers and our proofs highlight an important injectivity property satisfied by self-attention. Furthermore, we provide numerical evidence that the minimal number of parameters for memorization is sufficient for being able to train the model to the entropy lower bound.

Memory capacity of three-layer neural networks with non-polynomial activations

The minimal number of neurons required for a feedforward neural network to interpolate $n$ generic input-output pairs from $\mathbb{R}^d\times \mathbb{R}$ is $\Theta(\sqrt{n})$. While previous results have shown that $\Theta(\sqrt{n})$ neurons are sufficient, they have been limited to logistic, Heaviside, and rectified linear unit (ReLU) as the activation function. Using a different approach, we prove that $\Theta(\sqrt{n})$ neurons are sufficient as long as the activation function is real analytic at a point and not a polynomial there. Thus, the only practical activation functions that our result does not apply to are piecewise polynomials. Importantly, this means that activation functions can be freely chosen in a problem-dependent manner without loss of interpolation power.

Memory capacity of two layer neural networks with smooth activations

Determining the memory capacity of two-layer neural networks with m hidden neurons and input dimension d (i.e., md+m total trainable parameters), which refers to the largest size of general data the network can memorize, is a fundamental machine-learning question. For non-polynomial real analytic activation functions, such as sigmoids and smoothed rectified linear units (smoothed ReLUs), we establish a lower bound of md/2 and optimality up to a factor of approximately 2. Analogous prior results were limited to Heaviside and ReLU activations, with results for smooth activations suffering from logarithmic factors and requiring random data. To analyze the memory capacity, we examine the rank of the network's Jacobian by computing the rank of matrices involving both Hadamard powers and the Khati-Rao product. Our computation extends classical linear algebraic facts about the rank of Hadamard powers. Overall, our approach differs from previous works on memory capacity and holds promise for extending to deeper models and other architectures.

Optimization and Learning with Information Streams: Time-varying Algorithms and Applications

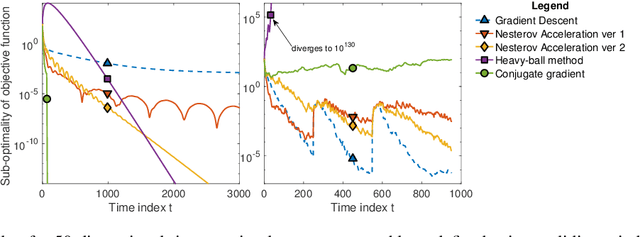
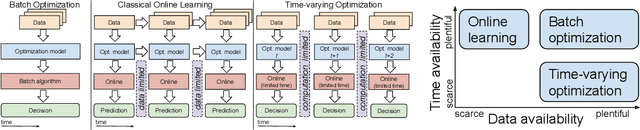
There is a growing cross-disciplinary effort in the broad domain of optimization and learning with streams of data, applied to settings where traditional batch optimization techniques cannot produce solutions at time scales that match the inter-arrival times of the data points due to computational and/or communication bottlenecks. Special types of online algorithms can handle this situation, and this article focuses on such time-varying optimization algorithms, with emphasis on Machine Leaning and Signal Processing, as well as data-driven control. Approaches for the design of time-varying first-order methods are discussed, with emphasis on algorithms that can handle errors in the gradient, as may arise when the gradient is estimated. Insights on performance metrics and accompanying claims are provided, along with evidence of cases where algorithms that are provably convergent in batch optimization perform poorly in an online regime. The role of distributed computation is discussed. Illustrative numerical examples for a number of applications of broad interest are provided to convey key ideas.