WENDy for Nonlinear-in-Parameter ODEs

The Weak-form Estimation of Non-linear Dynamics (WENDy) algorithm is extended to accommodate systems of ordinary differential equations that are nonlinear-in-parameters (NiP). The extension rests on derived analytic expressions for a likelihood function, its gradient and its Hessian matrix. WENDy makes use of these to approximate a maximum likelihood estimator based on optimization routines suited for non-convex optimization problems. The resulting parameter estimation algorithm has better accuracy, a substantially larger domain of convergence, and is often orders of magnitude faster than the conventional output error least squares method (based on forward solvers). The WENDy.jl algorithm is efficiently implemented in Julia. We demonstrate the algorithm's ability to accommodate the weak form optimization for both additive normal and multiplicative log-normal noise, and present results on a suite of benchmark systems of ordinary differential equations. In order to demonstrate the practical benefits of our approach, we present extensive comparisons between our method and output error methods in terms of accuracy, precision, bias, and coverage.

Exploring Exploration in Bayesian Optimization

A well-balanced exploration-exploitation trade-off is crucial for successful acquisition functions in Bayesian optimization. However, there is a lack of quantitative measures for exploration, making it difficult to analyze and compare different acquisition functions. This work introduces two novel approaches - observation traveling salesman distance and observation entropy - to quantify the exploration characteristics of acquisition functions based on their selected observations. Using these measures, we examine the explorative nature of several well-known acquisition functions across a diverse set of black-box problems, uncover links between exploration and empirical performance, and reveal new relationships among existing acquisition functions. Beyond enabling a deeper understanding of acquisition functions, these measures also provide a foundation for guiding their design in a more principled and systematic manner.

A Unified Framework for Entropy Search and Expected Improvement in Bayesian Optimization

Bayesian optimization is a widely used method for optimizing expensive black-box functions, with Expected Improvement being one of the most commonly used acquisition functions. In contrast, information-theoretic acquisition functions aim to reduce uncertainty about the function's optimum and are often considered fundamentally distinct from EI. In this work, we challenge this prevailing perspective by introducing a unified theoretical framework, Variational Entropy Search, which reveals that EI and information-theoretic acquisition functions are more closely related than previously recognized. We demonstrate that EI can be interpreted as a variational inference approximation of the popular information-theoretic acquisition function, named Max-value Entropy Search. Building on this insight, we propose VES-Gamma, a novel acquisition function that balances the strengths of EI and MES. Extensive empirical evaluations across both low- and high-dimensional synthetic and real-world benchmarks demonstrate that VES-Gamma is competitive with state-of-the-art acquisition functions and in many cases outperforms EI and MES.

Evaluation of data driven low-rank matrix factorization for accelerated solutions of the Vlasov equation

Low-rank methods have shown success in accelerating simulations of a collisionless plasma described by the Vlasov equation, but still rely on computationally costly linear algebra every time step. We propose a data-driven factorization method using artificial neural networks, specifically with convolutional layer architecture, that trains on existing simulation data. At inference time, the model outputs a low-rank decomposition of the distribution field of the charged particles, and we demonstrate that this step is faster than the standard linear algebra technique. Numerical experiments show that the method effectively interpolates time-series data, generalizing to unseen test data in a manner beyond just memorizing training data; patterns in factorization also inherently followed the same numerical trend as those within algebraic methods (e.g., truncated singular-value decomposition). However, when training on the first 70% of a time-series data and testing on the remaining 30%, the method fails to meaningfully extrapolate. Despite this limiting result, the technique may have benefits for simulations in a statistical steady-state or otherwise showing temporal stability.

Optimization of Array Encoding for Ultrasound Imaging

Objective: The transmit encoding model for synthetic aperture imaging is a robust and flexible framework for understanding the effect of acoustic transmission on ultrasound image reconstruction. Our objective is to use machine learning (ML) to construct scanning sequences, parameterized by time delays and apodization weights, that produce high quality B-mode images. Approach: We use an ML model in PyTorch and simulated RF data from Field II to probe the space of possible encoding sequences for those that minimize a loss function that describes image quality. This approach is made computationally feasible by a novel formulation of the derivative for delay-and-sum beamforming. We demonstrate these results experimentally on wire targets and a tissue-mimicking phantom. Main Results: When trained according to a given set of imaging parameters (imaging domain, hardware restrictions), our ML imaging model produces optimized encoding sequences that improve a number of standard quality metrics including resolution, field of view, and contrast, over conventional sequences. Significance: This work demonstrates that the set of encoding schemes that are commonly used represent only a narrow subset of those available. Additionally, it demonstrates the value for ML tasks in synthetic transmit aperture imaging to consider the beamformer within the model, instead of as purely post-processing.

Variational Entropy Search for Adjusting Expected Improvement

Bayesian optimization is a widely used technique for optimizing black-box functions, with Expected Improvement (EI) being the most commonly utilized acquisition function in this domain. While EI is often viewed as distinct from other information-theoretic acquisition functions, such as entropy search (ES) and max-value entropy search (MES), our work reveals that EI can be considered a special case of MES when approached through variational inference (VI). In this context, we have developed the Variational Entropy Search (VES) methodology and the VES-Gamma algorithm, which adapts EI by incorporating principles from information-theoretic concepts. The efficacy of VES-Gamma is demonstrated across a variety of test functions and read datasets, highlighting its theoretical and practical utilities in Bayesian optimization scenarios.

In Situ Framework for Coupling Simulation and Machine Learning with Application to CFD

Recent years have seen many successful applications of machine learning (ML) to facilitate fluid dynamic computations. As simulations grow, generating new training datasets for traditional offline learning creates I/O and storage bottlenecks. Additionally, performing inference at runtime requires non-trivial coupling of ML framework libraries with simulation codes. This work offers a solution to both limitations by simplifying this coupling and enabling in situ training and inference workflows on heterogeneous clusters. Leveraging SmartSim, the presented framework deploys a database to store data and ML models in memory, thus circumventing the file system. On the Polaris supercomputer, we demonstrate perfect scaling efficiency to the full machine size of the data transfer and inference costs thanks to a novel co-located deployment of the database. Moreover, we train an autoencoder in situ from a turbulent flow simulation, showing that the framework overhead is negligible relative to a solver time step and training epoch.

Bi-fidelity Variational Auto-encoder for Uncertainty Quantification

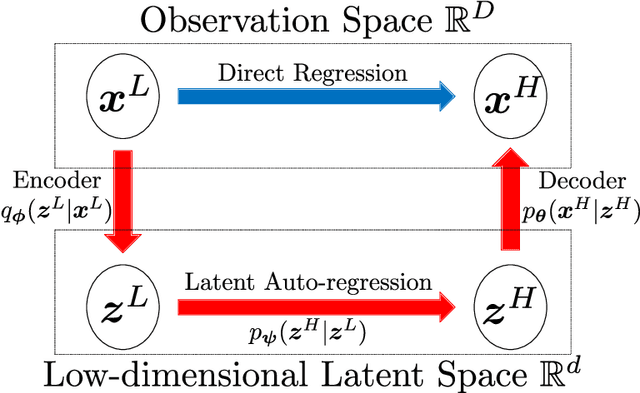
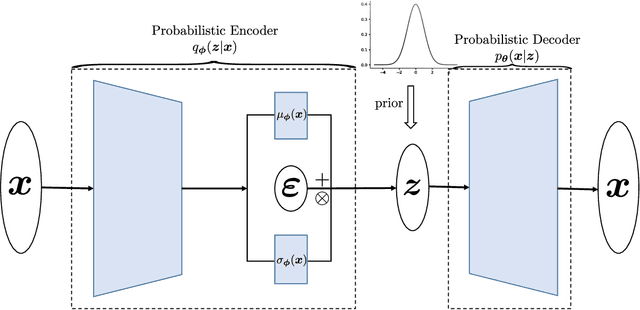
Quantifying the uncertainty of quantities of interest (QoIs) from physical systems is a primary objective in model validation. However, achieving this goal entails balancing the need for computational efficiency with the requirement for numerical accuracy. To address this trade-off, we propose a novel bi-fidelity formulation of variational auto-encoders (BF-VAE) designed to estimate the uncertainty associated with a QoI from low-fidelity (LF) and high-fidelity (HF) samples of the QoI. This model allows for the approximation of the statistics of the HF QoI by leveraging information derived from its LF counterpart. Specifically, we design a bi-fidelity auto-regressive model in the latent space that is integrated within the VAE's probabilistic encoder-decoder structure. An effective algorithm is proposed to maximize the variational lower bound of the HF log-likelihood in the presence of limited HF data, resulting in the synthesis of HF realizations with a reduced computational cost. Additionally, we introduce the concept of the bi-fidelity information bottleneck (BF-IB) to provide an information-theoretic interpretation of the proposed BF-VAE model. Our numerical results demonstrate that BF-VAE leads to considerably improved accuracy, as compared to a VAE trained using only HF data when limited HF data is available.

The Dependence of Parallel Imaging with Linear Predictability on the Undersampling Direction

Parallel imaging with linear predictability takes advantage of information present in multiple receive coils to accurately reconstruct the image with fewer samples. Commonly used algorithms based on linear predictability include GRAPPA and SPIRiT. We present a sufficient condition for reconstruction based on the direction of undersampling and the arrangement of the sensing coils. This condition is justified theoretically and examples are shown using real data. We also propose a metric based on the fully-sampled auto-calibration region which can show which direction(s) of undersampling will allow for a good quality image reconstruction.

QCNN: Quadrature Convolutional Neural Network with Application to Unstructured Data Compression

We present a new convolution layer for deep learning architectures which we call QuadConv -- an approximation to continuous convolution via quadrature. Our operator is developed explicitly for use on unstructured data, and accomplishes this by learning a continuous kernel that can be sampled at arbitrary locations. In the setting of neural compression, we show that a QuadConv-based autoencoder, resulting in a Quadrature Convolutional Neural Network (QCNN), can match the performance of standard discrete convolutions on structured uniform data, as in CNNs, and maintain this accuracy on unstructured data.