Aligning to What? Limits to RLHF Based Alignment

Reinforcement Learning from Human Feedback (RLHF) is increasingly used to align large language models (LLMs) with human preferences. However, the effectiveness of RLHF in addressing underlying biases remains unclear. This study investigates the relationship between RLHF and both covert and overt biases in LLMs, particularly focusing on biases against African Americans. We applied various RLHF techniques (DPO, ORPO, and RLOO) to Llama 3 8B and evaluated the covert and overt biases of the resulting models using matched-guise probing and explicit bias testing. We performed additional tests with DPO on different base models and datasets; among several implications, we found that SFT before RLHF calcifies model biases. Additionally, we extend the tools for measuring biases to multi-modal models. Through our experiments we collect evidence that indicates that current alignment techniques are inadequate for nebulous tasks such as mitigating covert biases, highlighting the need for capable datasets, data curating techniques, or alignment tools.

Fine Tuning without Catastrophic Forgetting via Selective Low Rank Adaptation

Adapting deep learning models to new domains often requires computationally intensive retraining and risks catastrophic forgetting. While fine-tuning enables domain-specific adaptation, it can reduce robustness to distribution shifts, impacting out-of-distribution (OOD) performance. Pre-trained zero-shot models like CLIP offer strong generalization but may suffer degraded robustness after fine-tuning. Building on Task Adaptive Parameter Sharing (TAPS), we propose a simple yet effective extension as a parameter-efficient fine-tuning (PEFT) method, using an indicator function to selectively activate Low-Rank Adaptation (LoRA) blocks. Our approach minimizes knowledge loss, retains its generalization strengths under domain shifts, and significantly reduces computational costs compared to traditional fine-tuning. We demonstrate that effective fine-tuning can be achieved with as few as 5\% of active blocks, substantially improving efficiency. Evaluations on pre-trained models such as CLIP and DINO-ViT demonstrate our method's broad applicability and effectiveness in maintaining performance and knowledge retention.

Where Did Your Model Learn That? Label-free Influence for Self-supervised Learning

Self-supervised learning (SSL) has revolutionized learning from large-scale unlabeled datasets, yet the intrinsic relationship between pretraining data and the learned representations remains poorly understood. Traditional supervised learning benefits from gradient-based data attribution tools like influence functions that measure the contribution of an individual data point to model predictions. However, existing definitions of influence rely on labels, making them unsuitable for SSL settings. We address this gap by introducing Influence-SSL, a novel and label-free approach for defining influence functions tailored to SSL. Our method harnesses the stability of learned representations against data augmentations to identify training examples that help explain model predictions. We provide both theoretical foundations and empirical evidence to show the utility of Influence-SSL in analyzing pre-trained SSL models. Our analysis reveals notable differences in how SSL models respond to influential data compared to supervised models. Finally, we validate the effectiveness of Influence-SSL through applications in duplicate detection, outlier identification and fairness analysis. Code is available at: \url{https://github.com/cryptonymous9/Influence-SSL}.

Physics-Informed Neural Networks and Extensions

In this paper, we review the new method Physics-Informed Neural Networks (PINNs) that has become the main pillar in scientific machine learning, we present recent practical extensions, and provide a specific example in data-driven discovery of governing differential equations.

Physics-Informed Machine Learning for Smart Additive Manufacturing

Compared to physics-based computational manufacturing, data-driven models such as machine learning (ML) are alternative approaches to achieve smart manufacturing. However, the data-driven ML's "black box" nature has presented a challenge to interpreting its outcomes. On the other hand, governing physical laws are not effectively utilized to develop data-efficient ML algorithms. To leverage the advantages of ML and physical laws of advanced manufacturing, this paper focuses on the development of a physics-informed machine learning (PIML) model by integrating neural networks and physical laws to improve model accuracy, transparency, and generalization with case studies in laser metal deposition (LMD).

Mixing Natural and Synthetic Images for Robust Self-Supervised Representations

This paper introduces DiffMix, a new self-supervised learning (SSL) pre-training framework that combines real and synthetic images. Unlike traditional SSL methods that predominantly use real images, DiffMix uses a variant of Stable Diffusion to replace an augmented instance of a real image, facilitating the learning of cross real-synthetic image representations. The key insight is that while SSL methods trained solely on synthetic images underperform compared to those trained on real images, a blended training approach using both real and synthetic images leads to more robust and adaptable representations. Experiments demonstrate that DiffMix enhances the SSL methods SimCLR, BarlowTwins, and DINO, across various robustness datasets and domain transfer tasks. DiffMix boosts SimCLR's accuracy on ImageNet-1K by 4.56\%. These results challenge the notion that high-quality real images are crucial for SSL pre-training by showing that lower quality synthetic images can also produce strong representations. DiffMix also reduces the need for image augmentations in SSL, offering new optimization strategies.

Parameter Efficient Fine-tuning of Self-supervised ViTs without Catastrophic Forgetting

Artificial neural networks often suffer from catastrophic forgetting, where learning new concepts leads to a complete loss of previously acquired knowledge. We observe that this issue is particularly magnified in vision transformers (ViTs), where post-pre-training and fine-tuning on new tasks can significantly degrade the model's original general abilities. For instance, a DINO ViT-Base/16 pre-trained on ImageNet-1k loses over 70% accuracy on ImageNet-1k after just 10 iterations of fine-tuning on CIFAR-100. Overcoming this stability-plasticity dilemma is crucial for enabling ViTs to continuously learn and adapt to new domains while preserving their initial knowledge. In this work, we study two new parameter-efficient fine-tuning strategies: (1)~Block Expansion, and (2) Low-rank adaptation (LoRA). Our experiments reveal that using either Block Expansion or LoRA on self-supervised pre-trained ViTs surpass fully fine-tuned ViTs in new domains while offering significantly greater parameter efficiency. Notably, we find that Block Expansion experiences only a minimal performance drop in the pre-training domain, thereby effectively mitigating catastrophic forgetting in pre-trained ViTs.

A Survey on Physics Informed Reinforcement Learning: Review and Open Problems

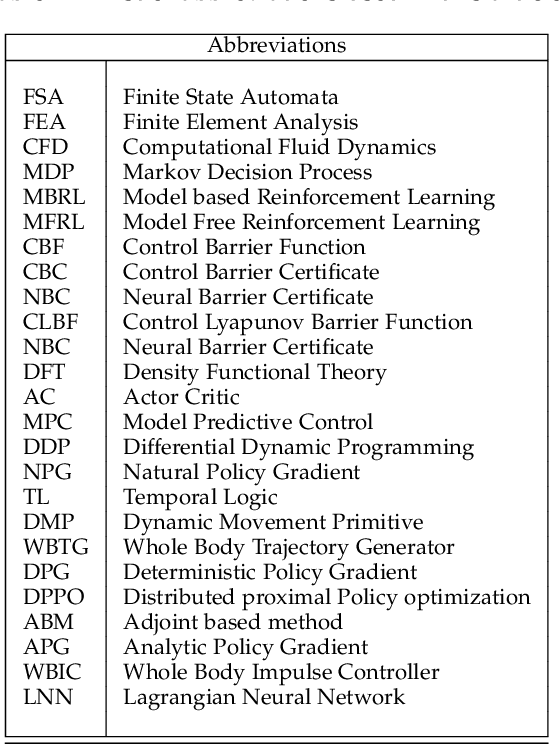
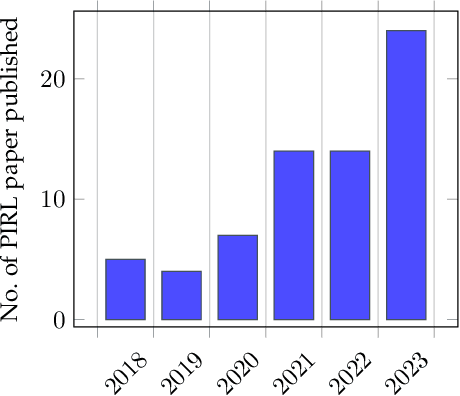
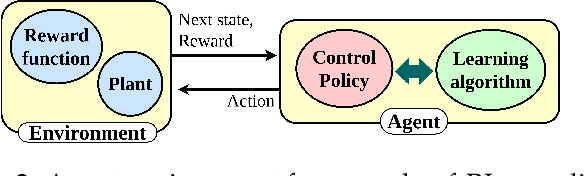
The inclusion of physical information in machine learning frameworks has revolutionized many application areas. This involves enhancing the learning process by incorporating physical constraints and adhering to physical laws. In this work we explore their utility for reinforcement learning applications. We present a thorough review of the literature on incorporating physics information, as known as physics priors, in reinforcement learning approaches, commonly referred to as physics-informed reinforcement learning (PIRL). We introduce a novel taxonomy with the reinforcement learning pipeline as the backbone to classify existing works, compare and contrast them, and derive crucial insights. Existing works are analyzed with regard to the representation/ form of the governing physics modeled for integration, their specific contribution to the typical reinforcement learning architecture, and their connection to the underlying reinforcement learning pipeline stages. We also identify core learning architectures and physics incorporation biases (i.e., observational, inductive and learning) of existing PIRL approaches and use them to further categorize the works for better understanding and adaptation. By providing a comprehensive perspective on the implementation of the physics-informed capability, the taxonomy presents a cohesive approach to PIRL. It identifies the areas where this approach has been applied, as well as the gaps and opportunities that exist. Additionally, the taxonomy sheds light on unresolved issues and challenges, which can guide future research. This nascent field holds great potential for enhancing reinforcement learning algorithms by increasing their physical plausibility, precision, data efficiency, and applicability in real-world scenarios.

Real Estate Property Valuation using Self-Supervised Vision Transformers

The use of Artificial Intelligence (AI) in the real estate market has been growing in recent years. In this paper, we propose a new method for property valuation that utilizes self-supervised vision transformers, a recent breakthrough in computer vision and deep learning. Our proposed algorithm uses a combination of machine learning, computer vision and hedonic pricing models trained on real estate data to estimate the value of a given property. We collected and pre-processed a data set of real estate properties in the city of Boulder, Colorado and used it to train, validate and test our algorithm. Our data set consisted of qualitative images (including house interiors, exteriors, and street views) as well as quantitative features such as the number of bedrooms, bathrooms, square footage, lot square footage, property age, crime rates, and proximity to amenities. We evaluated the performance of our model using metrics such as Root Mean Squared Error (RMSE). Our findings indicate that these techniques are able to accurately predict the value of properties, with a low RMSE. The proposed algorithm outperforms traditional appraisal methods that do not leverage property images and has the potential to be used in real-world applications.

Temporal Consistency Loss for Physics-Informed Neural Networks

Physics-informed neural networks (PINNs) have been widely used to solve partial differential equations in a forward and inverse manner using deep neural networks. However, training these networks can be challenging for multiscale problems. While statistical methods can be employed to scale the regression loss on data, it is generally challenging to scale the loss terms for equations. This paper proposes a method for scaling the mean squared loss terms in the objective function used to train PINNs. Instead of using automatic differentiation to calculate the temporal derivative, we use backward Euler discretization. This provides us with a scaling term for the equations. In this work, we consider the two and three-dimensional Navier-Stokes equations and determine the kinematic viscosity using the spatio-temporal data on the velocity and pressure fields. We first consider numerical datasets to test our method. We test the sensitivity of our method to the time step size, the number of timesteps, noise in the data, and spatial resolution. Finally, we use the velocity field obtained using Particle Image Velocimetry (PIV) experiments to generate a reference pressure field. We then test our framework using the velocity and reference pressure field.