Nuojin Cheng
Stochastic Subspace Descent Accelerated via Bi-fidelity Line Search
Apr 30, 2025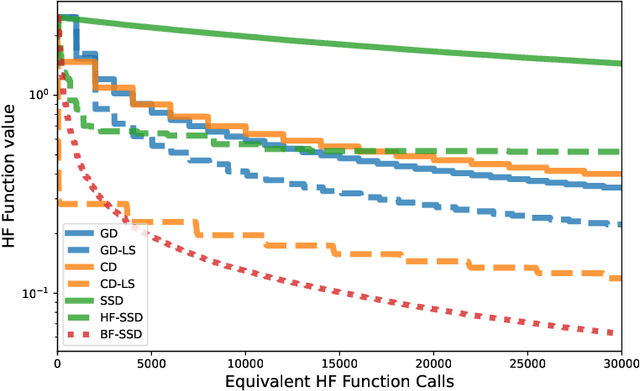
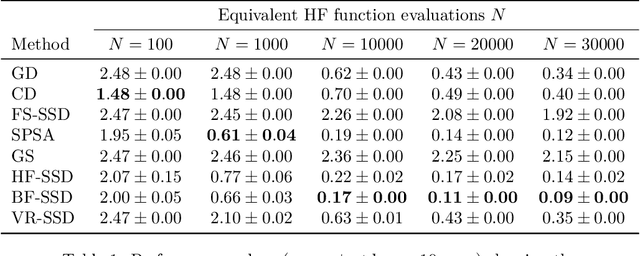
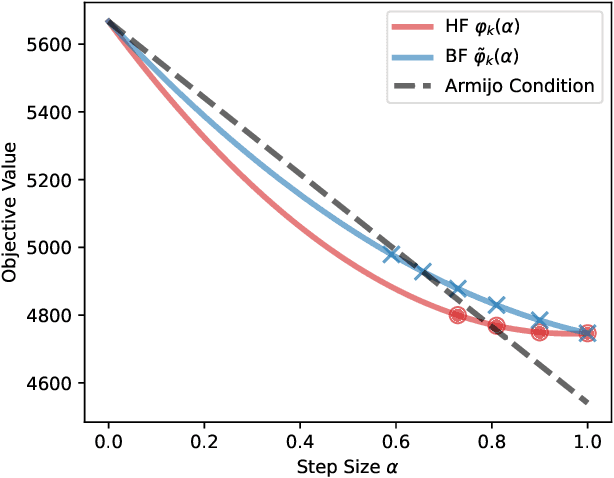
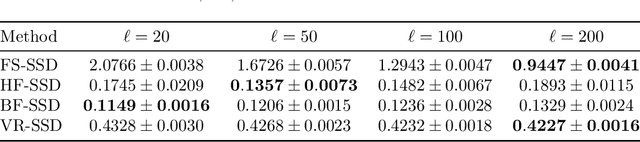
Abstract:Efficient optimization remains a fundamental challenge across numerous scientific and engineering domains, especially when objective function and gradient evaluations are computationally expensive. While zeroth-order optimization methods offer effective approaches when gradients are inaccessible, their practical performance can be limited by the high cost associated with function queries. This work introduces the bi-fidelity stochastic subspace descent (BF-SSD) algorithm, a novel zeroth-order optimization method designed to reduce this computational burden. BF-SSD leverages a bi-fidelity framework, constructing a surrogate model from a combination of computationally inexpensive low-fidelity (LF) and accurate high-fidelity (HF) function evaluations. This surrogate model facilitates an efficient backtracking line search for step size selection, for which we provide theoretical convergence guarantees under standard assumptions. We perform a comprehensive empirical evaluation of BF-SSD across four distinct problems: a synthetic optimization benchmark, dual-form kernel ridge regression, black-box adversarial attacks on machine learning models, and transformer-based black-box language model fine-tuning. Numerical results demonstrate that BF-SSD consistently achieves superior optimization performance while requiring significantly fewer HF function evaluations compared to relevant baseline methods. This study highlights the efficacy of integrating bi-fidelity strategies within zeroth-order optimization, positioning BF-SSD as a promising and computationally efficient approach for tackling large-scale, high-dimensional problems encountered in various real-world applications.
Exploring Exploration in Bayesian Optimization
Feb 12, 2025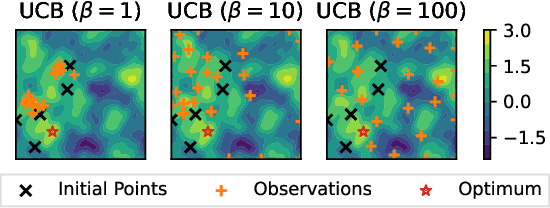
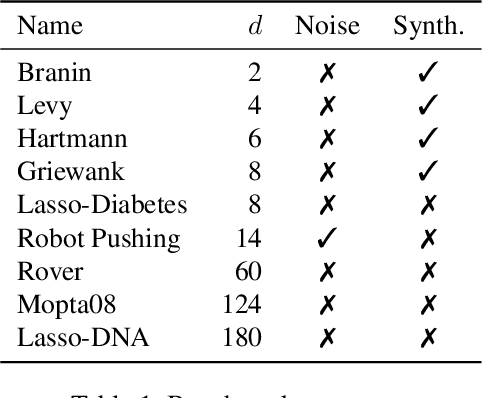
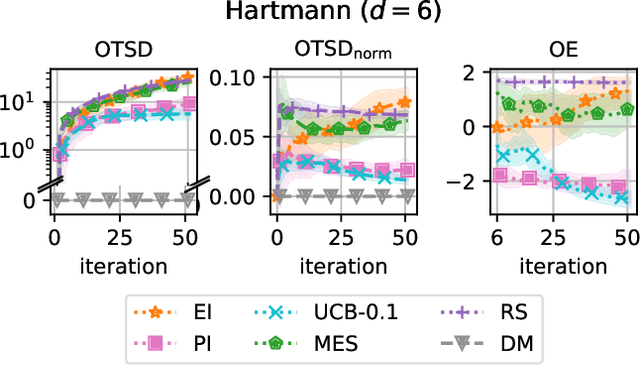
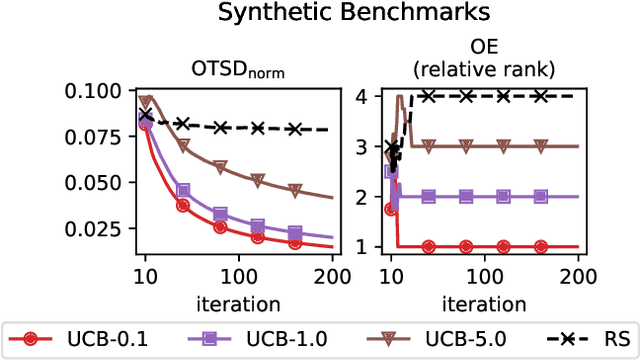
Abstract:A well-balanced exploration-exploitation trade-off is crucial for successful acquisition functions in Bayesian optimization. However, there is a lack of quantitative measures for exploration, making it difficult to analyze and compare different acquisition functions. This work introduces two novel approaches - observation traveling salesman distance and observation entropy - to quantify the exploration characteristics of acquisition functions based on their selected observations. Using these measures, we examine the explorative nature of several well-known acquisition functions across a diverse set of black-box problems, uncover links between exploration and empirical performance, and reveal new relationships among existing acquisition functions. Beyond enabling a deeper understanding of acquisition functions, these measures also provide a foundation for guiding their design in a more principled and systematic manner.
A Unified Framework for Entropy Search and Expected Improvement in Bayesian Optimization
Jan 30, 2025Abstract:Bayesian optimization is a widely used method for optimizing expensive black-box functions, with Expected Improvement being one of the most commonly used acquisition functions. In contrast, information-theoretic acquisition functions aim to reduce uncertainty about the function's optimum and are often considered fundamentally distinct from EI. In this work, we challenge this prevailing perspective by introducing a unified theoretical framework, Variational Entropy Search, which reveals that EI and information-theoretic acquisition functions are more closely related than previously recognized. We demonstrate that EI can be interpreted as a variational inference approximation of the popular information-theoretic acquisition function, named Max-value Entropy Search. Building on this insight, we propose VES-Gamma, a novel acquisition function that balances the strengths of EI and MES. Extensive empirical evaluations across both low- and high-dimensional synthetic and real-world benchmarks demonstrate that VES-Gamma is competitive with state-of-the-art acquisition functions and in many cases outperforms EI and MES.
Variational Entropy Search for Adjusting Expected Improvement
Feb 17, 2024



Abstract:Bayesian optimization is a widely used technique for optimizing black-box functions, with Expected Improvement (EI) being the most commonly utilized acquisition function in this domain. While EI is often viewed as distinct from other information-theoretic acquisition functions, such as entropy search (ES) and max-value entropy search (MES), our work reveals that EI can be considered a special case of MES when approached through variational inference (VI). In this context, we have developed the Variational Entropy Search (VES) methodology and the VES-Gamma algorithm, which adapts EI by incorporating principles from information-theoretic concepts. The efficacy of VES-Gamma is demonstrated across a variety of test functions and read datasets, highlighting its theoretical and practical utilities in Bayesian optimization scenarios.
Bi-fidelity Variational Auto-encoder for Uncertainty Quantification
May 25, 2023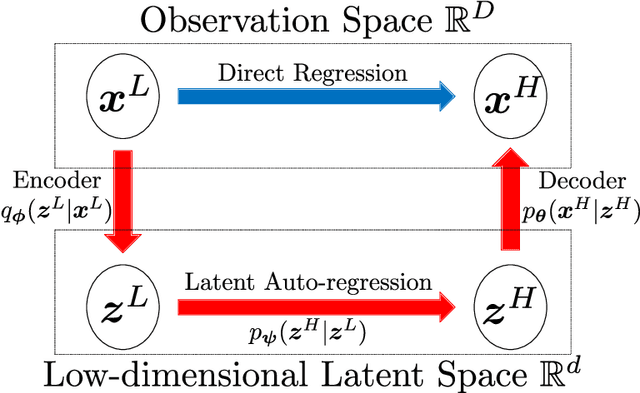

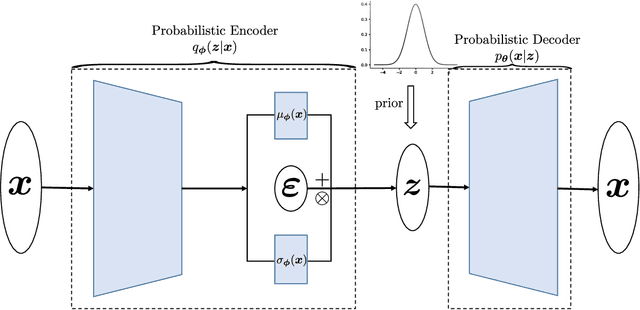

Abstract:Quantifying the uncertainty of quantities of interest (QoIs) from physical systems is a primary objective in model validation. However, achieving this goal entails balancing the need for computational efficiency with the requirement for numerical accuracy. To address this trade-off, we propose a novel bi-fidelity formulation of variational auto-encoders (BF-VAE) designed to estimate the uncertainty associated with a QoI from low-fidelity (LF) and high-fidelity (HF) samples of the QoI. This model allows for the approximation of the statistics of the HF QoI by leveraging information derived from its LF counterpart. Specifically, we design a bi-fidelity auto-regressive model in the latent space that is integrated within the VAE's probabilistic encoder-decoder structure. An effective algorithm is proposed to maximize the variational lower bound of the HF log-likelihood in the presence of limited HF data, resulting in the synthesis of HF realizations with a reduced computational cost. Additionally, we introduce the concept of the bi-fidelity information bottleneck (BF-IB) to provide an information-theoretic interpretation of the proposed BF-VAE model. Our numerical results demonstrate that BF-VAE leads to considerably improved accuracy, as compared to a VAE trained using only HF data when limited HF data is available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge