Boundary condition enforcement with PINNs: a comparative study and verification on 3D geometries

Since their advent nearly a decade ago, physics-informed neural networks (PINNs) have been studied extensively as a novel technique for solving forward and inverse problems in physics and engineering. The neural network discretization of the solution field is naturally adaptive and avoids meshing the computational domain, which can both improve the accuracy of the numerical solution and streamline implementation. However, there have been limited studies of PINNs on complex three-dimensional geometries, as the lack of mesh and the reliance on the strong form of the partial differential equation (PDE) make boundary condition (BC) enforcement challenging. Techniques to enforce BCs with PINNs have proliferated in the literature, but a comprehensive side-by-side comparison of these techniques and a study of their efficacy on geometrically complex three-dimensional test problems are lacking. In this work, we i) systematically compare BC enforcement techniques for PINNs, ii) propose a general solution framework for arbitrary three-dimensional geometries, and iii) verify the methodology on three-dimensional, linear and nonlinear test problems with combinations of Dirichlet, Neumann, and Robin boundaries. Our approach is agnostic to the underlying PDE, the geometry of the computational domain, and the nature of the BCs, while requiring minimal hyperparameter tuning. This work represents a step in the direction of establishing PINNs as a mature numerical method, capable of competing head-to-head with incumbents such as the finite element method.

Solving engineering eigenvalue problems with neural networks using the Rayleigh quotient

From characterizing the speed of a thermal system's response to computing natural modes of vibration, eigenvalue analysis is ubiquitous in engineering. In spite of this, eigenvalue problems have received relatively little treatment compared to standard forward and inverse problems in the physics-informed machine learning literature. In particular, neural network discretizations of solutions to eigenvalue problems have seen only a handful of studies. Owing to their nonlinearity, neural network discretizations prevent the conversion of the continuous eigenvalue differential equation into a standard discrete eigenvalue problem. In this setting, eigenvalue analysis requires more specialized techniques. Using a neural network discretization of the eigenfunction, we show that a variational form of the eigenvalue problem called the "Rayleigh quotient" in tandem with a Gram-Schmidt orthogonalization procedure is a particularly simple and robust approach to find the eigenvalues and their corresponding eigenfunctions. This method is shown to be useful for finding sets of harmonic functions on irregular domains, parametric and nonlinear eigenproblems, and high-dimensional eigenanalysis. We also discuss the utility of harmonic functions as a spectral basis for approximating solutions to partial differential equations. Through various examples from engineering mechanics, the combination of the Rayleigh quotient objective, Gram-Schmidt procedure, and the neural network discretization of the eigenfunction is shown to offer unique advantages for handling continuous eigenvalue problems.

Physics-informed solution reconstruction in elasticity and heat transfer using the explicit constraint force method

One use case of ``physics-informed neural networks'' (PINNs) is solution reconstruction, which aims to estimate the full-field state of a physical system from sparse measurements. Parameterized governing equations of the system are used in tandem with the measurements to regularize the regression problem. However, in real-world solution reconstruction problems, the parameterized governing equation may be inconsistent with the physical phenomena that give rise to the measurement data. We show that due to assuming consistency between the true and parameterized physics, PINNs-based approaches may fail to satisfy three basic criteria of interpretability, robustness, and data consistency. As we argue, these criteria ensure that (i) the quality of the reconstruction can be assessed, (ii) the reconstruction does not depend strongly on the choice of physics loss, and (iii) that in certain situations, the physics parameters can be uniquely recovered. In the context of elasticity and heat transfer, we demonstrate how standard formulations of the physics loss and techniques for constraining the solution to respect the measurement data lead to different ``constraint forces" -- which we define as additional source terms arising from the constraints -- and that these constraint forces can significantly influence the reconstructed solution. To avoid the potentially substantial influence of the choice of physics loss and method of constraint enforcement on the reconstructed solution, we propose the ``explicit constraint force method'' (ECFM) to gain control of the source term introduced by the constraint. We then show that by satisfying the criteria of interpretability, robustness, and data consistency, this approach leads to more predictable and customizable reconstructions from noisy measurement data, even when the parameterization of the missing physics is inconsistent with the measured system.

Stochastic Subspace Descent Accelerated via Bi-fidelity Line Search

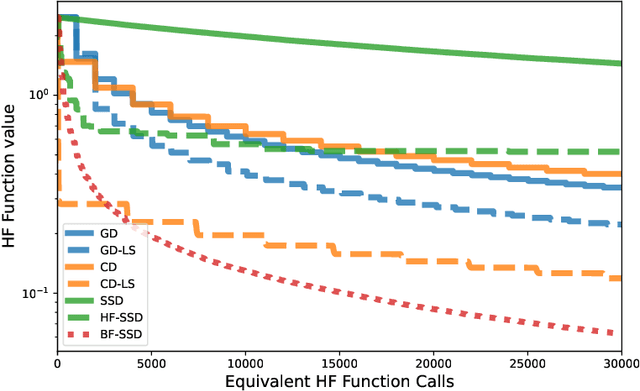
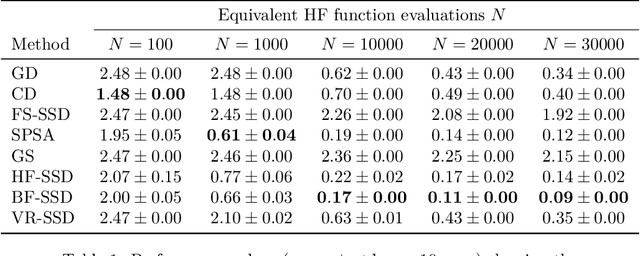
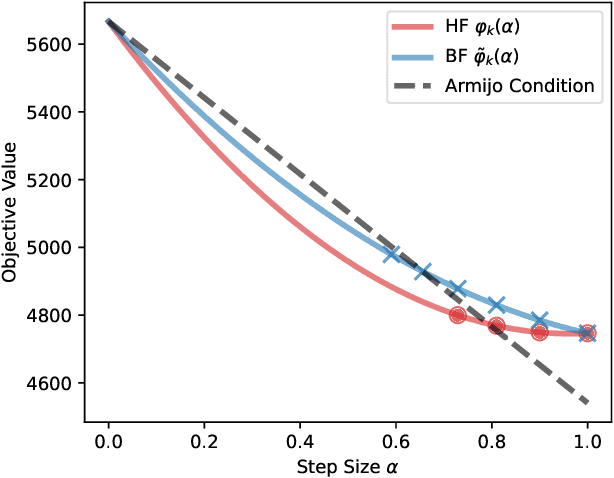
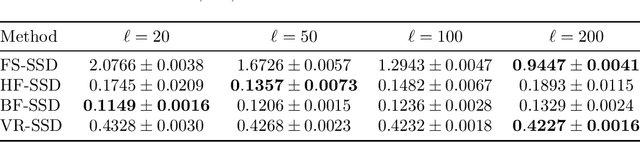
Efficient optimization remains a fundamental challenge across numerous scientific and engineering domains, especially when objective function and gradient evaluations are computationally expensive. While zeroth-order optimization methods offer effective approaches when gradients are inaccessible, their practical performance can be limited by the high cost associated with function queries. This work introduces the bi-fidelity stochastic subspace descent (BF-SSD) algorithm, a novel zeroth-order optimization method designed to reduce this computational burden. BF-SSD leverages a bi-fidelity framework, constructing a surrogate model from a combination of computationally inexpensive low-fidelity (LF) and accurate high-fidelity (HF) function evaluations. This surrogate model facilitates an efficient backtracking line search for step size selection, for which we provide theoretical convergence guarantees under standard assumptions. We perform a comprehensive empirical evaluation of BF-SSD across four distinct problems: a synthetic optimization benchmark, dual-form kernel ridge regression, black-box adversarial attacks on machine learning models, and transformer-based black-box language model fine-tuning. Numerical results demonstrate that BF-SSD consistently achieves superior optimization performance while requiring significantly fewer HF function evaluations compared to relevant baseline methods. This study highlights the efficacy of integrating bi-fidelity strategies within zeroth-order optimization, positioning BF-SSD as a promising and computationally efficient approach for tackling large-scale, high-dimensional problems encountered in various real-world applications.

Ensemble WSINDy for Data Driven Discovery of Governing Equations from Laser-based Full-field Measurements

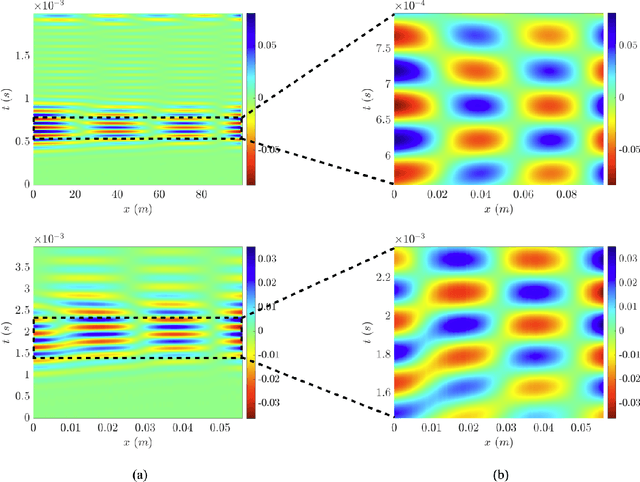
This work leverages laser vibrometry and the weak form of the sparse identification of nonlinear dynamics (WSINDy) for partial differential equations to learn macroscale governing equations from full-field experimental data. In the experiments, two beam-like specimens, one aluminum and one IDOX/Estane composite, are subjected to shear wave excitation in the low frequency regime and the response is measured in the form of particle velocity on the specimen surface. The WSINDy for PDEs algorithm is applied to the resulting spatio-temporal data to discover the effective dynamics of the specimens from a family of potential PDEs. The discovered PDE is of the recognizable Euler-Bernoulli beam model form, from which the Young's modulus for the two materials are estimated. An ensemble version of the WSINDy algorithm is also used which results in information about the uncertainty in the PDE coefficients and Young's moduli. The discovered PDEs are also simulated with a finite element code to compare against the experimental data with reasonable accuracy. Using full-field experimental data and WSINDy together is a powerful non-destructive approach for learning unknown governing equations and gaining insights about mechanical systems in the dynamic regime.

Constrained or Unconstrained? Neural-Network-Based Equation Discovery from Data

Throughout many fields, practitioners often rely on differential equations to model systems. Yet, for many applications, the theoretical derivation of such equations and/or accurate resolution of their solutions may be intractable. Instead, recently developed methods, including those based on parameter estimation, operator subset selection, and neural networks, allow for the data-driven discovery of both ordinary and partial differential equations (PDEs), on a spectrum of interpretability. The success of these strategies is often contingent upon the correct identification of representative equations from noisy observations of state variables and, as importantly and intertwined with that, the mathematical strategies utilized to enforce those equations. Specifically, the latter has been commonly addressed via unconstrained optimization strategies. Representing the PDE as a neural network, we propose to discover the PDE by solving a constrained optimization problem and using an intermediate state representation similar to a Physics-Informed Neural Network (PINN). The objective function of this constrained optimization problem promotes matching the data, while the constraints require that the PDE is satisfied at several spatial collocation points. We present a penalty method and a widely used trust-region barrier method to solve this constrained optimization problem, and we compare these methods on numerical examples. Our results on the Burgers' and the Korteweg-De Vreis equations demonstrate that the latter constrained method outperforms the penalty method, particularly for higher noise levels or fewer collocation points. For both methods, we solve these discovered neural network PDEs with classical methods, such as finite difference methods, as opposed to PINNs-type methods relying on automatic differentiation. We briefly highlight other small, yet crucial, implementation details.

PINN surrogate of Li-ion battery models for parameter inference. Part II: Regularization and application of the pseudo-2D model

Bayesian parameter inference is useful to improve Li-ion battery diagnostics and can help formulate battery aging models. However, it is computationally intensive and cannot be easily repeated for multiple cycles, multiple operating conditions, or multiple replicate cells. To reduce the computational cost of Bayesian calibration, numerical solvers for physics-based models can be replaced with faster surrogates. A physics-informed neural network (PINN) is developed as a surrogate for the pseudo-2D (P2D) battery model calibration. For the P2D surrogate, additional training regularization was needed as compared to the PINN single-particle model (SPM) developed in Part I. Both the PINN SPM and P2D surrogate models are exercised for parameter inference and compared to data obtained from a direct numerical solution of the governing equations. A parameter inference study highlights the ability to use these PINNs to calibrate scaling parameters for the cathode Li diffusion and the anode exchange current density. By realizing computational speed-ups of 2250x for the P2D model, as compared to using standard integrating methods, the PINN surrogates enable rapid state-of-health diagnostics. In the low-data availability scenario, the testing error was estimated to 2mV for the SPM surrogate and 10mV for the P2D surrogate which could be mitigated with additional data.

PINN surrogate of Li-ion battery models for parameter inference. Part I: Implementation and multi-fidelity hierarchies for the single-particle model

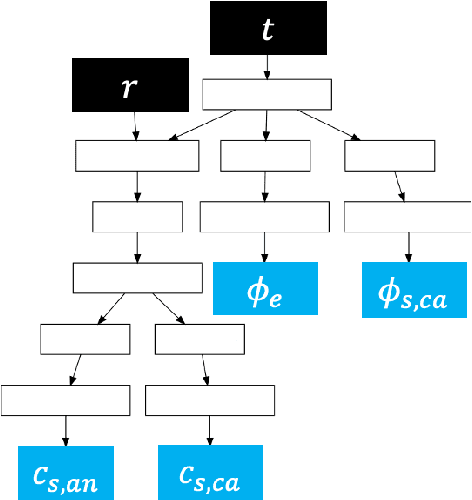
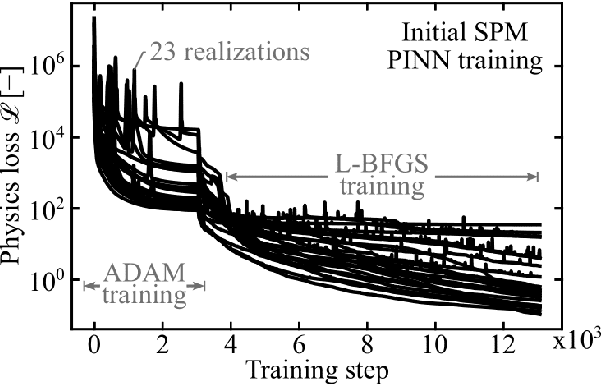
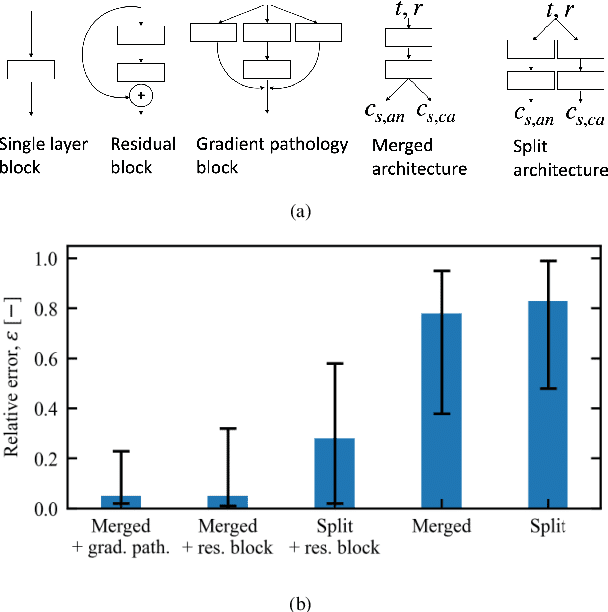
To plan and optimize energy storage demands that account for Li-ion battery aging dynamics, techniques need to be developed to diagnose battery internal states accurately and rapidly. This study seeks to reduce the computational resources needed to determine a battery's internal states by replacing physics-based Li-ion battery models -- such as the single-particle model (SPM) and the pseudo-2D (P2D) model -- with a physics-informed neural network (PINN) surrogate. The surrogate model makes high-throughput techniques, such as Bayesian calibration, tractable to determine battery internal parameters from voltage responses. This manuscript is the first of a two-part series that introduces PINN surrogates of Li-ion battery models for parameter inference (i.e., state-of-health diagnostics). In this first part, a method is presented for constructing a PINN surrogate of the SPM. A multi-fidelity hierarchical training, where several neural nets are trained with multiple physics-loss fidelities is shown to significantly improve the surrogate accuracy when only training on the governing equation residuals. The implementation is made available in a companion repository (https://github.com/NREL/pinnstripes). The techniques used to develop a PINN surrogate of the SPM are extended in Part II for the PINN surrogate for the P2D battery model, and explore the Bayesian calibration capabilities of both surrogates.

In Situ Framework for Coupling Simulation and Machine Learning with Application to CFD

Recent years have seen many successful applications of machine learning (ML) to facilitate fluid dynamic computations. As simulations grow, generating new training datasets for traditional offline learning creates I/O and storage bottlenecks. Additionally, performing inference at runtime requires non-trivial coupling of ML framework libraries with simulation codes. This work offers a solution to both limitations by simplifying this coupling and enabling in situ training and inference workflows on heterogeneous clusters. Leveraging SmartSim, the presented framework deploys a database to store data and ML models in memory, thus circumventing the file system. On the Polaris supercomputer, we demonstrate perfect scaling efficiency to the full machine size of the data transfer and inference costs thanks to a novel co-located deployment of the database. Moreover, we train an autoencoder in situ from a turbulent flow simulation, showing that the framework overhead is negligible relative to a solver time step and training epoch.

Bi-fidelity Variational Auto-encoder for Uncertainty Quantification

Quantifying the uncertainty of quantities of interest (QoIs) from physical systems is a primary objective in model validation. However, achieving this goal entails balancing the need for computational efficiency with the requirement for numerical accuracy. To address this trade-off, we propose a novel bi-fidelity formulation of variational auto-encoders (BF-VAE) designed to estimate the uncertainty associated with a QoI from low-fidelity (LF) and high-fidelity (HF) samples of the QoI. This model allows for the approximation of the statistics of the HF QoI by leveraging information derived from its LF counterpart. Specifically, we design a bi-fidelity auto-regressive model in the latent space that is integrated within the VAE's probabilistic encoder-decoder structure. An effective algorithm is proposed to maximize the variational lower bound of the HF log-likelihood in the presence of limited HF data, resulting in the synthesis of HF realizations with a reduced computational cost. Additionally, we introduce the concept of the bi-fidelity information bottleneck (BF-IB) to provide an information-theoretic interpretation of the proposed BF-VAE model. Our numerical results demonstrate that BF-VAE leads to considerably improved accuracy, as compared to a VAE trained using only HF data when limited HF data is available.