Continual Adversarial Reinforcement Learning (CARL) of False Data Injection detection: forgetting and explainability

False data injection attacks (FDIAs) on smart inverters are a growing concern linked to increased renewable energy production. While data-based FDIA detection methods are also actively developed, we show that they remain vulnerable to impactful and stealthy adversarial examples that can be crafted using Reinforcement Learning (RL). We propose to include such adversarial examples in data-based detection training procedure via a continual adversarial RL (CARL) approach. This way, one can pinpoint the deficiencies of data-based detection, thereby offering explainability during their incremental improvement. We show that a continual learning implementation is subject to catastrophic forgetting, and additionally show that forgetting can be addressed by employing a joint training strategy on all generated FDIA scenarios.

Detection of False Data Injection Attacks (FDIA) on Power Dynamical Systems With a State Prediction Method

With the deeper penetration of inverter-based resources in power systems, false data injection attacks (FDIA) are a growing cyber-security concern. They have the potential to disrupt the system's stability like frequency stability, thereby leading to catastrophic failures. Therefore, an FDIA detection method would be valuable to protect power systems. FDIAs typically induce a discrepancy between the desired and the effective behavior of the power system dynamics. A suitable detection method can leverage power dynamics predictions to identify whether such a discrepancy was induced by an FDIA. This work investigates the efficacy of temporal and spatio-temporal state prediction models, such as Long Short-Term Memory (LSTM) and a combination of Graph Neural Networks (GNN) with LSTM, for predicting frequency dynamics in the absence of an FDIA but with noisy measurements, and thereby identify FDIA events. For demonstration purposes, the IEEE 39 New England Kron-reduced model simulated with a swing equation is considered. It is shown that the proposed state prediction models can be used as a building block for developing an effective FDIA detection method that can maintain high detection accuracy across various attack and deployment settings. It is also shown how the FDIA detection should be deployed to limit its exposure to detection inaccuracies and mitigate its computational burden.

Discovery of False Data Injection Schemes on Frequency Controllers with Reinforcement Learning

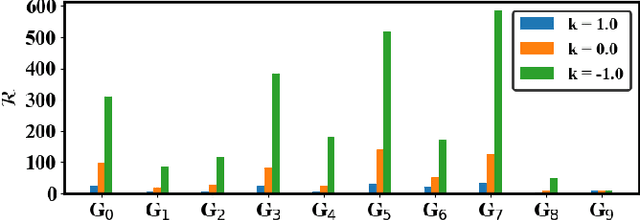
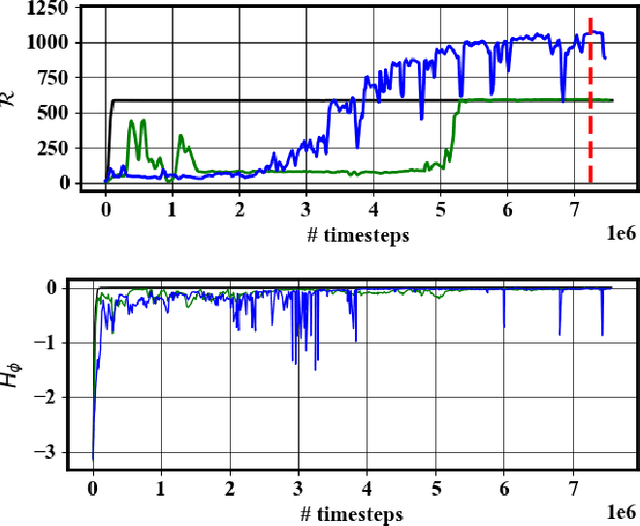
While inverter-based distributed energy resources (DERs) play a crucial role in integrating renewable energy into the power system, they concurrently diminish the grid's system inertia, elevating the risk of frequency instabilities. Furthermore, smart inverters, interfaced via communication networks, pose a potential vulnerability to cyber threats if not diligently managed. To proactively fortify the power grid against sophisticated cyber attacks, we propose to employ reinforcement learning (RL) to identify potential threats and system vulnerabilities. This study concentrates on analyzing adversarial strategies for false data injection, specifically targeting smart inverters involved in primary frequency control. Our findings demonstrate that an RL agent can adeptly discern optimal false data injection methods to manipulate inverter settings, potentially causing catastrophic consequences.

A Priori Uncertainty Quantification of Reacting Turbulence Closure Models using Bayesian Neural Networks

While many physics-based closure model forms have been posited for the sub-filter scale (SFS) in large eddy simulation (LES), vast amounts of data available from direct numerical simulation (DNS) create opportunities to leverage data-driven modeling techniques. Albeit flexible, data-driven models still depend on the dataset and the functional form of the model chosen. Increased adoption of such models requires reliable uncertainty estimates both in the data-informed and out-of-distribution regimes. In this work, we employ Bayesian neural networks (BNNs) to capture both epistemic and aleatoric uncertainties in a reacting flow model. In particular, we model the filtered progress variable scalar dissipation rate which plays a key role in the dynamics of turbulent premixed flames. We demonstrate that BNN models can provide unique insights about the structure of uncertainty of the data-driven closure models. We also propose a method for the incorporation of out-of-distribution information in a BNN. The efficacy of the model is demonstrated by a priori evaluation on a dataset consisting of a variety of flame conditions and fuels.

PINN surrogate of Li-ion battery models for parameter inference. Part I: Implementation and multi-fidelity hierarchies for the single-particle model

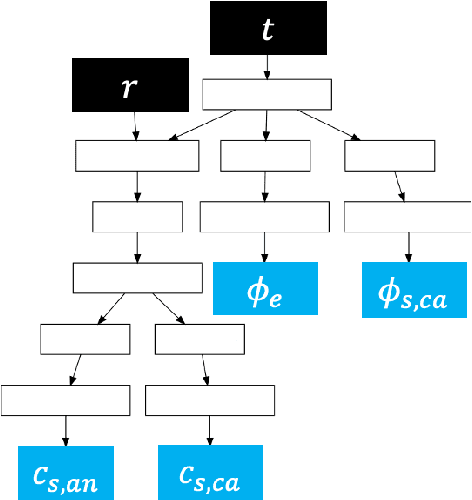
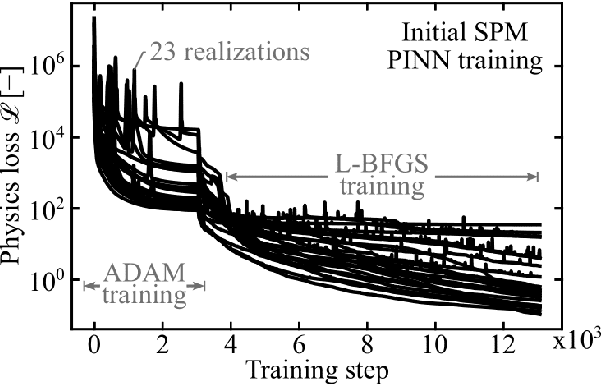
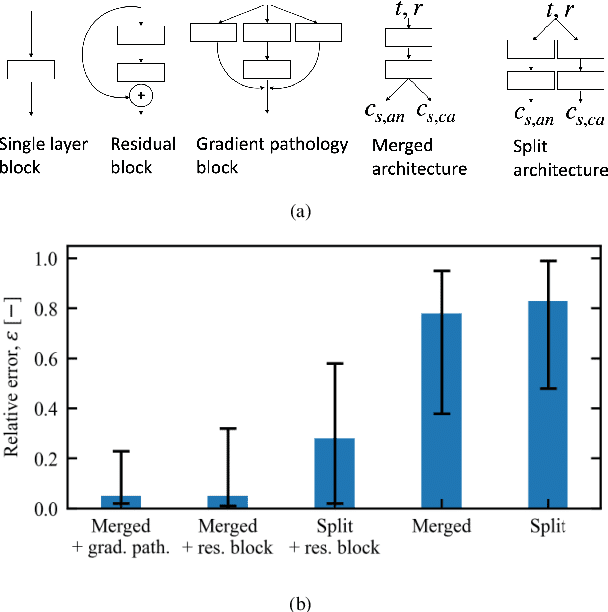
To plan and optimize energy storage demands that account for Li-ion battery aging dynamics, techniques need to be developed to diagnose battery internal states accurately and rapidly. This study seeks to reduce the computational resources needed to determine a battery's internal states by replacing physics-based Li-ion battery models -- such as the single-particle model (SPM) and the pseudo-2D (P2D) model -- with a physics-informed neural network (PINN) surrogate. The surrogate model makes high-throughput techniques, such as Bayesian calibration, tractable to determine battery internal parameters from voltage responses. This manuscript is the first of a two-part series that introduces PINN surrogates of Li-ion battery models for parameter inference (i.e., state-of-health diagnostics). In this first part, a method is presented for constructing a PINN surrogate of the SPM. A multi-fidelity hierarchical training, where several neural nets are trained with multiple physics-loss fidelities is shown to significantly improve the surrogate accuracy when only training on the governing equation residuals. The implementation is made available in a companion repository (https://github.com/NREL/pinnstripes). The techniques used to develop a PINN surrogate of the SPM are extended in Part II for the PINN surrogate for the P2D battery model, and explore the Bayesian calibration capabilities of both surrogates.

PINN surrogate of Li-ion battery models for parameter inference. Part II: Regularization and application of the pseudo-2D model

Bayesian parameter inference is useful to improve Li-ion battery diagnostics and can help formulate battery aging models. However, it is computationally intensive and cannot be easily repeated for multiple cycles, multiple operating conditions, or multiple replicate cells. To reduce the computational cost of Bayesian calibration, numerical solvers for physics-based models can be replaced with faster surrogates. A physics-informed neural network (PINN) is developed as a surrogate for the pseudo-2D (P2D) battery model calibration. For the P2D surrogate, additional training regularization was needed as compared to the PINN single-particle model (SPM) developed in Part I. Both the PINN SPM and P2D surrogate models are exercised for parameter inference and compared to data obtained from a direct numerical solution of the governing equations. A parameter inference study highlights the ability to use these PINNs to calibrate scaling parameters for the cathode Li diffusion and the anode exchange current density. By realizing computational speed-ups of 2250x for the P2D model, as compared to using standard integrating methods, the PINN surrogates enable rapid state-of-health diagnostics. In the low-data availability scenario, the testing error was estimated to 2mV for the SPM surrogate and 10mV for the P2D surrogate which could be mitigated with additional data.

Generating Initial Conditions for Ensemble Data Assimilation of Large-Eddy Simulations with Latent Diffusion Models

In order to accurately reconstruct the time history of the atmospheric state, ensemble-based data assimilation algorithms need to be initialized appropriately. At present, there is no standard approach to initializing large-eddy simulation codes for microscale data assimilation. Here, given synthetic observations, we generate ensembles of plausible initial conditions using a latent diffusion model. We modify the original, two-dimensional latent diffusion model code to work on three-dimensional turbulent fields. The algorithm produces realistic and diverse samples that successfully run when inserted into a large-eddy simulation code. The samples have physically plausible turbulent structures on large and moderate spatial scales in the context of our simulations. The generated ensembles show a lower spread in the vicinity of observations while having higher variability further from the observations, matching expected behavior. Ensembles demonstrate near-zero bias relative to ground truth in the vicinity of observations, but rank histogram analysis suggests that ensembles have too little member-to-member variability when compared to an ideal ensemble. Given the success of the latent diffusion model, the generated ensembles will be tested in their ability to recreate a time history of the atmosphere when coupled to an ensemble-based data assimilation algorithm in upcoming work. We find that diffusion models show promise and potential for other applications within the geosciences.

Bi-fidelity Modeling of Uncertain and Partially Unknown Systems using DeepONets

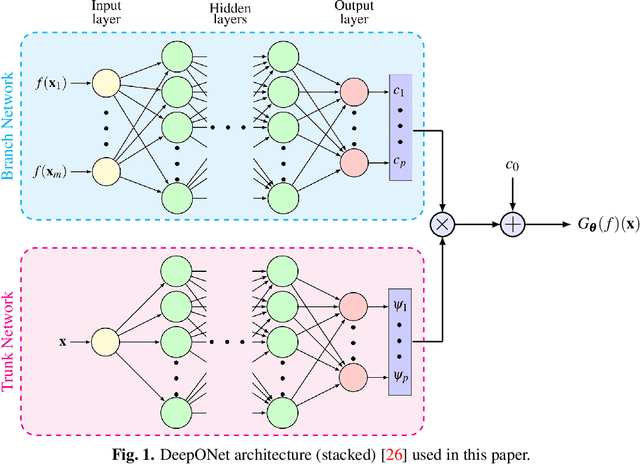
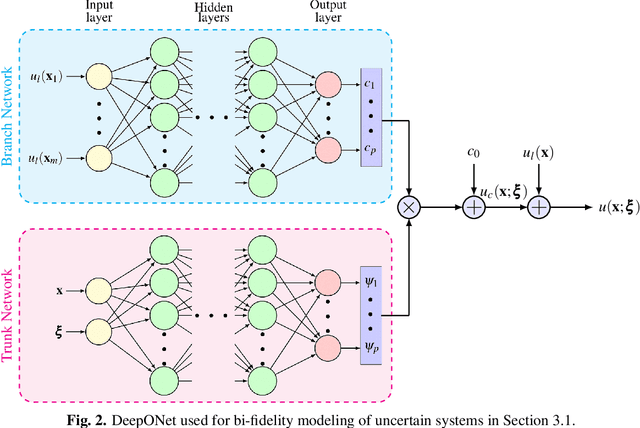
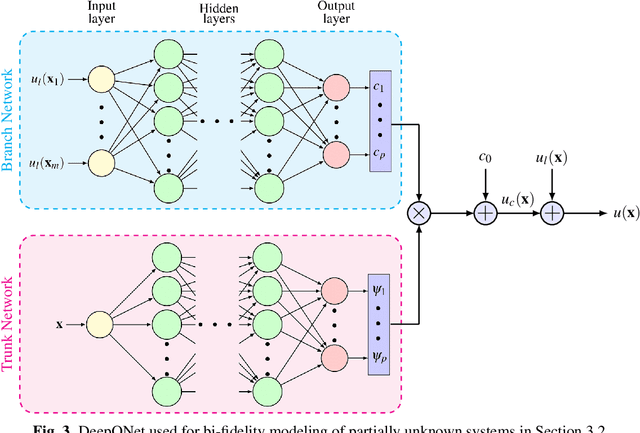
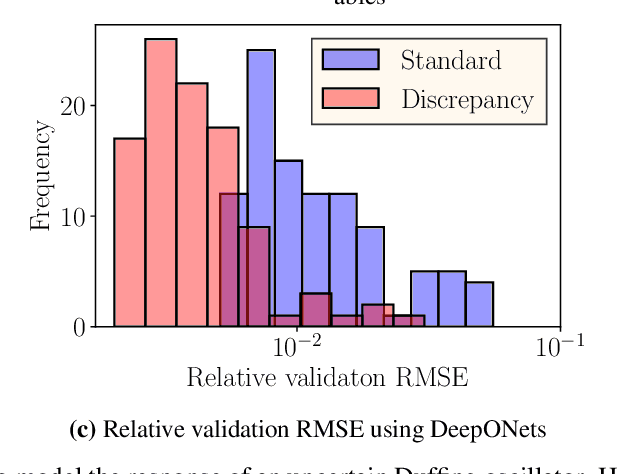
Recent advances in modeling large-scale complex physical systems have shifted research focuses towards data-driven techniques. However, generating datasets by simulating complex systems can require significant computational resources. Similarly, acquiring experimental datasets can prove difficult as well. For these systems, often computationally inexpensive, but in general inaccurate, models, known as the low-fidelity models, are available. In this paper, we propose a bi-fidelity modeling approach for complex physical systems, where we model the discrepancy between the true system's response and low-fidelity response in the presence of a small training dataset from the true system's response using a deep operator network (DeepONet), a neural network architecture suitable for approximating nonlinear operators. We apply the approach to model systems that have parametric uncertainty and are partially unknown. Three numerical examples are used to show the efficacy of the proposed approach to model uncertain and partially unknown complex physical systems.

Uniform-in-Phase-Space Data Selection with Iterative Normalizing Flows

Improvements in computational and experimental capabilities are rapidly increasing the amount of scientific data that is routinely generated. In applications that are constrained by memory and computational intensity, excessively large datasets may hinder scientific discovery, making data reduction a critical component of data-driven methods. Datasets are growing in two directions: the number of data points and their dimensionality. Whereas data compression techniques are concerned with reducing dimensionality, the focus here is on reducing the number of data points. A strategy is proposed to select data points such that they uniformly span the phase-space of the data. The algorithm proposed relies on estimating the probability map of the data and using it to construct an acceptance probability. An iterative method is used to accurately estimate the probability of the rare data points when only a small subset of the dataset is used to construct the probability map. Instead of binning the phase-space to estimate the probability map, its functional form is approximated with a normalizing flow. Therefore, the method naturally extends to high-dimensional datasets. The proposed framework is demonstrated as a viable pathway to enable data-efficient machine learning when abundant data is available. An implementation of the method is available in a companion repository (https://github.com/NREL/Phase-space-sampling).

GANISP: a GAN-assisted Importance SPlitting Probability Estimator

Designing manufacturing processes with high yield and strong reliability relies on effective methods for rare event estimation. Genealogical importance splitting reduces the variance of rare event probability estimators by iteratively selecting and replicating realizations that are headed towards a rare event. The replication step is difficult when applied to deterministic systems where the initial conditions of the offspring realizations need to be modified. Typically, a random perturbation is applied to the offspring to differentiate their trajectory from the parent realization. However, this random perturbation strategy may be effective for some systems while failing for others, preventing variance reduction in the probability estimate. This work seeks to address this limitation using a generative model such as a Generative Adversarial Network (GAN) to generate perturbations that are consistent with the attractor of the dynamical system. The proposed GAN-assisted Importance SPlitting method (GANISP) improves the variance reduction for the system targeted. An implementation of the method is available in a companion repository (https://github.com/NREL/GANISP).