Continual Adversarial Reinforcement Learning (CARL) of False Data Injection detection: forgetting and explainability

False data injection attacks (FDIAs) on smart inverters are a growing concern linked to increased renewable energy production. While data-based FDIA detection methods are also actively developed, we show that they remain vulnerable to impactful and stealthy adversarial examples that can be crafted using Reinforcement Learning (RL). We propose to include such adversarial examples in data-based detection training procedure via a continual adversarial RL (CARL) approach. This way, one can pinpoint the deficiencies of data-based detection, thereby offering explainability during their incremental improvement. We show that a continual learning implementation is subject to catastrophic forgetting, and additionally show that forgetting can be addressed by employing a joint training strategy on all generated FDIA scenarios.

Detection of False Data Injection Attacks (FDIA) on Power Dynamical Systems With a State Prediction Method

With the deeper penetration of inverter-based resources in power systems, false data injection attacks (FDIA) are a growing cyber-security concern. They have the potential to disrupt the system's stability like frequency stability, thereby leading to catastrophic failures. Therefore, an FDIA detection method would be valuable to protect power systems. FDIAs typically induce a discrepancy between the desired and the effective behavior of the power system dynamics. A suitable detection method can leverage power dynamics predictions to identify whether such a discrepancy was induced by an FDIA. This work investigates the efficacy of temporal and spatio-temporal state prediction models, such as Long Short-Term Memory (LSTM) and a combination of Graph Neural Networks (GNN) with LSTM, for predicting frequency dynamics in the absence of an FDIA but with noisy measurements, and thereby identify FDIA events. For demonstration purposes, the IEEE 39 New England Kron-reduced model simulated with a swing equation is considered. It is shown that the proposed state prediction models can be used as a building block for developing an effective FDIA detection method that can maintain high detection accuracy across various attack and deployment settings. It is also shown how the FDIA detection should be deployed to limit its exposure to detection inaccuracies and mitigate its computational burden.

Unsupervised Deep Learning for AC Optimal Power Flow via Lagrangian Duality

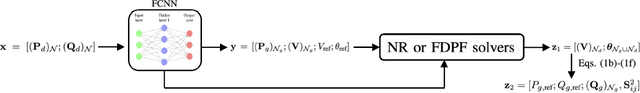
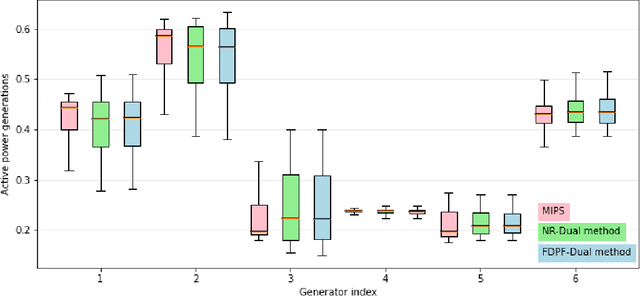
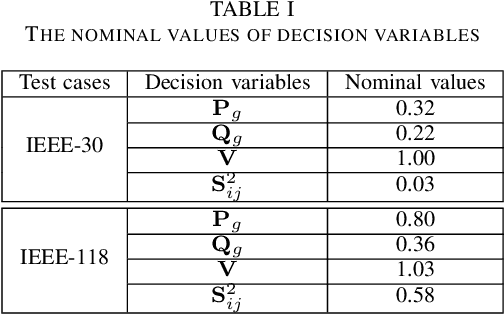
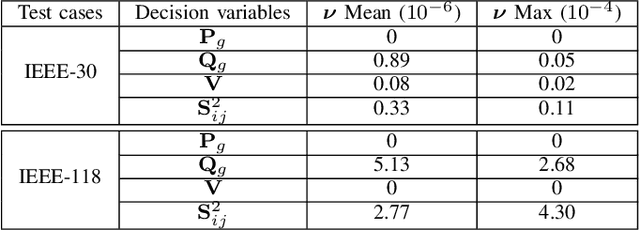
Non-convex AC optimal power flow (AC-OPF) is a fundamental optimization problem in power system analysis. The computational complexity of conventional solvers is typically high and not suitable for large-scale networks in real-time operation. Hence, deep learning based approaches have gained intensive attention to conduct the time-consuming training process offline. Supervised learning methods may yield a feasible AC-OPF solution with a small optimality gap. However, they often need conventional solvers to generate the training dataset. This paper proposes an end-to-end unsupervised learning based framework for AC-OPF. We develop a deep neural network to output a partial set of decision variables while the remaining variables are recovered by solving AC power flow equations. The fast decoupled power flow solver is adopted to further reduce the computational time. In addition, we propose using a modified augmented Lagrangian function as the training loss. The multipliers are adjusted dynamically based on the degree of constraint violation. Extensive numerical test results corroborate the advantages of our proposed approach over some existing methods.