Alpha-VI DeepONet: A prior-robust variational Bayesian approach for enhancing DeepONets with uncertainty quantification

We introduce a novel deep operator network (DeepONet) framework that incorporates generalised variational inference (GVI) using R\'enyi's $\alpha$-divergence to learn complex operators while quantifying uncertainty. By incorporating Bayesian neural networks as the building blocks for the branch and trunk networks, our framework endows DeepONet with uncertainty quantification. The use of R\'enyi's $\alpha$-divergence, instead of the Kullback-Leibler divergence (KLD), commonly used in standard variational inference, mitigates issues related to prior misspecification that are prevalent in Variational Bayesian DeepONets. This approach offers enhanced flexibility and robustness. We demonstrate that modifying the variational objective function yields superior results in terms of minimising the mean squared error and improving the negative log-likelihood on the test set. Our framework's efficacy is validated across various mechanical systems, where it outperforms both deterministic and standard KLD-based VI DeepONets in predictive accuracy and uncertainty quantification. The hyperparameter $\alpha$, which controls the degree of robustness, can be tuned to optimise performance for specific problems. We apply this approach to a range of mechanics problems, including gravity pendulum, advection-diffusion, and diffusion-reaction systems. Our findings underscore the potential of $\alpha$-VI DeepONet to advance the field of data-driven operator learning and its applications in engineering and scientific domains.

PINN surrogate of Li-ion battery models for parameter inference. Part II: Regularization and application of the pseudo-2D model

Bayesian parameter inference is useful to improve Li-ion battery diagnostics and can help formulate battery aging models. However, it is computationally intensive and cannot be easily repeated for multiple cycles, multiple operating conditions, or multiple replicate cells. To reduce the computational cost of Bayesian calibration, numerical solvers for physics-based models can be replaced with faster surrogates. A physics-informed neural network (PINN) is developed as a surrogate for the pseudo-2D (P2D) battery model calibration. For the P2D surrogate, additional training regularization was needed as compared to the PINN single-particle model (SPM) developed in Part I. Both the PINN SPM and P2D surrogate models are exercised for parameter inference and compared to data obtained from a direct numerical solution of the governing equations. A parameter inference study highlights the ability to use these PINNs to calibrate scaling parameters for the cathode Li diffusion and the anode exchange current density. By realizing computational speed-ups of 2250x for the P2D model, as compared to using standard integrating methods, the PINN surrogates enable rapid state-of-health diagnostics. In the low-data availability scenario, the testing error was estimated to 2mV for the SPM surrogate and 10mV for the P2D surrogate which could be mitigated with additional data.

PINN surrogate of Li-ion battery models for parameter inference. Part I: Implementation and multi-fidelity hierarchies for the single-particle model

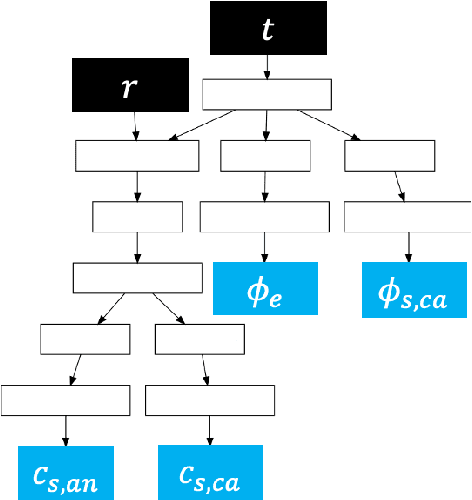
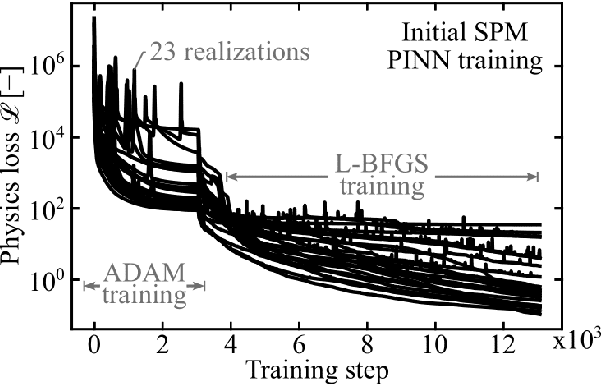
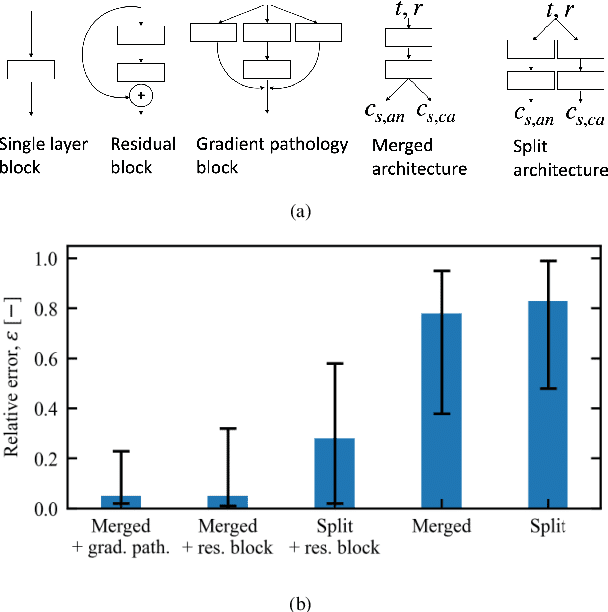
To plan and optimize energy storage demands that account for Li-ion battery aging dynamics, techniques need to be developed to diagnose battery internal states accurately and rapidly. This study seeks to reduce the computational resources needed to determine a battery's internal states by replacing physics-based Li-ion battery models -- such as the single-particle model (SPM) and the pseudo-2D (P2D) model -- with a physics-informed neural network (PINN) surrogate. The surrogate model makes high-throughput techniques, such as Bayesian calibration, tractable to determine battery internal parameters from voltage responses. This manuscript is the first of a two-part series that introduces PINN surrogates of Li-ion battery models for parameter inference (i.e., state-of-health diagnostics). In this first part, a method is presented for constructing a PINN surrogate of the SPM. A multi-fidelity hierarchical training, where several neural nets are trained with multiple physics-loss fidelities is shown to significantly improve the surrogate accuracy when only training on the governing equation residuals. The implementation is made available in a companion repository (https://github.com/NREL/pinnstripes). The techniques used to develop a PINN surrogate of the SPM are extended in Part II for the PINN surrogate for the P2D battery model, and explore the Bayesian calibration capabilities of both surrogates.

A Bi-fidelity DeepONet Approach for Modeling Uncertain and Degrading Hysteretic Systems

Nonlinear systems, such as with degrading hysteretic behavior, are often encountered in engineering applications. In addition, due to the ubiquitous presence of uncertainty and the modeling of such systems becomes increasingly difficult. On the other hand, datasets from pristine models developed without knowing the nature of the degrading effects can be easily obtained. In this paper, we use datasets from pristine models without considering the degrading effects of hysteretic systems as low-fidelity representations that capture many of the important characteristics of the true system's behavior to train a deep operator network (DeepONet). Three numerical examples are used to show that the proposed use of the DeepONets to model the discrepancies between the low-fidelity model and the true system's response leads to significant improvements in the prediction error in the presence of uncertainty in the model parameters for degrading hysteretic systems.

Bi-fidelity Modeling of Uncertain and Partially Unknown Systems using DeepONets

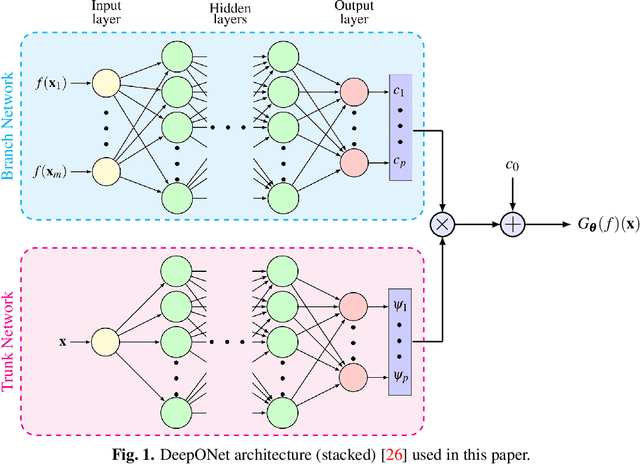
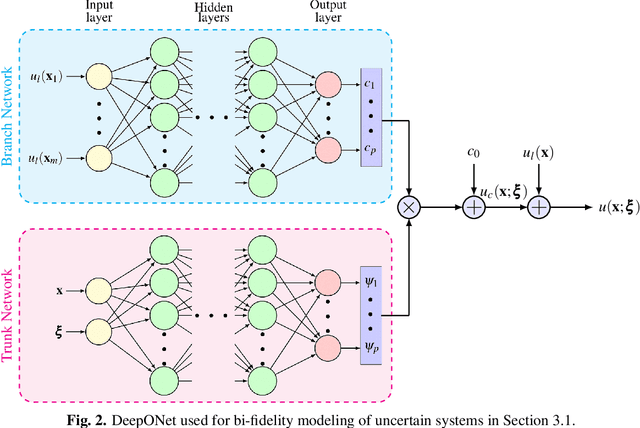
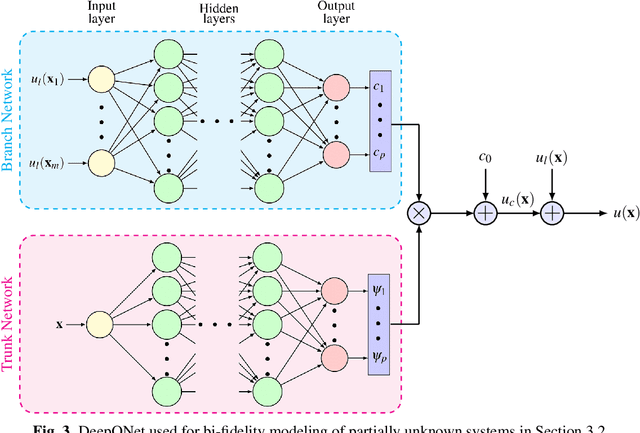
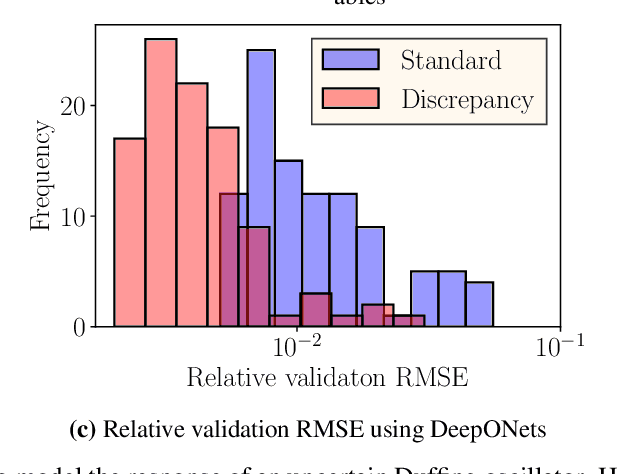
Recent advances in modeling large-scale complex physical systems have shifted research focuses towards data-driven techniques. However, generating datasets by simulating complex systems can require significant computational resources. Similarly, acquiring experimental datasets can prove difficult as well. For these systems, often computationally inexpensive, but in general inaccurate, models, known as the low-fidelity models, are available. In this paper, we propose a bi-fidelity modeling approach for complex physical systems, where we model the discrepancy between the true system's response and low-fidelity response in the presence of a small training dataset from the true system's response using a deep operator network (DeepONet), a neural network architecture suitable for approximating nonlinear operators. We apply the approach to model systems that have parametric uncertainty and are partially unknown. Three numerical examples are used to show the efficacy of the proposed approach to model uncertain and partially unknown complex physical systems.

Neural Network Training Using $\ell_1$-Regularization and Bi-fidelity Data

With the capability of accurately representing a functional relationship between the inputs of a physical system's model and output quantities of interest, neural networks have become popular for surrogate modeling in scientific applications. However, as these networks are over-parameterized, their training often requires a large amount of data. To prevent overfitting and improve generalization error, regularization based on, e.g., $\ell_1$- and $\ell_2$-norms of the parameters is applied. Similarly, multiple connections of the network may be pruned to increase sparsity in the network parameters. In this paper, we explore the effects of sparsity promoting $\ell_1$-regularization on training neural networks when only a small training dataset from a high-fidelity model is available. As opposed to standard $\ell_1$-regularization that is known to be inadequate, we consider two variants of $\ell_1$-regularization informed by the parameters of an identical network trained using data from lower-fidelity models of the problem at hand. These bi-fidelity strategies are generalizations of transfer learning of neural networks that uses the parameters learned from a large low-fidelity dataset to efficiently train networks for a small high-fidelity dataset. We also compare the bi-fidelity strategies with two $\ell_1$-regularization methods that only use the high-fidelity dataset. Three numerical examples for propagating uncertainty through physical systems are used to show that the proposed bi-fidelity $\ell_1$-regularization strategies produce errors that are one order of magnitude smaller than those of networks trained only using datasets from the high-fidelity models.

Uncertainty Quantification of Locally Nonlinear Dynamical Systems using Neural Networks

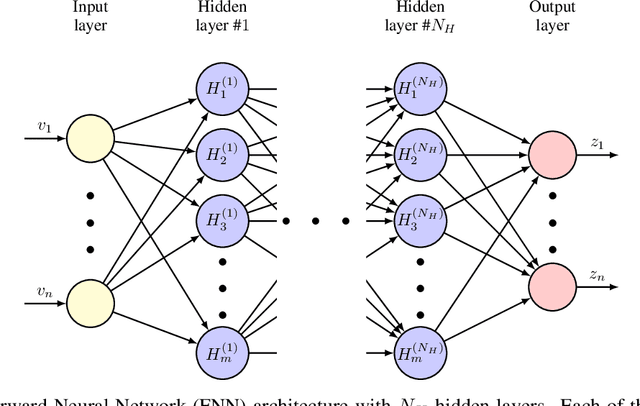
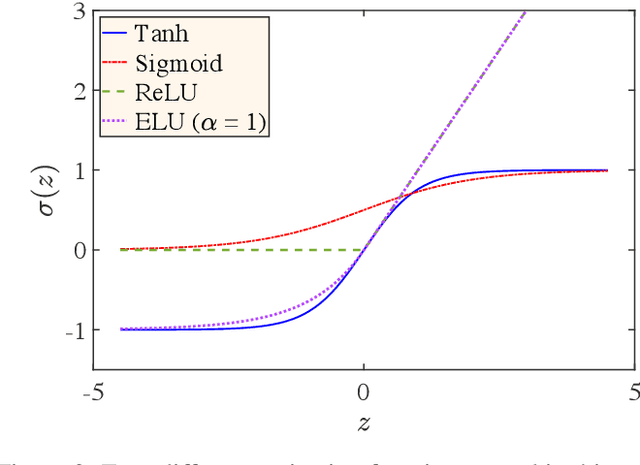
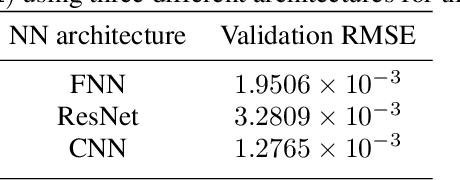
Models are often given in terms of differential equations to represent physical systems. In the presence of uncertainty, accurate prediction of the behavior of these systems using the models requires understanding the effect of uncertainty in the response. In uncertainty quantification, statistics such as mean and variance of the response of these physical systems are sought. To estimate these statistics sampling-based methods like Monte Carlo often require many evaluations of the models' governing equations for multiple realizations of the uncertainty. However, for large complex engineering systems, these methods become computationally burdensome. In structural engineering, often an otherwise linear structure contains spatially local nonlinearities with uncertainty present in them. A standard nonlinear solver for them with sampling-based methods for uncertainty quantification incurs significant computational cost for estimating the statistics of the response. To ease this computational burden of uncertainty quantification of large-scale locally nonlinear dynamical systems, a method is proposed herein, which decomposes the response into two parts -- response of a nominal linear system and a corrective term. This corrective term is the response from a pseudoforce that contains the nonlinearity and uncertainty information. In this paper, neural network, a recently popular tool for universal function approximation in the scientific machine learning community due to the advancement of computational capability as well as the availability of open-sourced packages like PyTorch and TensorFlow is used to estimate the pseudoforce. Since only the nonlinear and uncertain pseudoforce is modeled using the neural networks the same network can be used to predict a different response of the system and hence no new network is required to train if the statistic of a different response is sought.

On transfer learning of neural networks using bi-fidelity data for uncertainty propagation

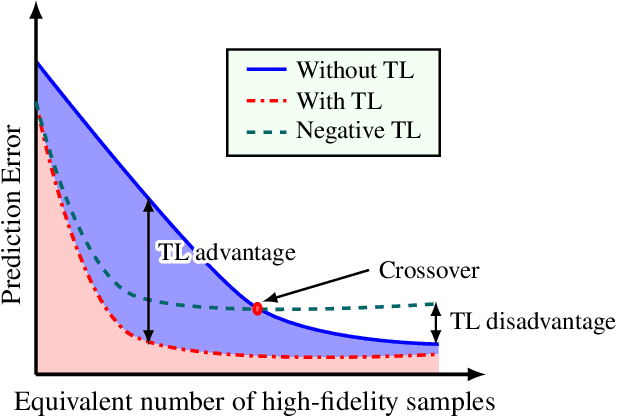
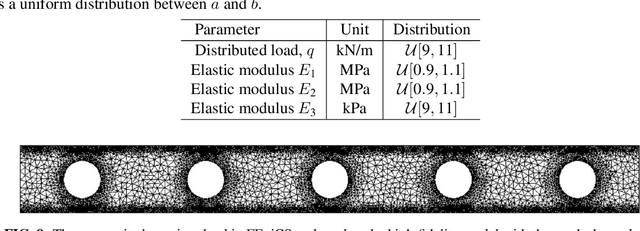
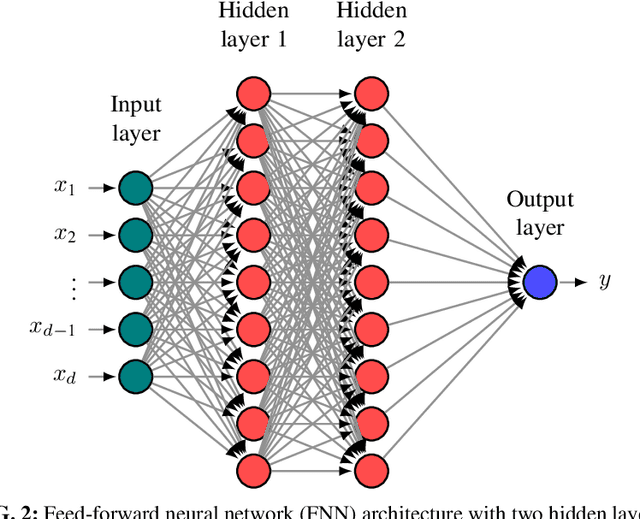
Due to their high degree of expressiveness, neural networks have recently been used as surrogate models for mapping inputs of an engineering system to outputs of interest. Once trained, neural networks are computationally inexpensive to evaluate and remove the need for repeated evaluations of computationally expensive models in uncertainty quantification applications. However, given the highly parameterized construction of neural networks, especially deep neural networks, accurate training often requires large amounts of simulation data that may not be available in the case of computationally expensive systems. In this paper, to alleviate this issue for uncertainty propagation, we explore the application of transfer learning techniques using training data generated from both high- and low-fidelity models. We explore two strategies for coupling these two datasets during the training procedure, namely, the standard transfer learning and the bi-fidelity weighted learning. In the former approach, a neural network model mapping the inputs to the outputs of interest is trained based on the low-fidelity data. The high-fidelity data is then used to adapt the parameters of the upper layer(s) of the low-fidelity network, or train a simpler neural network to map the output of the low-fidelity network to that of the high-fidelity model. In the latter approach, the entire low-fidelity network parameters are updated using data generated via a Gaussian process model trained with a small high-fidelity dataset. The parameter updates are performed via a variant of stochastic gradient descent with learning rates given by the Gaussian process model. Using three numerical examples, we illustrate the utility of these bi-fidelity transfer learning methods where we focus on accuracy improvement achieved by transfer learning over standard training approaches.