Super Resolution for Renewable Energy Resource Data With Wind From Reanalysis Data (Sup3rWind) and Application to Ukraine

With an increasing share of the electricity grid relying on wind to provide generating capacity and energy, there is an expanding global need for historically accurate high-resolution wind data. Conventional downscaling methods for generating these data have a high computational burden and require extensive tuning for historical accuracy. In this work, we present a novel deep learning-based spatiotemporal downscaling method, using generative adversarial networks (GANs), for generating historically accurate high-resolution wind resource data from the European Centre for Medium-Range Weather Forecasting Reanalysis version 5 data (ERA5). We achieve results comparable in historical accuracy and spatiotemporal variability to conventional downscaling by training a GAN model with ERA5 low-resolution input and high-resolution targets from the Wind Integration National Dataset, while reducing computational costs over dynamical downscaling by two orders of magnitude. Spatiotemporal cross-validation shows low error and high correlations with observations and excellent agreement with holdout data across distributions of physical metrics. We apply this approach to downscale 30-km hourly ERA5 data to 2-km 5-minute wind data for January 2000 through December 2023 at multiple hub heights over Eastern Europe. Uncertainty is estimated over the period with observational data by additionally downscaling the members of the European Centre for Medium-Range Weather Forecasting Ensemble of Data Assimilations. Comparisons against observational data from the Meteorological Assimilation Data Ingest System and multiple wind farms show comparable performance to the CONUS validation. This 24-year data record is the first member of the super resolution for renewable energy resource data with wind from reanalysis data dataset (Sup3rWind).

PINN surrogate of Li-ion battery models for parameter inference. Part II: Regularization and application of the pseudo-2D model

Bayesian parameter inference is useful to improve Li-ion battery diagnostics and can help formulate battery aging models. However, it is computationally intensive and cannot be easily repeated for multiple cycles, multiple operating conditions, or multiple replicate cells. To reduce the computational cost of Bayesian calibration, numerical solvers for physics-based models can be replaced with faster surrogates. A physics-informed neural network (PINN) is developed as a surrogate for the pseudo-2D (P2D) battery model calibration. For the P2D surrogate, additional training regularization was needed as compared to the PINN single-particle model (SPM) developed in Part I. Both the PINN SPM and P2D surrogate models are exercised for parameter inference and compared to data obtained from a direct numerical solution of the governing equations. A parameter inference study highlights the ability to use these PINNs to calibrate scaling parameters for the cathode Li diffusion and the anode exchange current density. By realizing computational speed-ups of 2250x for the P2D model, as compared to using standard integrating methods, the PINN surrogates enable rapid state-of-health diagnostics. In the low-data availability scenario, the testing error was estimated to 2mV for the SPM surrogate and 10mV for the P2D surrogate which could be mitigated with additional data.

PINN surrogate of Li-ion battery models for parameter inference. Part I: Implementation and multi-fidelity hierarchies for the single-particle model

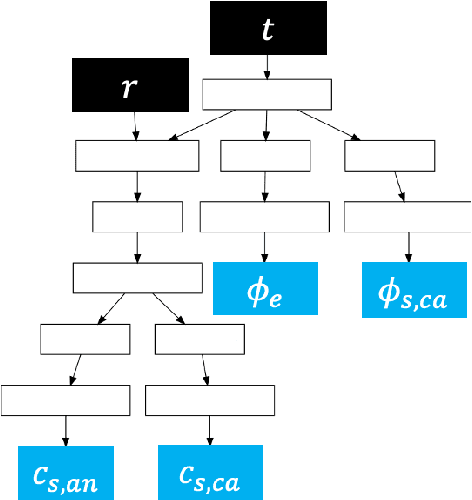
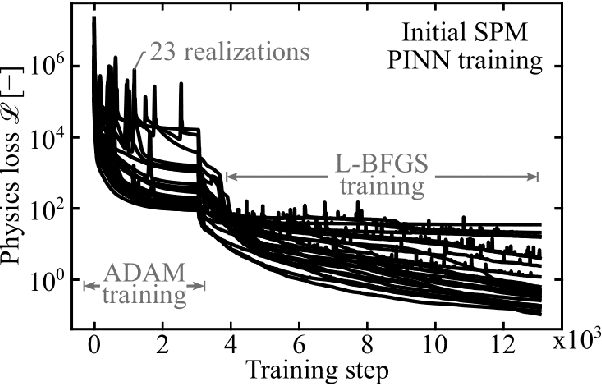
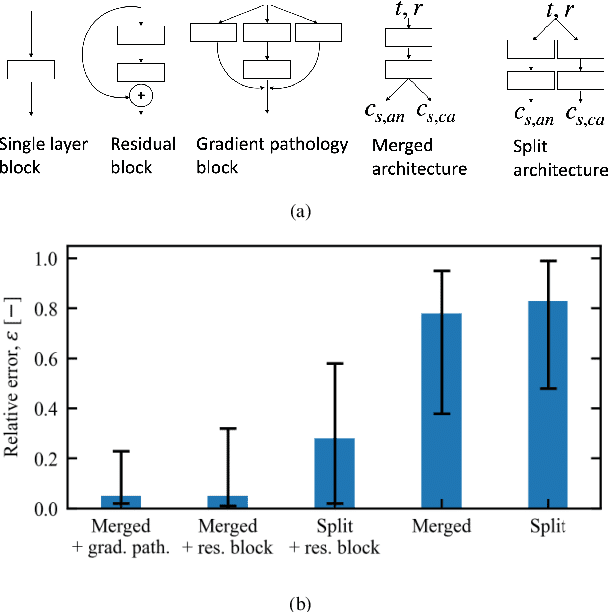
To plan and optimize energy storage demands that account for Li-ion battery aging dynamics, techniques need to be developed to diagnose battery internal states accurately and rapidly. This study seeks to reduce the computational resources needed to determine a battery's internal states by replacing physics-based Li-ion battery models -- such as the single-particle model (SPM) and the pseudo-2D (P2D) model -- with a physics-informed neural network (PINN) surrogate. The surrogate model makes high-throughput techniques, such as Bayesian calibration, tractable to determine battery internal parameters from voltage responses. This manuscript is the first of a two-part series that introduces PINN surrogates of Li-ion battery models for parameter inference (i.e., state-of-health diagnostics). In this first part, a method is presented for constructing a PINN surrogate of the SPM. A multi-fidelity hierarchical training, where several neural nets are trained with multiple physics-loss fidelities is shown to significantly improve the surrogate accuracy when only training on the governing equation residuals. The implementation is made available in a companion repository (https://github.com/NREL/pinnstripes). The techniques used to develop a PINN surrogate of the SPM are extended in Part II for the PINN surrogate for the P2D battery model, and explore the Bayesian calibration capabilities of both surrogates.

Bi-fidelity Modeling of Uncertain and Partially Unknown Systems using DeepONets

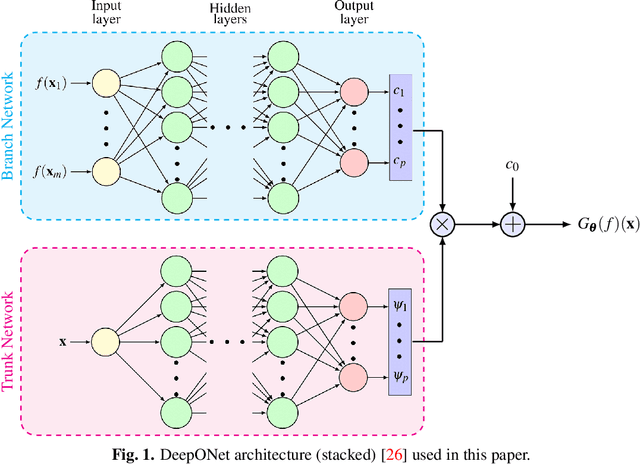
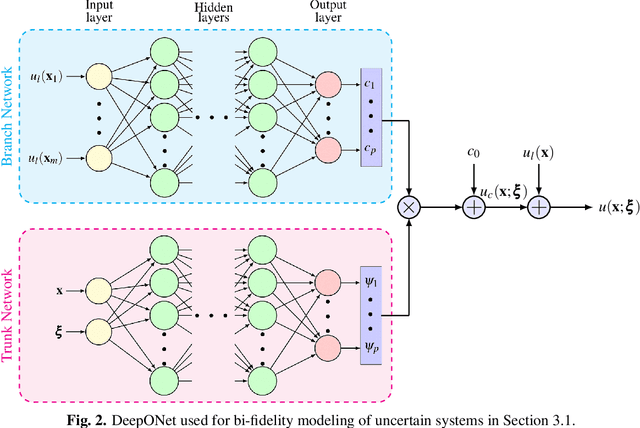
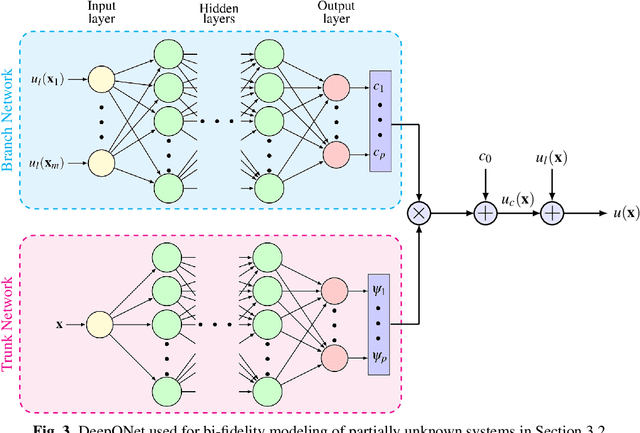
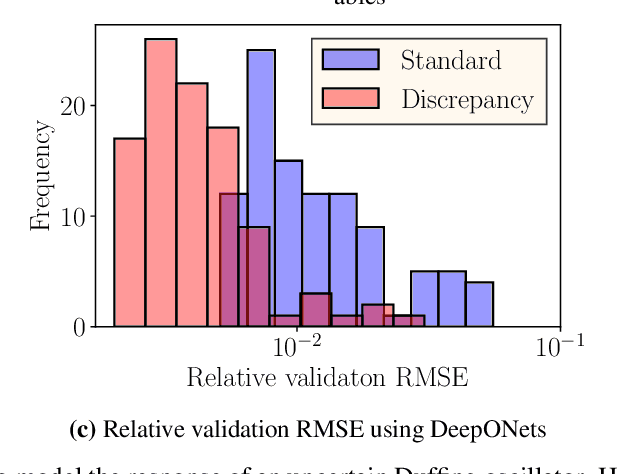
Recent advances in modeling large-scale complex physical systems have shifted research focuses towards data-driven techniques. However, generating datasets by simulating complex systems can require significant computational resources. Similarly, acquiring experimental datasets can prove difficult as well. For these systems, often computationally inexpensive, but in general inaccurate, models, known as the low-fidelity models, are available. In this paper, we propose a bi-fidelity modeling approach for complex physical systems, where we model the discrepancy between the true system's response and low-fidelity response in the presence of a small training dataset from the true system's response using a deep operator network (DeepONet), a neural network architecture suitable for approximating nonlinear operators. We apply the approach to model systems that have parametric uncertainty and are partially unknown. Three numerical examples are used to show the efficacy of the proposed approach to model uncertain and partially unknown complex physical systems.

GANISP: a GAN-assisted Importance SPlitting Probability Estimator

Designing manufacturing processes with high yield and strong reliability relies on effective methods for rare event estimation. Genealogical importance splitting reduces the variance of rare event probability estimators by iteratively selecting and replicating realizations that are headed towards a rare event. The replication step is difficult when applied to deterministic systems where the initial conditions of the offspring realizations need to be modified. Typically, a random perturbation is applied to the offspring to differentiate their trajectory from the parent realization. However, this random perturbation strategy may be effective for some systems while failing for others, preventing variance reduction in the probability estimate. This work seeks to address this limitation using a generative model such as a Generative Adversarial Network (GAN) to generate perturbations that are consistent with the attractor of the dynamical system. The proposed GAN-assisted Importance SPlitting method (GANISP) improves the variance reduction for the system targeted. An implementation of the method is available in a companion repository (https://github.com/NREL/GANISP).

Adversarial sampling of unknown and high-dimensional conditional distributions

Many engineering problems require the prediction of realization-to-realization variability or a refined description of modeled quantities. In that case, it is necessary to sample elements from unknown high-dimensional spaces with possibly millions of degrees of freedom. While there exist methods able to sample elements from probability density functions (PDF) with known shapes, several approximations need to be made when the distribution is unknown. In this paper the sampling method, as well as the inference of the underlying distribution, are both handled with a data-driven method known as generative adversarial networks (GAN), which trains two competing neural networks to produce a network that can effectively generate samples from the training set distribution. In practice, it is often necessary to draw samples from conditional distributions. When the conditional variables are continuous, only one (if any) data point corresponding to a particular value of a conditioning variable may be available, which is not sufficient to estimate the conditional distribution. This work handles this problem using an a priori estimation of the conditional moments of a PDF. Two approaches, stochastic estimation, and an external neural network are compared here for computing these moments; however, any preferred method can be used. The algorithm is demonstrated in the case of the deconvolution of a filtered turbulent flow field. It is shown that all the versions of the proposed algorithm effectively sample the target conditional distribution with minimal impact on the quality of the samples compared to state-of-the-art methods. Additionally, the procedure can be used as a metric for the diversity of samples generated by a conditional GAN (cGAN) conditioned with continuous variables.