Towards Gaussian Process for operator learning: an uncertainty aware resolution independent operator learning algorithm for computational mechanics

The growing demand for accurate, efficient, and scalable solutions in computational mechanics highlights the need for advanced operator learning algorithms that can efficiently handle large datasets while providing reliable uncertainty quantification. This paper introduces a novel Gaussian Process (GP) based neural operator for solving parametric differential equations. The approach proposed leverages the expressive capability of deterministic neural operators and the uncertainty awareness of conventional GP. In particular, we propose a ``neural operator-embedded kernel'' wherein the GP kernel is formulated in the latent space learned using a neural operator. Further, we exploit a stochastic dual descent (SDD) algorithm for simultaneously training the neural operator parameters and the GP hyperparameters. Our approach addresses the (a) resolution dependence and (b) cubic complexity of traditional GP models, allowing for input-resolution independence and scalability in high-dimensional and non-linear parametric systems, such as those encountered in computational mechanics. We apply our method to a range of non-linear parametric partial differential equations (PDEs) and demonstrate its superiority in both computational efficiency and accuracy compared to standard GP models and wavelet neural operators. Our experimental results highlight the efficacy of this framework in solving complex PDEs while maintaining robustness in uncertainty estimation, positioning it as a scalable and reliable operator-learning algorithm for computational mechanics.

Alpha-VI DeepONet: A prior-robust variational Bayesian approach for enhancing DeepONets with uncertainty quantification

We introduce a novel deep operator network (DeepONet) framework that incorporates generalised variational inference (GVI) using R\'enyi's $\alpha$-divergence to learn complex operators while quantifying uncertainty. By incorporating Bayesian neural networks as the building blocks for the branch and trunk networks, our framework endows DeepONet with uncertainty quantification. The use of R\'enyi's $\alpha$-divergence, instead of the Kullback-Leibler divergence (KLD), commonly used in standard variational inference, mitigates issues related to prior misspecification that are prevalent in Variational Bayesian DeepONets. This approach offers enhanced flexibility and robustness. We demonstrate that modifying the variational objective function yields superior results in terms of minimising the mean squared error and improving the negative log-likelihood on the test set. Our framework's efficacy is validated across various mechanical systems, where it outperforms both deterministic and standard KLD-based VI DeepONets in predictive accuracy and uncertainty quantification. The hyperparameter $\alpha$, which controls the degree of robustness, can be tuned to optimise performance for specific problems. We apply this approach to a range of mechanics problems, including gravity pendulum, advection-diffusion, and diffusion-reaction systems. Our findings underscore the potential of $\alpha$-VI DeepONet to advance the field of data-driven operator learning and its applications in engineering and scientific domains.

Neural Operator induced Gaussian Process framework for probabilistic solution of parametric partial differential equations

The study of neural operators has paved the way for the development of efficient approaches for solving partial differential equations (PDEs) compared with traditional methods. However, most of the existing neural operators lack the capability to provide uncertainty measures for their predictions, a crucial aspect, especially in data-driven scenarios with limited available data. In this work, we propose a novel Neural Operator-induced Gaussian Process (NOGaP), which exploits the probabilistic characteristics of Gaussian Processes (GPs) while leveraging the learning prowess of operator learning. The proposed framework leads to improved prediction accuracy and offers a quantifiable measure of uncertainty. The proposed framework is extensively evaluated through experiments on various PDE examples, including Burger's equation, Darcy flow, non-homogeneous Poisson, and wave-advection equations. Furthermore, a comparative study with state-of-the-art operator learning algorithms is presented to highlight the advantages of NOGaP. The results demonstrate superior accuracy and expected uncertainty characteristics, suggesting the promising potential of the proposed framework.

Discovering stochastic partial differential equations from limited data using variational Bayes inference

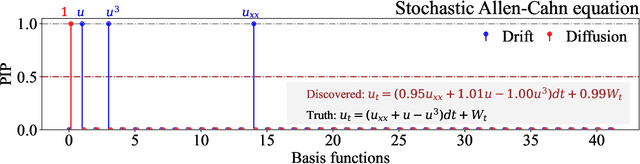
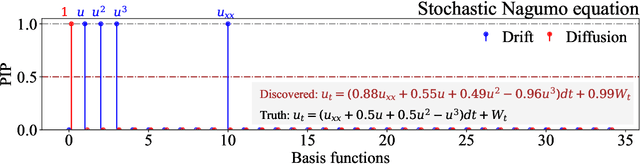
We propose a novel framework for discovering Stochastic Partial Differential Equations (SPDEs) from data. The proposed approach combines the concepts of stochastic calculus, variational Bayes theory, and sparse learning. We propose the extended Kramers-Moyal expansion to express the drift and diffusion terms of an SPDE in terms of state responses and use Spike-and-Slab priors with sparse learning techniques to efficiently and accurately discover the underlying SPDEs. The proposed approach has been applied to three canonical SPDEs, (a) stochastic heat equation, (b) stochastic Allen-Cahn equation, and (c) stochastic Nagumo equation. Our results demonstrate that the proposed approach can accurately identify the underlying SPDEs with limited data. This is the first attempt at discovering SPDEs from data, and it has significant implications for various scientific applications, such as climate modeling, financial forecasting, and chemical kinetics.

A Bayesian Framework for learning governing Partial Differential Equation from Data

The discovery of partial differential equations (PDEs) is a challenging task that involves both theoretical and empirical methods. Machine learning approaches have been developed and used to solve this problem; however, it is important to note that existing methods often struggle to identify the underlying equation accurately in the presence of noise. In this study, we present a new approach to discovering PDEs by combining variational Bayes and sparse linear regression. The problem of PDE discovery has been posed as a problem to learn relevant basis from a predefined dictionary of basis functions. To accelerate the overall process, a variational Bayes-based approach for discovering partial differential equations is proposed. To ensure sparsity, we employ a spike and slab prior. We illustrate the efficacy of our strategy in several examples, including Burgers, Korteweg-de Vries, Kuramoto Sivashinsky, wave equation, and heat equation (1D as well as 2D). Our method offers a promising avenue for discovering PDEs from data and has potential applications in fields such as physics, engineering, and biology.

MAntRA: A framework for model agnostic reliability analysis

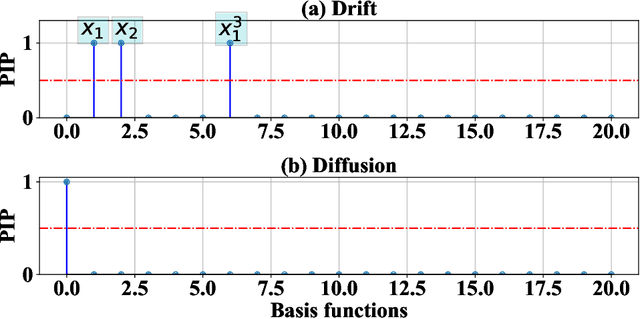
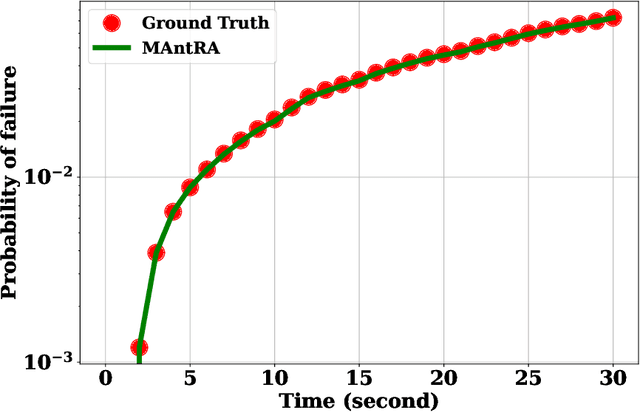
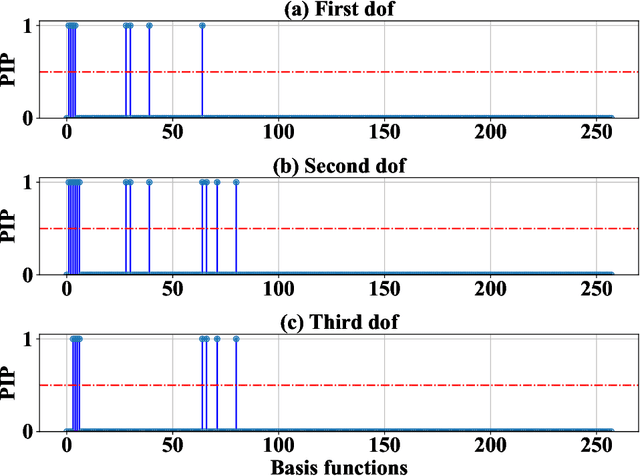
We propose a novel model agnostic data-driven reliability analysis framework for time-dependent reliability analysis. The proposed approach -- referred to as MAntRA -- combines interpretable machine learning, Bayesian statistics, and identifying stochastic dynamic equation to evaluate reliability of stochastically-excited dynamical systems for which the governing physics is \textit{apriori} unknown. A two-stage approach is adopted: in the first stage, an efficient variational Bayesian equation discovery algorithm is developed to determine the governing physics of an underlying stochastic differential equation (SDE) from measured output data. The developed algorithm is efficient and accounts for epistemic uncertainty due to limited and noisy data, and aleatoric uncertainty because of environmental effect and external excitation. In the second stage, the discovered SDE is solved using a stochastic integration scheme and the probability failure is computed. The efficacy of the proposed approach is illustrated on three numerical examples. The results obtained indicate the possible application of the proposed approach for reliability analysis of in-situ and heritage structures from on-site measurements.

A Gaussian process latent force model for joint input-state estimation in linear structural systems

The problem of combined state and input estimation of linear structural systems based on measured responses and a priori knowledge of structural model is considered. A novel methodology using Gaussian process latent force models is proposed to tackle the problem in a stochastic setting. Gaussian process latent force models (GPLFMs) are hybrid models that combine differential equations representing a physical system with data-driven non-parametric Gaussian process models. In this work, the unknown input forces acting on a structure are modelled as Gaussian processes with some chosen covariance functions which are combined with the mechanistic differential equation representing the structure to construct a GPLFM. The GPLFM is then conveniently formulated as an augmented stochastic state-space model with additional states representing the latent force components, and the joint input and state inference of the resulting model is implemented using Kalman filter. The augmented state-space model of GPLFM is shown as a generalization of the class of input-augmented state-space models, is proven observable, and is robust compared to conventional augmented formulations in terms of numerical stability. The hyperparameters governing the covariance functions are estimated using maximum likelihood optimization based on the observed data, thus overcoming the need for manual tuning of the hyperparameters by trial-and-error. To assess the performance of the proposed GPLFM method, several cases of state and input estimation are demonstrated using numerical simulations on a 10-dof shear building and a 76-storey ASCE benchmark office tower. Results obtained indicate the superior performance of the proposed approach over conventional Kalman filter based approaches.