Generative flow induced neural architecture search: Towards discovering optimal architecture in wavelet neural operator

We propose a generative flow-induced neural architecture search algorithm. The proposed approach devices simple feed-forward neural networks to learn stochastic policies to generate sequences of architecture hyperparameters such that the generated states are in proportion with the reward from the terminal state. We demonstrate the efficacy of the proposed search algorithm on the wavelet neural operator (WNO), where we learn a policy to generate a sequence of hyperparameters like wavelet basis and activation operators for wavelet integral blocks. While the trajectory of the generated wavelet basis and activation sequence is cast as flow, the policy is learned by minimizing the flow violation between each state in the trajectory and maximizing the reward from the terminal state. In the terminal state, we train WNO simultaneously to guide the search. We propose to use the exponent of the negative of the WNO loss on the validation dataset as the reward function. While the grid search-based neural architecture generation algorithms foresee every combination, the proposed framework generates the most probable sequence based on the positive reward from the terminal state, thereby reducing exploration time. Compared to reinforcement learning schemes, where complete episodic training is required to get the reward, the proposed algorithm generates the hyperparameter trajectory sequentially. Through four fluid mechanics-oriented problems, we illustrate that the learned policies can sample the best-performing architecture of the neural operator, thereby improving the performance of the vanilla wavelet neural operator.

Generative adversarial wavelet neural operator: Application to fault detection and isolation of multivariate time series data

Fault detection and isolation in complex systems are critical to ensure reliable and efficient operation. However, traditional fault detection methods often struggle with issues such as nonlinearity and multivariate characteristics of the time series variables. This article proposes a generative adversarial wavelet neural operator (GAWNO) as a novel unsupervised deep learning approach for fault detection and isolation of multivariate time series processes.The GAWNO combines the strengths of wavelet neural operators and generative adversarial networks (GANs) to effectively capture both the temporal distributions and the spatial dependencies among different variables of an underlying system. The approach of fault detection and isolation using GAWNO consists of two main stages. In the first stage, the GAWNO is trained on a dataset of normal operating conditions to learn the underlying data distribution. In the second stage, a reconstruction error-based threshold approach using the trained GAWNO is employed to detect and isolate faults based on the discrepancy values. We validate the proposed approach using the Tennessee Eastman Process (TEP) dataset and Avedore wastewater treatment plant (WWTP) and N2O emissions named as WWTPN2O datasets. Overall, we showcase that the idea of harnessing the power of wavelet analysis, neural operators, and generative models in a single framework to detect and isolate faults has shown promising results compared to various well-established baselines in the literature.

A foundational neural operator that continuously learns without forgetting

Machine learning has witnessed substantial growth, leading to the development of advanced artificial intelligence models crafted to address a wide range of real-world challenges spanning various domains, such as computer vision, natural language processing, and scientific computing. Nevertheless, the creation of custom models for each new task remains a resource-intensive undertaking, demanding considerable computational time and memory resources. In this study, we introduce the concept of the Neural Combinatorial Wavelet Neural Operator (NCWNO) as a foundational model for scientific computing. This model is specifically designed to excel in learning from a diverse spectrum of physics and continuously adapt to the solution operators associated with parametric partial differential equations (PDEs). The NCWNO leverages a gated structure that employs local wavelet experts to acquire shared features across multiple physical systems, complemented by a memory-based ensembling approach among these local wavelet experts. This combination enables rapid adaptation to new challenges. The proposed foundational model offers two key advantages: (i) it can simultaneously learn solution operators for multiple parametric PDEs, and (ii) it can swiftly generalize to new parametric PDEs with minimal fine-tuning. The proposed NCWNO is the first foundational operator learning algorithm distinguished by its (i) robustness against catastrophic forgetting, (ii) the maintenance of positive transfer for new parametric PDEs, and (iii) the facilitation of knowledge transfer across dissimilar tasks. Through an extensive set of benchmark examples, we demonstrate that the NCWNO can outperform task-specific baseline operator learning frameworks with minimal hyperparameter tuning at the prediction stage. We also show that with minimal fine-tuning, the NCWNO performs accurate combinatorial learning of new parametric PDEs.

A Bayesian framework for discovering interpretable Lagrangian of dynamical systems from data

Learning and predicting the dynamics of physical systems requires a profound understanding of the underlying physical laws. Recent works on learning physical laws involve generalizing the equation discovery frameworks to the discovery of Hamiltonian and Lagrangian of physical systems. While the existing methods parameterize the Lagrangian using neural networks, we propose an alternate framework for learning interpretable Lagrangian descriptions of physical systems from limited data using the sparse Bayesian approach. Unlike existing neural network-based approaches, the proposed approach (a) yields an interpretable description of Lagrangian, (b) exploits Bayesian learning to quantify the epistemic uncertainty due to limited data, (c) automates the distillation of Hamiltonian from the learned Lagrangian using Legendre transformation, and (d) provides ordinary (ODE) and partial differential equation (PDE) based descriptions of the observed systems. Six different examples involving both discrete and continuous system illustrates the efficacy of the proposed approach.

Discovering stochastic partial differential equations from limited data using variational Bayes inference

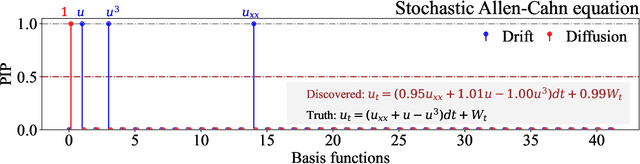
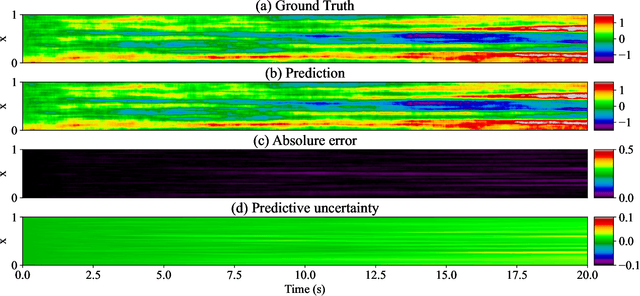
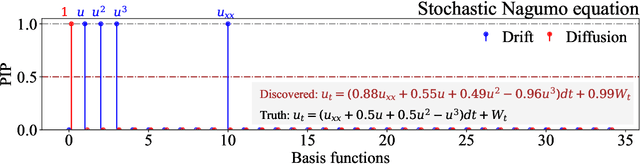
We propose a novel framework for discovering Stochastic Partial Differential Equations (SPDEs) from data. The proposed approach combines the concepts of stochastic calculus, variational Bayes theory, and sparse learning. We propose the extended Kramers-Moyal expansion to express the drift and diffusion terms of an SPDE in terms of state responses and use Spike-and-Slab priors with sparse learning techniques to efficiently and accurately discover the underlying SPDEs. The proposed approach has been applied to three canonical SPDEs, (a) stochastic heat equation, (b) stochastic Allen-Cahn equation, and (c) stochastic Nagumo equation. Our results demonstrate that the proposed approach can accurately identify the underlying SPDEs with limited data. This is the first attempt at discovering SPDEs from data, and it has significant implications for various scientific applications, such as climate modeling, financial forecasting, and chemical kinetics.

A Bayesian Framework for learning governing Partial Differential Equation from Data

The discovery of partial differential equations (PDEs) is a challenging task that involves both theoretical and empirical methods. Machine learning approaches have been developed and used to solve this problem; however, it is important to note that existing methods often struggle to identify the underlying equation accurately in the presence of noise. In this study, we present a new approach to discovering PDEs by combining variational Bayes and sparse linear regression. The problem of PDE discovery has been posed as a problem to learn relevant basis from a predefined dictionary of basis functions. To accelerate the overall process, a variational Bayes-based approach for discovering partial differential equations is proposed. To ensure sparsity, we employ a spike and slab prior. We illustrate the efficacy of our strategy in several examples, including Burgers, Korteweg-de Vries, Kuramoto Sivashinsky, wave equation, and heat equation (1D as well as 2D). Our method offers a promising avenue for discovering PDEs from data and has potential applications in fields such as physics, engineering, and biology.

Physics informed WNO

Deep neural operators are recognized as an effective tool for learning solution operators of complex partial differential equations (PDEs). As compared to laborious analytical and computational tools, a single neural operator can predict solutions of PDEs for varying initial or boundary conditions and different inputs. A recently proposed Wavelet Neural Operator (WNO) is one such operator that harnesses the advantage of time-frequency localization of wavelets to capture the manifolds in the spatial domain effectively. While WNO has proven to be a promising method for operator learning, the data-hungry nature of the framework is a major shortcoming. In this work, we propose a physics-informed WNO for learning the solution operators of families of parametric PDEs without labeled training data. The efficacy of the framework is validated and illustrated with four nonlinear spatiotemporal systems relevant to various fields of engineering and science.

Discovering interpretable Lagrangian of dynamical systems from data

A complete understanding of physical systems requires models that are accurate and obeys natural conservation laws. Recent trends in representation learning involve learning Lagrangian from data rather than the direct discovery of governing equations of motion. The generalization of equation discovery techniques has huge potential; however, existing Lagrangian discovery frameworks are black-box in nature. This raises a concern about the reusability of the discovered Lagrangian. In this article, we propose a novel data-driven machine-learning algorithm to automate the discovery of interpretable Lagrangian from data. The Lagrangian are derived in interpretable forms, which also allows the automated discovery of conservation laws and governing equations of motion. The architecture of the proposed framework is designed in such a way that it allows learning the Lagrangian from a subset of the underlying domain and then generalizing for an infinite-dimensional system. The fidelity of the proposed framework is exemplified using examples described by systems of ordinary differential equations and partial differential equations where the Lagrangian and conserved quantities are known.

Probabilistic machine learning based predictive and interpretable digital twin for dynamical systems

A framework for creating and updating digital twins for dynamical systems from a library of physics-based functions is proposed. The sparse Bayesian machine learning is used to update and derive an interpretable expression for the digital twin. Two approaches for updating the digital twin are proposed. The first approach makes use of both the input and output information from a dynamical system, whereas the second approach utilizes output-only observations to update the digital twin. Both methods use a library of candidate functions representing certain physics to infer new perturbation terms in the existing digital twin model. In both cases, the resulting expressions of updated digital twins are identical, and in addition, the epistemic uncertainties are quantified. In the first approach, the regression problem is derived from a state-space model, whereas in the latter case, the output-only information is treated as a stochastic process. The concepts of It\^o calculus and Kramers-Moyal expansion are being utilized to derive the regression equation. The performance of the proposed approaches is demonstrated using highly nonlinear dynamical systems such as the crack-degradation problem. Numerical results demonstrated in this paper almost exactly identify the correct perturbation terms along with their associated parameters in the dynamical system. The probabilistic nature of the proposed approach also helps in quantifying the uncertainties associated with updated models. The proposed approaches provide an exact and explainable description of the perturbations in digital twin models, which can be directly used for better cyber-physical integration, long-term future predictions, degradation monitoring, and model-agnostic control.

MAntRA: A framework for model agnostic reliability analysis

We propose a novel model agnostic data-driven reliability analysis framework for time-dependent reliability analysis. The proposed approach -- referred to as MAntRA -- combines interpretable machine learning, Bayesian statistics, and identifying stochastic dynamic equation to evaluate reliability of stochastically-excited dynamical systems for which the governing physics is \textit{apriori} unknown. A two-stage approach is adopted: in the first stage, an efficient variational Bayesian equation discovery algorithm is developed to determine the governing physics of an underlying stochastic differential equation (SDE) from measured output data. The developed algorithm is efficient and accounts for epistemic uncertainty due to limited and noisy data, and aleatoric uncertainty because of environmental effect and external excitation. In the second stage, the discovered SDE is solved using a stochastic integration scheme and the probability failure is computed. The efficacy of the proposed approach is illustrated on three numerical examples. The results obtained indicate the possible application of the proposed approach for reliability analysis of in-situ and heritage structures from on-site measurements.