CoNBONet: Conformalized Neuroscience-inspired Bayesian Operator Network for Reliability Analysis

Time-dependent reliability analysis of nonlinear dynamical systems under stochastic excitations is a critical yet computationally demanding task. Conventional approaches, such as Monte Carlo simulation, necessitate repeated evaluations of computationally expensive numerical solvers, leading to significant computational bottlenecks. To address this challenge, we propose \textit{CoNBONet}, a neuroscience-inspired surrogate model that enables fast, energy-efficient, and uncertainty-aware reliability analysis, providing a scalable alternative to techniques such as Monte Carlo simulations. CoNBONet, short for \textbf{Co}nformalized \textbf{N}euroscience-inspired \textbf{B}ayesian \textbf{O}perator \textbf{Net}work, leverages the expressive power of deep operator networks while integrating neuroscience-inspired neuron models to achieve fast, low-power inference. Unlike traditional surrogates such as Gaussian processes, polynomial chaos expansions, or support vector regression, that may face scalability challenges for high-dimensional, time-dependent reliability problems, CoNBONet offers \textit{fast and energy-efficient inference} enabled by a neuroscience-inspired network architecture, \textit{calibrated uncertainty quantification with theoretical guarantees} via split conformal prediction, and \textit{strong generalization capability} through an operator-learning paradigm that maps input functions to system response trajectories. Validation of the proposed CoNBONet for various nonlinear dynamical systems demonstrates that CoNBONet preserves predictive fidelity, and achieves reliable coverage of failure probabilities, making it a powerful tool for robust and scalable reliability analysis in engineering design.

Adversarial Vulnerabilities in Neural Operator Digital Twins: Gradient-Free Attacks on Nuclear Thermal-Hydraulic Surrogates

Operator learning models are rapidly emerging as the predictive core of digital twins for nuclear and energy systems, promising real-time field reconstruction from sparse sensor measurements. Yet their robustness to adversarial perturbations remains uncharacterized, a critical gap for deployment in safety-critical systems. Here we show that neural operators are acutely vulnerable to extremely sparse (fewer than 1% of inputs), physically plausible perturbations that exploit their sensitivity to boundary conditions. Using gradient-free differential evolution across four operator architectures, we demonstrate that minimal modifications trigger catastrophic prediction failures, increasing relative $L_2$ error from $\sim$1.5% (validated accuracy) to 37-63% while remaining completely undetectable by standard validation metrics. Notably, 100% of successful single-point attacks pass z-score anomaly detection. We introduce the effective perturbation dimension $d_{\text{eff}}$, a Jacobian-based diagnostic that, together with sensitivity magnitude, yields a two-factor vulnerability model explaining why architectures with extreme sensitivity concentration (POD-DeepONet, $d_{\text{eff}} \approx 1$) are not necessarily the most exploitable, since low-rank output projections cap maximum error, while moderate concentration with sufficient amplification (S-DeepONet, $d_{\text{eff}} \approx 4$) produces the highest attack success. Gradient-free search outperforms gradient-based alternatives (PGD) on architectures with gradient pathologies, while random perturbations of equal magnitude achieve near-zero success rates, confirming that the discovered vulnerabilities are structural. Our findings expose a previously overlooked attack surface in operator learning models and establish that these models require robustness guarantees beyond standard validation before deployment.

SPINONet: Scalable Spiking Physics-informed Neural Operator for Computational Mechanics Applications

Energy efficiency remains a critical challenge in deploying physics-informed operator learning models for computational mechanics and scientific computing, particularly in power-constrained settings such as edge and embedded devices, where repeated operator evaluations in dense networks incur substantial computational and energy costs. To address this challenge, we introduce the Separable Physics-informed Neuroscience-inspired Operator Network (SPINONet), a neuroscience-inspired framework that reduces redundant computation across repeated evaluations while remaining compatible with physics-informed training. SPINONet incorporates regression-friendly neuroscience-inspired spiking neurons through an architecture-aware design that enables sparse, event-driven computation, improving energy efficiency while preserving the continuous, coordinate-differentiable pathways required for computing spatio-temporal derivatives. We evaluate SPINONet on a range of partial differential equations representative of computational mechanics problems, with spatial, temporal, and parametric dependencies in both time-dependent and steady-state settings, and demonstrate predictive performance comparable to conventional physics-informed operator learning approaches despite the induced sparse communication. In addition, limited data supervision in a hybrid setup is shown to improve performance in challenging regimes where purely physics-informed training may converge to spurious solutions. Finally, we provide an analytical discussion linking architectural components and design choices of SPINONet to reductions in computational load and energy consumption.

TrustFed: Enabling Trustworthy Medical AI under Data Privacy Constraints

Protecting patient privacy remains a fundamental barrier to scaling machine learning across healthcare institutions, where centralizing sensitive data is often infeasible due to ethical, legal, and regulatory constraints. Federated learning offers a promising alternative by enabling privacy-preserving, multi-institutional training without sharing raw patient data; however, real-world deployments face severe challenges from data heterogeneity, site-specific biases, and class imbalance, which degrade predictive reliability and render existing uncertainty quantification methods ineffective. Here, we present TrustFed, a federated uncertainty quantification framework that provides distribution-free, finite-sample coverage guarantees under heterogeneous and imbalanced healthcare data, without requiring centralized access. TrustFed introduces a representation-aware client assignment mechanism that leverages internal model representations to enable effective calibration across institutions, along with a soft-nearest threshold aggregation strategy that mitigates assignment uncertainty while producing compact and reliable prediction sets. Using over 430,000 medical images across six clinically distinct imaging modalities, we conduct one of the most comprehensive evaluations of uncertainty-aware federated learning in medical imaging, demonstrating robust coverage guarantees across datasets with diverse class cardinalities and imbalance regimes. By validating TrustFed at this scale and breadth, our study advances uncertainty-aware federated learning from proof-of-concept toward clinically meaningful, modality-agnostic deployment, positioning statistically guaranteed uncertainty as a core requirement for next-generation healthcare AI systems.

Scalable Random Wavelet Features: Efficient Non-Stationary Kernel Approximation with Convergence Guarantees

Modeling non-stationary processes, where statistical properties vary across the input domain, is a critical challenge in machine learning; yet most scalable methods rely on a simplifying assumption of stationarity. This forces a difficult trade-off: use expressive but computationally demanding models like Deep Gaussian Processes, or scalable but limited methods like Random Fourier Features (RFF). We close this gap by introducing Random Wavelet Features (RWF), a framework that constructs scalable, non-stationary kernel approximations by sampling from wavelet families. By harnessing the inherent localization and multi-resolution structure of wavelets, RWF generates an explicit feature map that captures complex, input-dependent patterns. Our framework provides a principled way to generalize RFF to the non-stationary setting and comes with a comprehensive theoretical analysis, including positive definiteness, unbiasedness, and uniform convergence guarantees. We demonstrate empirically on a range of challenging synthetic and real-world datasets that RWF outperforms stationary random features and offers a compelling accuracy-efficiency trade-off against more complex models, unlocking scalable and expressive kernel methods for a broad class of real-world non-stationary problems.

CortiNet: A Physics-Perception Hybrid Cortical-Inspired Dual-Stream Network for Gallbladder Disease Diagnosis from Ultrasound

Ultrasound imaging is the primary diagnostic modality for detecting Gallbladder diseases due to its non-invasive nature, affordability, and wide accessibility. However, the low resolution and speckle noise inherent to ultrasound images hinder diagnostic reliability, prompting the use of large convolutional neural networks that are difficult to deploy in routine clinical settings. In this work, we propose CortiNet, a lightweight, cortical-inspired dual-stream neural architecture for gallbladder disease diagnosis that integrates physically interpretable multi-scale signal decomposition with perception-driven feature learning. Inspired by parallel processing pathways in the human visual cortex, CortiNet explicitly separates low-frequency structural information from high-frequency perceptual details and processes them through specialized encoding streams. By operating directly on structured, frequency-selective representations rather than raw pixel intensities, the architecture embeds strong physics-based inductive bias, enabling efficient feature learning with a significantly reduced parameter footprint. A late-stage cortical-style fusion mechanism integrates complementary structural and textural cues while preserving computational efficiency. Additionally, we propose a structure-aware explainability framework wherein gradient-weighted class activation mapping is only applied to the structural branch of the proposed CortiNet architecture. This choice allows the model to only focus on the structural features, making it robust against speckle noise. We evaluate CortiNet on 10,692 expert-annotated images spanning nine clinically relevant gallbladder disease categories. Experimental results demonstrate that CortiNet achieves high diagnostic accuracy (98.74%) with only a fraction of the parameters required by conventional deep convolutional models.

Agentic Physical AI toward a Domain-Specific Foundation Model for Nuclear Reactor Control

The prevailing paradigm in AI for physical systems, scaling general-purpose foundation models toward universal multimodal reasoning, confronts a fundamental barrier at the control interface. Recent benchmarks show that even frontier vision-language models achieve only 50-53% accuracy on basic quantitative physics tasks, behaving as approximate guessers that preserve semantic plausibility while violating physical constraints. This input unfaithfulness is not a scaling deficiency but a structural limitation. Perception-centric architectures optimize parameter-space imitation, whereas safety-critical control demands outcome-space guarantees over executed actions. Here, we present a fundamentally different pathway toward domain-specific foundation models by introducing compact language models operating as Agentic Physical AI, in which policy optimization is driven by physics-based validation rather than perceptual inference. We train a 360-million-parameter model on synthetic reactor control scenarios, scaling the dataset from 10^3 to 10^5 examples. This induces a sharp phase transition absent in general-purpose models. Small-scale systems exhibit high-variance imitation with catastrophic tail risk, while large-scale models undergo variance collapse exceeding 500x reduction, stabilizing execution-level behavior. Despite balanced exposure to four actuation families, the model autonomously rejects approximately 70% of the training distribution and concentrates 95% of runtime execution on a single-bank strategy. Learned representations transfer across distinct physics and continuous input modalities without architectural modification.

Event-driven physics-informed operator learning for reliability analysis

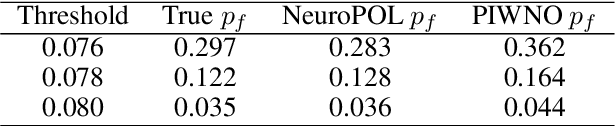
Reliability analysis of engineering systems under uncertainty poses significant computational challenges, particularly for problems involving high-dimensional stochastic inputs, nonlinear system responses, and multiphysics couplings. Traditional surrogate modeling approaches often incur high energy consumption, which severely limits their scalability and deployability in resource-constrained environments. We introduce NeuroPOL, \textit{the first neuroscience-inspired physics-informed operator learning framework} for reliability analysis. NeuroPOL incorporates Variable Spiking Neurons into a physics-informed operator architecture, replacing continuous activations with event-driven spiking dynamics. This innovation promotes sparse communication, significantly reduces computational load, and enables an energy-efficient surrogate model. The proposed framework lowers both computational and power demands, supporting real-time reliability assessment and deployment on edge devices and digital twins. By embedding governing physical laws into operator learning, NeuroPOL builds physics-consistent surrogates capable of accurate uncertainty propagation and efficient failure probability estimation, even for high-dimensional problems. We evaluate NeuroPOL on five canonical benchmarks, the Burgers equation, Nagumo equation, two-dimensional Poisson equation, two-dimensional Darcy equation, and incompressible Navier-Stokes equation with energy coupling. Results show that NeuroPOL achieves reliability measures comparable to standard physics-informed operators, while introducing significant communication sparsity, enabling scalable, distributed, and energy-efficient deployment.

Deep Muscle EMG construction using A Physics-Integrated Deep Learning approach

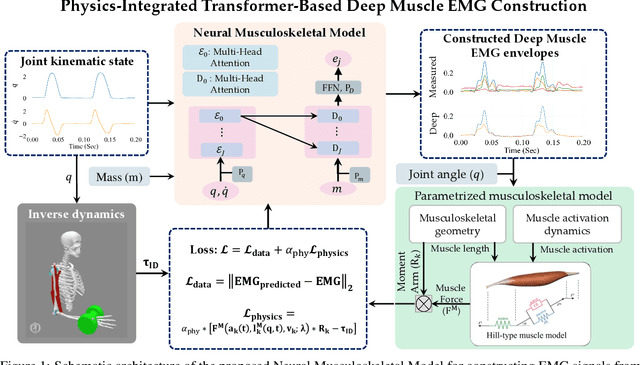
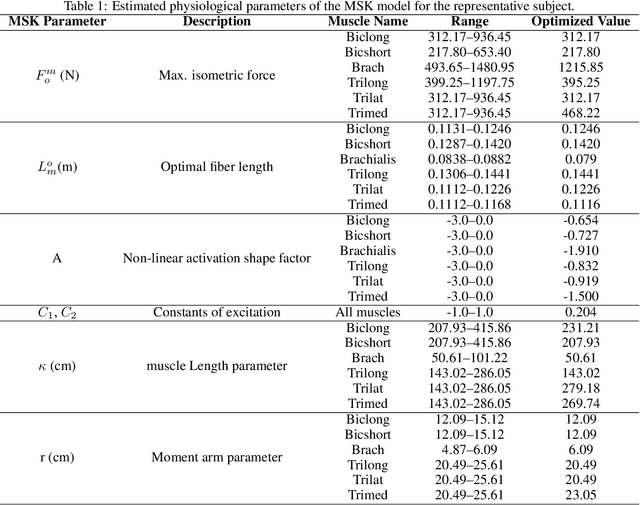
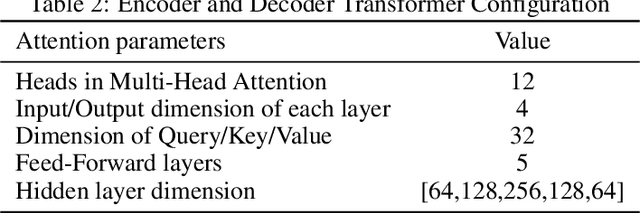
Electromyography (EMG)--based computational musculoskeletal modeling is a non-invasive method for studying musculotendon function, human movement, and neuromuscular control, providing estimates of internal variables like muscle forces and joint torques. However, EMG signals from deeper muscles are often challenging to measure by placing the surface EMG electrodes and unfeasible to measure directly using invasive methods. The restriction to the access of EMG data from deeper muscles poses a considerable obstacle to the broad adoption of EMG-driven modeling techniques. A strategic alternative is to use an estimation algorithm to approximate the missing EMG signals from deeper muscle. A similar strategy is used in physics-informed deep learning, where the features of physical systems are learned without labeled data. In this work, we propose a hybrid deep learning algorithm, namely the neural musculoskeletal model (NMM), that integrates physics-informed and data-driven deep learning to approximate the EMG signals from the deeper muscles. While data-driven modeling is used to predict the missing EMG signals, physics-based modeling engraves the subject-specific information into the predictions. Experimental verifications on five test subjects are carried out to investigate the performance of the proposed hybrid framework. The proposed NMM is validated against the joint torque computed from 'OpenSim' software. The predicted deep EMG signals are also compared against the state-of-the-art muscle synergy extrapolation (MSE) approach, where the proposed NMM completely outperforms the existing MSE framework by a significant margin.

A Bayesian Approach for Discovering Time- Delayed Differential Equation from Data

Time-delayed differential equations (TDDEs) are widely used to model complex dynamic systems where future states depend on past states with a delay. However, inferring the underlying TDDEs from observed data remains a challenging problem due to the inherent nonlinearity, uncertainty, and noise in real-world systems. Conventional equation discovery methods often exhibit limitations when dealing with large time delays, relying on deterministic techniques or optimization-based approaches that may struggle with scalability and robustness. In this paper, we present BayTiDe - Bayesian Approach for Discovering Time-Delayed Differential Equations from Data, that is capable of identifying arbitrarily large values of time delay to an accuracy that is directly proportional to the resolution of the data input to it. BayTiDe leverages Bayesian inference combined with a sparsity-promoting discontinuous spike-and-slab prior to accurately identify time-delayed differential equations. The approach accommodates arbitrarily large time delays with accuracy proportional to the input data resolution, while efficiently narrowing the search space to achieve significant computational savings. We demonstrate the efficiency and robustness of BayTiDe through a range of numerical examples, validating its ability to recover delayed differential equations from noisy data.