Hybrid variable spiking graph neural networks for energy-efficient scientific machine learning

Graph-based representations for samples of computational mechanics-related datasets can prove instrumental when dealing with problems like irregular domains or molecular structures of materials, etc. To effectively analyze and process such datasets, deep learning offers Graph Neural Networks (GNNs) that utilize techniques like message-passing within their architecture. The issue, however, is that as the individual graph scales and/ or GNN architecture becomes increasingly complex, the increased energy budget of the overall deep learning model makes it unsustainable and restricts its applications in applications like edge computing. To overcome this, we propose in this paper Hybrid Variable Spiking Graph Neural Networks (HVS-GNNs) that utilize Variable Spiking Neurons (VSNs) within their architecture to promote sparse communication and hence reduce the overall energy budget. VSNs, while promoting sparse event-driven computations, also perform well for regression tasks, which are often encountered in computational mechanics applications and are the main target of this paper. Three examples dealing with prediction of mechanical properties of material based on microscale/ mesoscale structures are shown to test the performance of the proposed HVS-GNNs in regression tasks. We have also compared the performance of HVS-GNN architectures with the performance of vanilla GNNs and GNNs utilizing leaky integrate and fire neurons. The results produced show that HVS-GNNs perform well for regression tasks, all while promoting sparse communication and, hence, energy efficiency.

Neuroscience inspired scientific machine learning : Variable spiking wavelet neural operator

We propose, in this paper, a Variable Spiking Wavelet Neural Operator (VS-WNO), which aims to bridge the gap between theoretical and practical implementation of Artificial Intelligence (AI) algorithms for mechanics applications. With recent developments like the introduction of neural operators, AI's potential for being used in mechanics applications has increased significantly. However, AI's immense energy and resource requirements are a hurdle in its practical field use case. The proposed VS-WNO is based on the principles of spiking neural networks, which have shown promise in reducing the energy requirements of the neural networks. This makes possible the use of such algorithms in edge computing. The proposed VS-WNO utilizes variable spiking neurons, which promote sparse communication, thus conserving energy, and its use is further supported by its ability to tackle regression tasks, often faced in the field of mechanics. Various examples dealing with partial differential equations, like Burger's equation, Allen Cahn's equation, and Darcy's equation, have been shown. Comparisons have been shown against wavelet neural operator utilizing leaky integrate and fire neurons (direct and encoded inputs) and vanilla wavelet neural operator utilizing artificial neurons. The results produced illustrate the ability of the proposed VS-WNO to converge to ground truth while promoting sparse communication.

Neuroscience inspired scientific machine learning (Part-1): Variable spiking neuron for regression

Redundant information transfer in a neural network can increase the complexity of the deep learning model, thus increasing its power consumption. We introduce in this paper a novel spiking neuron, termed Variable Spiking Neuron (VSN), which can reduce the redundant firing using lessons from biological neuron inspired Leaky Integrate and Fire Spiking Neurons (LIF-SN). The proposed VSN blends LIF-SN and artificial neurons. It garners the advantage of intermittent firing from the LIF-SN and utilizes the advantage of continuous activation from the artificial neuron. This property of the proposed VSN makes it suitable for regression tasks, which is a weak point for the vanilla spiking neurons, all while keeping the energy budget low. The proposed VSN is tested against both classification and regression tasks. The results produced advocate favorably towards the efficacy of the proposed spiking neuron, particularly for regression tasks.

Randomized prior wavelet neural operator for uncertainty quantification

In this paper, we propose a novel data-driven operator learning framework referred to as the \textit{Randomized Prior Wavelet Neural Operator} (RP-WNO). The proposed RP-WNO is an extension of the recently proposed wavelet neural operator, which boasts excellent generalizing capabilities but cannot estimate the uncertainty associated with its predictions. RP-WNO, unlike the vanilla WNO, comes with inherent uncertainty quantification module and hence, is expected to be extremely useful for scientists and engineers alike. RP-WNO utilizes randomized prior networks, which can account for prior information and is easier to implement for large, complex deep-learning architectures than its Bayesian counterpart. Four examples have been solved to test the proposed framework, and the results produced advocate favorably for the efficacy of the proposed framework.

Variational Bayes Deep Operator Network: A data-driven Bayesian solver for parametric differential equations

Neural network based data-driven operator learning schemes have shown tremendous potential in computational mechanics. DeepONet is one such neural network architecture which has gained widespread appreciation owing to its excellent prediction capabilities. Having said that, being set in a deterministic framework exposes DeepONet architecture to the risk of overfitting, poor generalization and in its unaltered form, it is incapable of quantifying the uncertainties associated with its predictions. We propose in this paper, a Variational Bayes DeepONet (VB-DeepONet) for operator learning, which can alleviate these limitations of DeepONet architecture to a great extent and give user additional information regarding the associated uncertainty at the prediction stage. The key idea behind neural networks set in Bayesian framework is that, the weights and bias of the neural network are treated as probability distributions instead of point estimates and, Bayesian inference is used to update their prior distribution. Now, to manage the computational cost associated with approximating the posterior distribution, the proposed VB-DeepONet uses \textit{variational inference}. Unlike Markov Chain Monte Carlo schemes, variational inference has the capacity to take into account high dimensional posterior distributions while keeping the associated computational cost low. Different examples covering mechanics problems like diffusion reaction, gravity pendulum, advection diffusion have been shown to illustrate the performance of the proposed VB-DeepONet and comparisons have also been drawn against DeepONet set in deterministic framework.

Assessment of DeepONet for reliability analysis of stochastic nonlinear dynamical systems

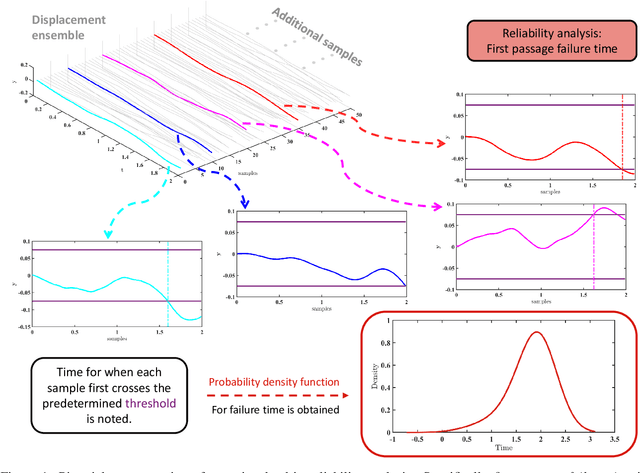
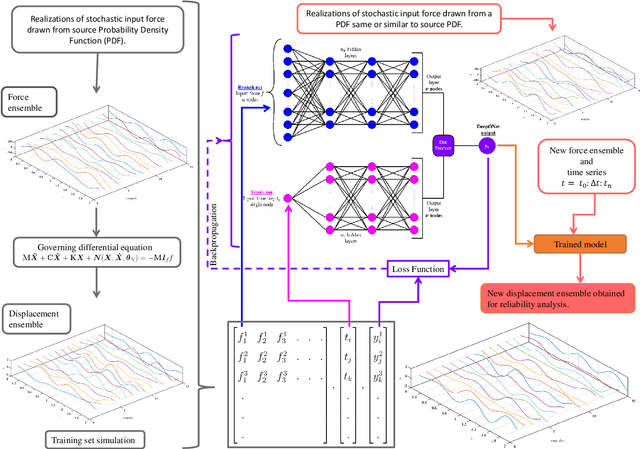
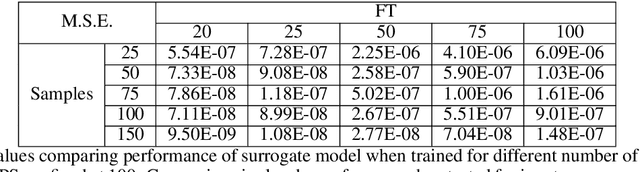
Time dependent reliability analysis and uncertainty quantification of structural system subjected to stochastic forcing function is a challenging endeavour as it necessitates considerable computational time. We investigate the efficacy of recently proposed DeepONet in solving time dependent reliability analysis and uncertainty quantification of systems subjected to stochastic loading. Unlike conventional machine learning and deep learning algorithms, DeepONet learns is a operator network and learns a function to function mapping and hence, is ideally suited to propagate the uncertainty from the stochastic forcing function to the output responses. We use DeepONet to build a surrogate model for the dynamical system under consideration. Multiple case studies, involving both toy and benchmark problems, have been conducted to examine the efficacy of DeepONet in time dependent reliability analysis and uncertainty quantification of linear and nonlinear dynamical systems. Results obtained indicate that the DeepONet architecture is accurate as well as efficient. Moreover, DeepONet posses zero shot learning capabilities and hence, a trained model easily generalizes to unseen and new environment with no further training.

Physics-integrated hybrid framework for model form error identification in nonlinear dynamical systems

For real-life nonlinear systems, the exact form of nonlinearity is often not known and the known governing equations are often based on certain assumptions and approximations. Such representation introduced model-form error into the system. In this paper, we propose a novel gray-box modeling approach that not only identifies the model-form error but also utilizes it to improve the predictive capability of the known but approximate governing equation. The primary idea is to treat the unknown model-form error as a residual force and estimate it using duel Bayesian filter based joint input-state estimation algorithms. For improving the predictive capability of the underlying physics, we first use machine learning algorithm to learn a mapping between the estimated state and the input (model-form error) and then introduce it into the governing equation as an additional term. This helps in improving the predictive capability of the governing physics and allows the model to generalize to unseen environment. Although in theory, any machine learning algorithm can be used within the proposed framework, we use Gaussian process in this work. To test the performance of proposed framework, case studies discussing four different dynamical systems are discussed; results for which indicate that the framework is applicable to a wide variety of systems and can produce reliable estimates of original system's states.

Machine learning based digital twin for stochastic nonlinear multi-degree of freedom dynamical system

The potential of digital twin technology is immense, specifically in the infrastructure, aerospace, and automotive sector. However, practical implementation of this technology is not at an expected speed, specifically because of lack of application-specific details. In this paper, we propose a novel digital twin framework for stochastic nonlinear multi-degree of freedom (MDOF) dynamical systems. The approach proposed in this paper strategically decouples the problem into two time-scales -- (a) a fast time-scale governing the system dynamics and (b) a slow time-scale governing the degradation in the system. The proposed digital twin has four components - (a) a physics-based nominal model (low-fidelity), (b) a Bayesian filtering algorithm a (c) a supervised machine learning algorithm and (d) a high-fidelity model for predicting future responses. The physics-based nominal model combined with Bayesian filtering is used combined parameter state estimation and the supervised machine learning algorithm is used for learning the temporal evolution of the parameters. While the proposed framework can be used with any choice of Bayesian filtering and machine learning algorithm, we propose to use unscented Kalman filter and Gaussian process. Performance of the proposed approach is illustrated using two examples. Results obtained indicate the applicability and excellent performance of the proposed digital twin framework.