Probabilistic machine learning based predictive and interpretable digital twin for dynamical systems

A framework for creating and updating digital twins for dynamical systems from a library of physics-based functions is proposed. The sparse Bayesian machine learning is used to update and derive an interpretable expression for the digital twin. Two approaches for updating the digital twin are proposed. The first approach makes use of both the input and output information from a dynamical system, whereas the second approach utilizes output-only observations to update the digital twin. Both methods use a library of candidate functions representing certain physics to infer new perturbation terms in the existing digital twin model. In both cases, the resulting expressions of updated digital twins are identical, and in addition, the epistemic uncertainties are quantified. In the first approach, the regression problem is derived from a state-space model, whereas in the latter case, the output-only information is treated as a stochastic process. The concepts of It\^o calculus and Kramers-Moyal expansion are being utilized to derive the regression equation. The performance of the proposed approaches is demonstrated using highly nonlinear dynamical systems such as the crack-degradation problem. Numerical results demonstrated in this paper almost exactly identify the correct perturbation terms along with their associated parameters in the dynamical system. The probabilistic nature of the proposed approach also helps in quantifying the uncertainties associated with updated models. The proposed approaches provide an exact and explainable description of the perturbations in digital twin models, which can be directly used for better cyber-physical integration, long-term future predictions, degradation monitoring, and model-agnostic control.

Machine learning based digital twin for dynamical systems with multiple time-scales

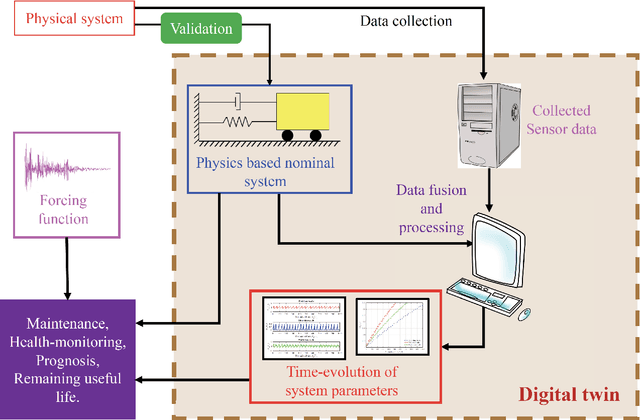
Digital twin technology has a huge potential for widespread applications in different industrial sectors such as infrastructure, aerospace, and automotive. However, practical adoptions of this technology have been slower, mainly due to a lack of application-specific details. Here we focus on a digital twin framework for linear single-degree-of-freedom structural dynamic systems evolving in two different operational time scales in addition to its intrinsic dynamic time-scale. Our approach strategically separates into two components -- (a) a physics-based nominal model for data processing and response predictions, and (b) a data-driven machine learning model for the time-evolution of the system parameters. The physics-based nominal model is system-specific and selected based on the problem under consideration. On the other hand, the data-driven machine learning model is generic. For tracking the multi-scale evolution of the system parameters, we propose to exploit a mixture of experts as the data-driven model. Within the mixture of experts model, Gaussian Process (GP) is used as the expert model. The primary idea is to let each expert track the evolution of the system parameters at a single time-scale. For learning the hyperparameters of the `mixture of experts using GP', an efficient framework the exploits expectation-maximization and sequential Monte Carlo sampler is used. Performance of the digital twin is illustrated on a multi-timescale dynamical system with stiffness and/or mass variations. The digital twin is found to be robust and yields reasonably accurate results. One exciting feature of the proposed digital twin is its capability to provide reasonable predictions at future time-steps. Aspects related to the data quality and data quantity are also investigated.

The role of surrogate models in the development of digital twins of dynamic systems

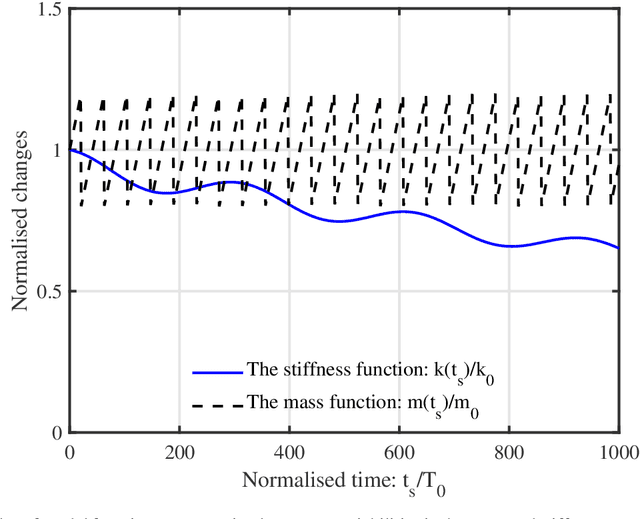
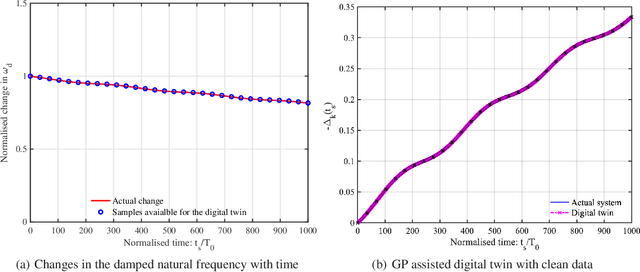
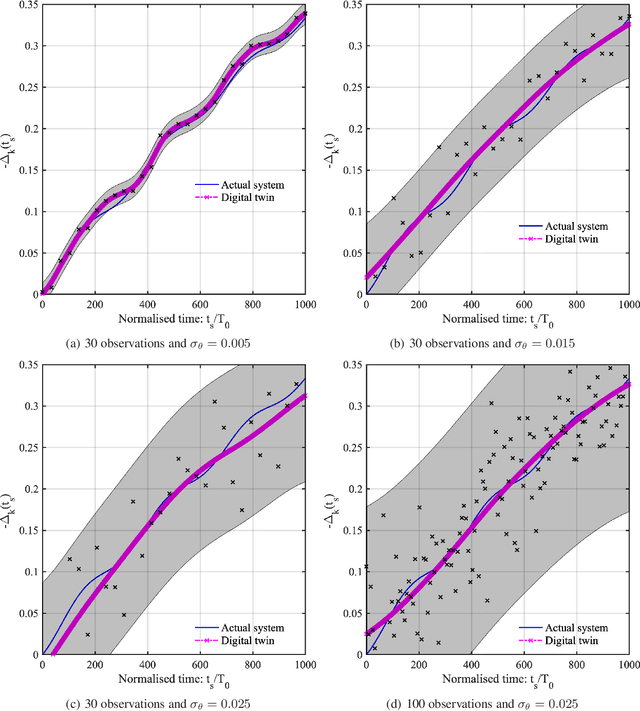
Digital twin technology has significant promise, relevance and potential of widespread applicability in various industrial sectors such as aerospace, infrastructure and automotive. However, the adoption of this technology has been slower due to the lack of clarity for specific applications. A discrete damped dynamic system is used in this paper to explore the concept of a digital twin. As digital twins are also expected to exploit data and computational methods, there is a compelling case for the use of surrogate models in this context. Motivated by this synergy, we have explored the possibility of using surrogate models within the digital twin technology. In particular, the use of Gaussian process (GP) emulator within the digital twin technology is explored. GP has the inherent capability of addressing noise and sparse data and hence, makes a compelling case to be used within the digital twin framework. Cases involving stiffness variation and mass variation are considered, individually and jointly along with different levels of noise and sparsity in data. Our numerical simulation results clearly demonstrate that surrogate models such as GP emulators have the potential to be an effective tool for the development of digital twins. Aspects related to data quality and sampling rate are analysed. Key concepts introduced in this paper are summarised and ideas for urgent future research needs are proposed.

Finite element model selection using Particle Swarm Optimization

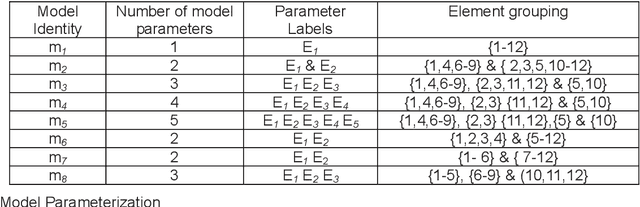
This paper proposes the application of particle swarm optimization (PSO) to the problem of finite element model (FEM) selection. This problem arises when a choice of the best model for a system has to be made from set of competing models, each developed a priori from engineering judgment. PSO is a population-based stochastic search algorithm inspired by the behaviour of biological entities in nature when they are foraging for resources. Each potentially correct model is represented as a particle that exhibits both individualistic and group behaviour. Each particle moves within the model search space looking for the best solution by updating the parameters values that define it. The most important step in the particle swarm algorithm is the method of representing models which should take into account the number, location and variables of parameters to be updated. One example structural system is used to show the applicability of PSO in finding an optimal FEM. An optimal model is defined as the model that has the least number of updated parameters and has the smallest parameter variable variation from the mean material properties. Two different objective functions are used to compare performance of the PSO algorithm.