Discovering stochastic partial differential equations from limited data using variational Bayes inference

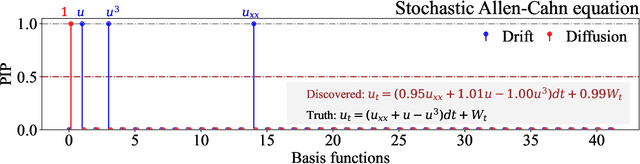
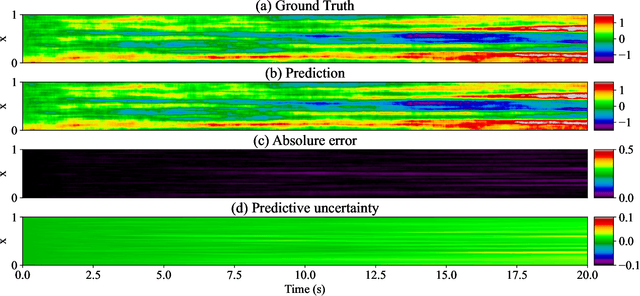
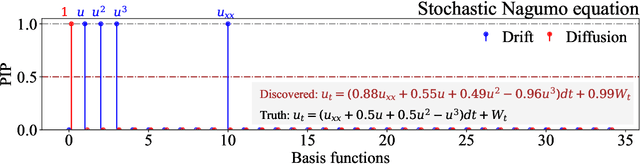
We propose a novel framework for discovering Stochastic Partial Differential Equations (SPDEs) from data. The proposed approach combines the concepts of stochastic calculus, variational Bayes theory, and sparse learning. We propose the extended Kramers-Moyal expansion to express the drift and diffusion terms of an SPDE in terms of state responses and use Spike-and-Slab priors with sparse learning techniques to efficiently and accurately discover the underlying SPDEs. The proposed approach has been applied to three canonical SPDEs, (a) stochastic heat equation, (b) stochastic Allen-Cahn equation, and (c) stochastic Nagumo equation. Our results demonstrate that the proposed approach can accurately identify the underlying SPDEs with limited data. This is the first attempt at discovering SPDEs from data, and it has significant implications for various scientific applications, such as climate modeling, financial forecasting, and chemical kinetics.

MAntRA: A framework for model agnostic reliability analysis

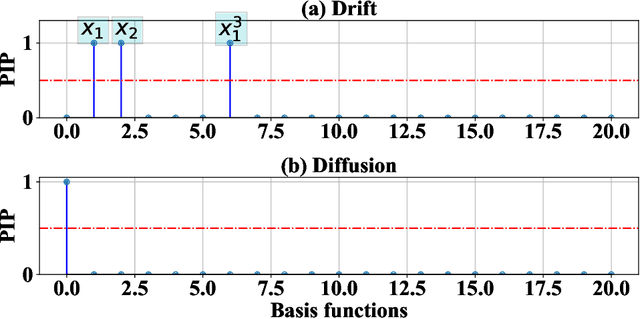
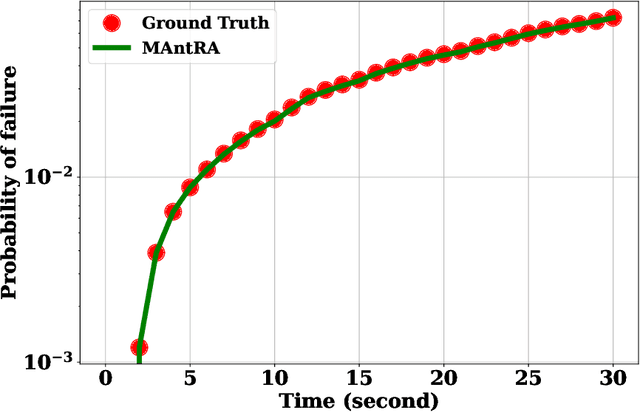
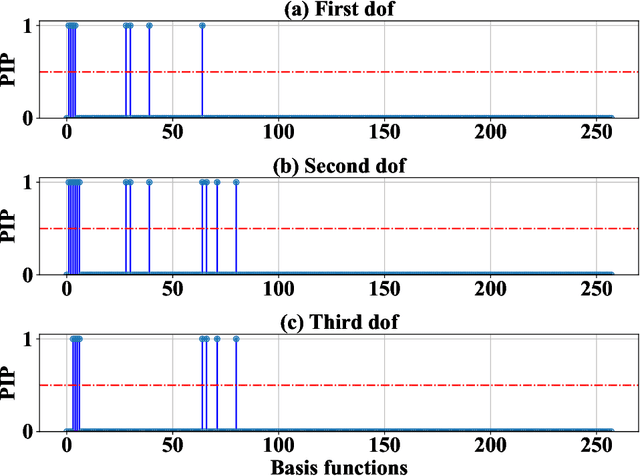
We propose a novel model agnostic data-driven reliability analysis framework for time-dependent reliability analysis. The proposed approach -- referred to as MAntRA -- combines interpretable machine learning, Bayesian statistics, and identifying stochastic dynamic equation to evaluate reliability of stochastically-excited dynamical systems for which the governing physics is \textit{apriori} unknown. A two-stage approach is adopted: in the first stage, an efficient variational Bayesian equation discovery algorithm is developed to determine the governing physics of an underlying stochastic differential equation (SDE) from measured output data. The developed algorithm is efficient and accounts for epistemic uncertainty due to limited and noisy data, and aleatoric uncertainty because of environmental effect and external excitation. In the second stage, the discovered SDE is solved using a stochastic integration scheme and the probability failure is computed. The efficacy of the proposed approach is illustrated on three numerical examples. The results obtained indicate the possible application of the proposed approach for reliability analysis of in-situ and heritage structures from on-site measurements.