Learning Physics for Unveiling Hidden Earthquake Ground Motions via Conditional Generative Modeling

Predicting high-fidelity ground motions for future earthquakes is crucial for seismic hazard assessment and infrastructure resilience. Conventional empirical simulations suffer from sparse sensor distribution and geographically localized earthquake locations, while physics-based methods are computationally intensive and require accurate representations of Earth structures and earthquake sources. We propose a novel artificial intelligence (AI) simulator, Conditional Generative Modeling for Ground Motion (CGM-GM), to synthesize high-frequency and spatially continuous earthquake ground motion waveforms. CGM-GM leverages earthquake magnitudes and geographic coordinates of earthquakes and sensors as inputs, learning complex wave physics and Earth heterogeneities, without explicit physics constraints. This is achieved through a probabilistic autoencoder that captures latent distributions in the time-frequency domain and variational sequential models for prior and posterior distributions. We evaluate the performance of CGM-GM using small-magnitude earthquake records from the San Francisco Bay Area, a region with high seismic risks. CGM-GM demonstrates a strong potential for outperforming a state-of-the-art non-ergodic empirical ground motion model and shows great promise in seismology and beyond.

Bi-fidelity Variational Auto-encoder for Uncertainty Quantification

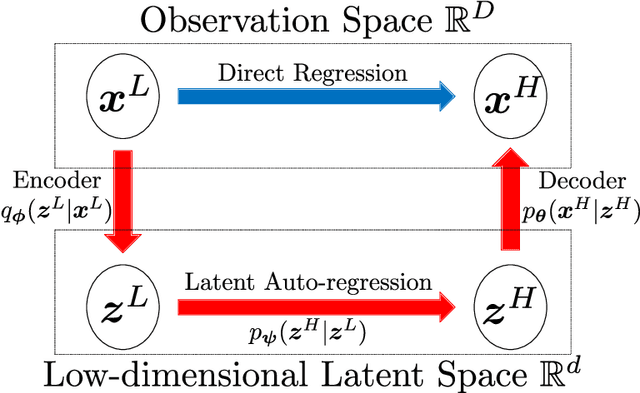
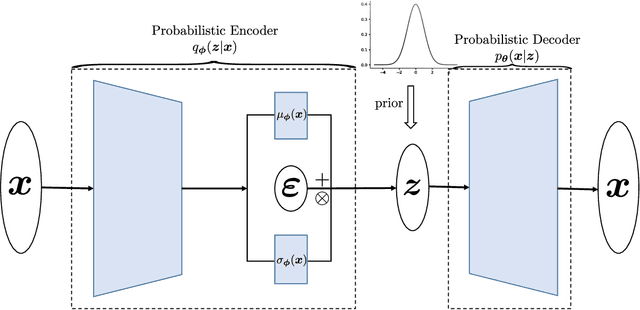
Quantifying the uncertainty of quantities of interest (QoIs) from physical systems is a primary objective in model validation. However, achieving this goal entails balancing the need for computational efficiency with the requirement for numerical accuracy. To address this trade-off, we propose a novel bi-fidelity formulation of variational auto-encoders (BF-VAE) designed to estimate the uncertainty associated with a QoI from low-fidelity (LF) and high-fidelity (HF) samples of the QoI. This model allows for the approximation of the statistics of the HF QoI by leveraging information derived from its LF counterpart. Specifically, we design a bi-fidelity auto-regressive model in the latent space that is integrated within the VAE's probabilistic encoder-decoder structure. An effective algorithm is proposed to maximize the variational lower bound of the HF log-likelihood in the presence of limited HF data, resulting in the synthesis of HF realizations with a reduced computational cost. Additionally, we introduce the concept of the bi-fidelity information bottleneck (BF-IB) to provide an information-theoretic interpretation of the proposed BF-VAE model. Our numerical results demonstrate that BF-VAE leads to considerably improved accuracy, as compared to a VAE trained using only HF data when limited HF data is available.

Sampling-Based Decomposition Algorithms for Arbitrary Tensor Networks

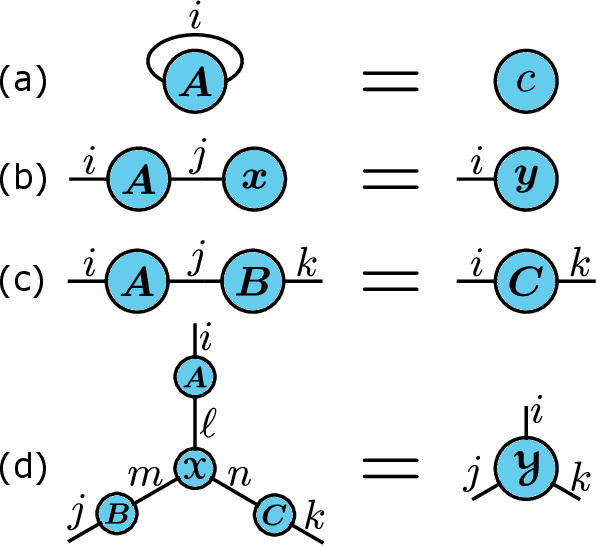
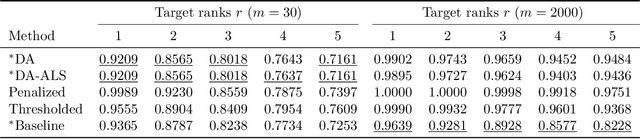
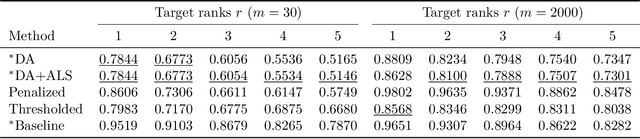
We show how to develop sampling-based alternating least squares (ALS) algorithms for decomposition of tensors into any tensor network (TN) format. Provided the TN format satisfies certain mild assumptions, resulting algorithms will have input sublinear per-iteration cost. Unlike most previous works on sampling-based ALS methods for tensor decomposition, the sampling in our framework is done according to the exact leverage score distribution of the design matrices in the ALS subproblems. We implement and test two tensor decomposition algorithms that use our sampling framework in a feature extraction experiment where we compare them against a number of other decomposition algorithms.

More Efficient Sampling for Tensor Decomposition

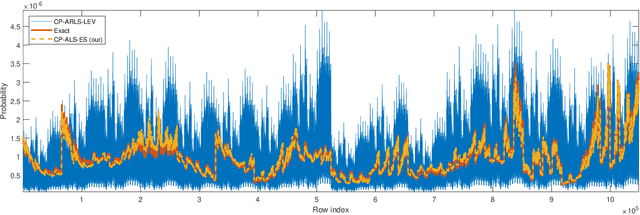
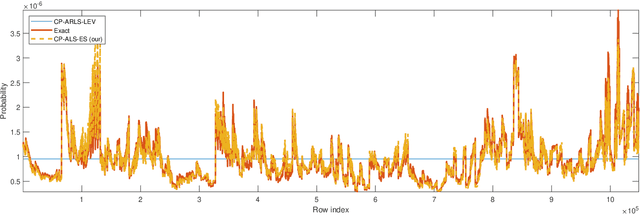
Recent papers have developed alternating least squares (ALS) methods for CP and tensor ring decomposition with a per-iteration cost which is sublinear in the number of input tensor entries for low-rank decomposition. However, the per-iteration cost of these methods still has an exponential dependence on the number of tensor modes. In this paper, we propose sampling-based ALS methods for the CP and tensor ring decompositions whose cost does not have this exponential dependence, thereby significantly improving on the previous state-of-the-art. We provide a detailed theoretical analysis and also apply the methods in a feature extraction experiment.

Superresolution photoacoustic tomography using random speckle illumination and second order moments

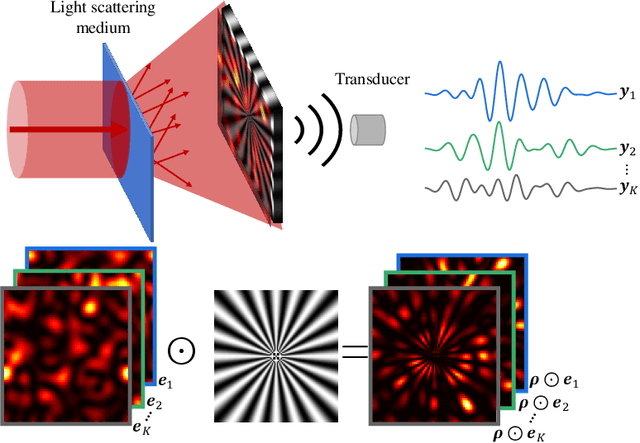
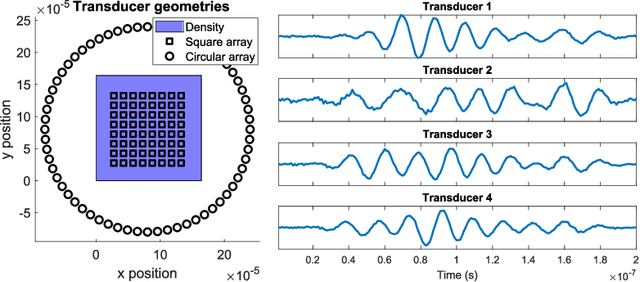
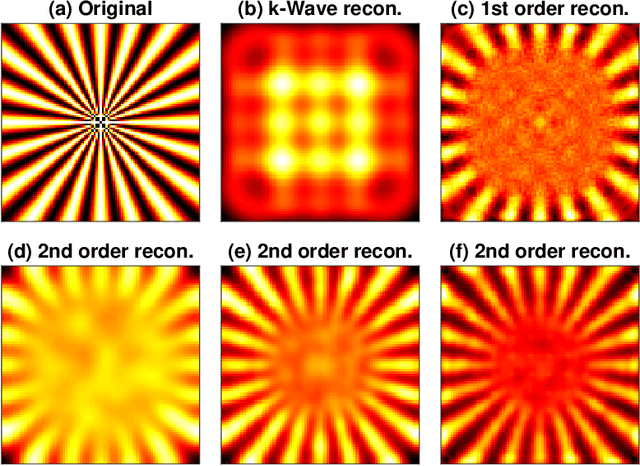
Idier et al. [IEEE Trans. Comput. Imaging 4(1), 2018] propose a method which achieves superresolution in the microscopy setting by leveraging random speckle illumination and knowledge about statistical second order moments for the illumination patterns and model noise. This is achieved without any assumptions on the sparsity of the imaged object. In this paper, we show that their technique can be extended to photoacoustic tomography. We propose a simple algorithm for doing the reconstruction which only requires a small number of linear algebra steps. It is therefore much faster than the iterative method used by Idier et al. We also propose a new representation of the imaged object based on Dirac delta expansion functions.

Binary Matrix Factorization on Special Purpose Hardware

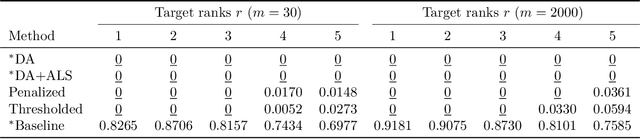
Many fundamental problems in data mining can be reduced to one or more NP-hard combinatorial optimization problems. Recent advances in novel technologies such as quantum and quantum inspired hardware promise a substantial speedup for solving these problems compared to when using general purpose computers but often require the problem to be modeled in a special form, such as an Ising or QUBO model, in order to take advantage of these devices. In this work, we focus on the important binary matrix factorization (BMF) problem which has many applications in data mining. We propose two QUBO formulations for BMF. We show how clustering constraints can easily be incorporated into these formulations. The special purpose hardware we consider is limited in the number of variables it can handle which presents a challenge when factorizing large matrices. We propose a sampling based approach to overcome this challenge, allowing us to factorize large rectangular matrices. We run experiments on the Fujitsu Digital Annealer, a quantum inspired CMOS annealer, on both synthetic and real data, including gene expression data. These experiments show that our approach is able to produce more accurate BMFs than competing methods.

Tensor Graph Convolutional Networks for Prediction on Dynamic Graphs

Many irregular domains such as social networks, financial transactions, neuron connections, and natural language structures are represented as graphs. In recent years, a variety of graph neural networks (GNNs) have been successfully applied for representation learning and prediction on such graphs. However, in many of the applications, the underlying graph changes over time and existing GNNs are inadequate for handling such dynamic graphs. In this paper we propose a novel technique for learning embeddings of dynamic graphs based on a tensor algebra framework. Our method extends the popular graph convolutional network (GCN) for learning representations of dynamic graphs using the recently proposed tensor M-product technique. Theoretical results that establish the connection between the proposed tensor approach and spectral convolution of tensors are developed. Numerical experiments on real datasets demonstrate the usefulness of the proposed method for an edge classification task on dynamic graphs.