Towards Practical Explainability with Cluster Descriptors

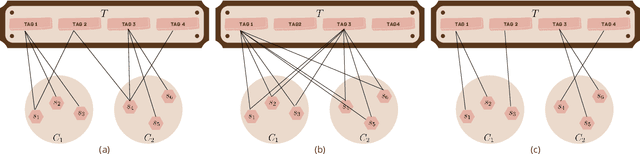
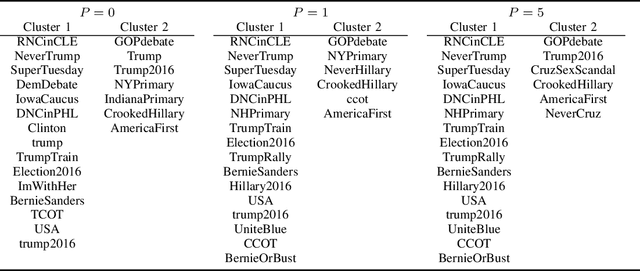
With the rapid development of machine learning, improving its explainability has become a crucial research goal. We study the problem of making the clusters more explainable by investigating the cluster descriptors. Given a set of objects $S$, a clustering of these objects $\pi$, and a set of tags $T$ that have not participated in the clustering algorithm. Each object in $S$ is associated with a subset of $T$. The goal is to find a representative set of tags for each cluster, referred to as the cluster descriptors, with the constraint that these descriptors we find are pairwise disjoint, and the total size of all the descriptors is minimized. In general, this problem is NP-hard. We propose a novel explainability model that reinforces the previous models in such a way that tags that do not contribute to explainability and do not sufficiently distinguish between clusters are not added to the optimal descriptors. The proposed model is formulated as a quadratic unconstrained binary optimization problem which makes it suitable for solving on modern optimization hardware accelerators. We experimentally demonstrate how a proposed explainability model can be solved on specialized hardware for accelerating combinatorial optimization, the Fujitsu Digital Annealer, and use real-life Twitter and PubMed datasets for use cases.

Ising-Based Louvain Method: Clustering Large Graphs with Specialized Hardware

Recent advances in specialized hardware for solving optimization problems such quantum computers, quantum annealers, and CMOS annealers give rise to new ways for solving real-word complex problems. However, given current and near-term hardware limitations, the number of variables required to express a large real-world problem easily exceeds the hardware capabilities, thus hybrid methods are usually developed in order to utilize the hardware. In this work, we advocate for the development of hybrid methods that are built on top of the frameworks of existing state-of-art heuristics, thereby improving these methods. We demonstrate this by building on the so called Louvain method, which is one of the most popular algorithms for the Community detection problem and develop and Ising-based Louvain method. The proposed method outperforms two state-of-the-art community detection algorithms in clustering several small to large-scale graphs. The results show promise in adapting the same optimization approach to other unsupervised learning heuristics to improve their performance.

Binary Matrix Factorization on Special Purpose Hardware

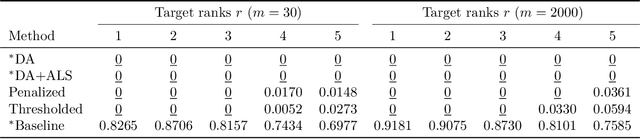
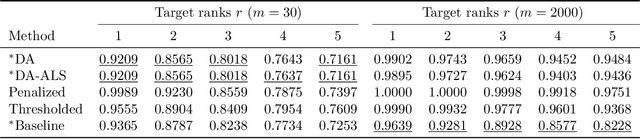
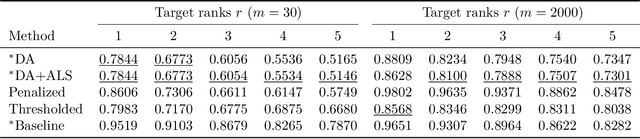
Many fundamental problems in data mining can be reduced to one or more NP-hard combinatorial optimization problems. Recent advances in novel technologies such as quantum and quantum inspired hardware promise a substantial speedup for solving these problems compared to when using general purpose computers but often require the problem to be modeled in a special form, such as an Ising or QUBO model, in order to take advantage of these devices. In this work, we focus on the important binary matrix factorization (BMF) problem which has many applications in data mining. We propose two QUBO formulations for BMF. We show how clustering constraints can easily be incorporated into these formulations. The special purpose hardware we consider is limited in the number of variables it can handle which presents a challenge when factorizing large matrices. We propose a sampling based approach to overcome this challenge, allowing us to factorize large rectangular matrices. We run experiments on the Fujitsu Digital Annealer, a quantum inspired CMOS annealer, on both synthetic and real data, including gene expression data. These experiments show that our approach is able to produce more accurate BMFs than competing methods.