Beyond Single Frames: Can LMMs Comprehend Temporal and Contextual Narratives in Image Sequences?

Large Multimodal Models (LMMs) have achieved remarkable success across various visual-language tasks. However, existing benchmarks predominantly focus on single-image understanding, leaving the analysis of image sequences largely unexplored. To address this limitation, we introduce StripCipher, a comprehensive benchmark designed to evaluate capabilities of LMMs to comprehend and reason over sequential images. StripCipher comprises a human-annotated dataset and three challenging subtasks: visual narrative comprehension, contextual frame prediction, and temporal narrative reordering. Our evaluation of $16$ state-of-the-art LMMs, including GPT-4o and Qwen2.5VL, reveals a significant performance gap compared to human capabilities, particularly in tasks that require reordering shuffled sequential images. For instance, GPT-4o achieves only 23.93% accuracy in the reordering subtask, which is 56.07% lower than human performance. Further quantitative analysis discuss several factors, such as input format of images, affecting the performance of LLMs in sequential understanding, underscoring the fundamental challenges that remain in the development of LMMs.

PDE-Controller: LLMs for Autoformalization and Reasoning of PDEs

While recent AI-for-math has made strides in pure mathematics, areas of applied mathematics, particularly PDEs, remain underexplored despite their significant real-world applications. We present PDE-Controller, a framework that enables large language models (LLMs) to control systems governed by partial differential equations (PDEs). Our approach enables LLMs to transform informal natural language instructions into formal specifications, and then execute reasoning and planning steps to improve the utility of PDE control. We build a holistic solution comprising datasets (both human-written cases and 2 million synthetic samples), math-reasoning models, and novel evaluation metrics, all of which require significant effort. Our PDE-Controller significantly outperforms prompting the latest open-source and GPT models in reasoning, autoformalization, and program synthesis, achieving up to a 62% improvement in utility gain for PDE control. By bridging the gap between language generation and PDE systems, we demonstrate the potential of LLMs in addressing complex scientific and engineering challenges. We will release all data, model checkpoints, and code at https://pde-controller.github.io/.

Effective Large Language Model Debugging with Best-first Tree Search

Large Language Models (LLMs) show promise in code generation tasks. However, their code-writing abilities are often limited in scope: while they can successfully implement simple functions, they struggle with more complex tasks. A fundamental difference with how an LLM writes code, compared to a human programmer, is that it cannot consistently spot and fix bugs. Debugging is a crucial skill for programmers and it enables iterative code refinement towards a correct implementation. In this work, we propose a novel algorithm to enable LLMs to debug their code via self-reflection and search where a model attempts to identify its previous mistakes. Our key contributions are 1) a best-first tree search algorithm with self-reflections (BESTER) that achieves state-of-the-art Pass@1 in three code generation benchmarks. BESTER maintains its superiority when we measure pass rates taking into account additional inference costs incurred by tree search. 2) A novel interpretability study on what self-reflections attend to in buggy programs and how they impact bug fixes, which provides a deeper understanding of the debugging process. 3) An extensive study on when self-reflections are effective in finding bugs.

Learning Physics for Unveiling Hidden Earthquake Ground Motions via Conditional Generative Modeling

Predicting high-fidelity ground motions for future earthquakes is crucial for seismic hazard assessment and infrastructure resilience. Conventional empirical simulations suffer from sparse sensor distribution and geographically localized earthquake locations, while physics-based methods are computationally intensive and require accurate representations of Earth structures and earthquake sources. We propose a novel artificial intelligence (AI) simulator, Conditional Generative Modeling for Ground Motion (CGM-GM), to synthesize high-frequency and spatially continuous earthquake ground motion waveforms. CGM-GM leverages earthquake magnitudes and geographic coordinates of earthquakes and sensors as inputs, learning complex wave physics and Earth heterogeneities, without explicit physics constraints. This is achieved through a probabilistic autoencoder that captures latent distributions in the time-frequency domain and variational sequential models for prior and posterior distributions. We evaluate the performance of CGM-GM using small-magnitude earthquake records from the San Francisco Bay Area, a region with high seismic risks. CGM-GM demonstrates a strong potential for outperforming a state-of-the-art non-ergodic empirical ground motion model and shows great promise in seismology and beyond.

CircuitVAE: Efficient and Scalable Latent Circuit Optimization

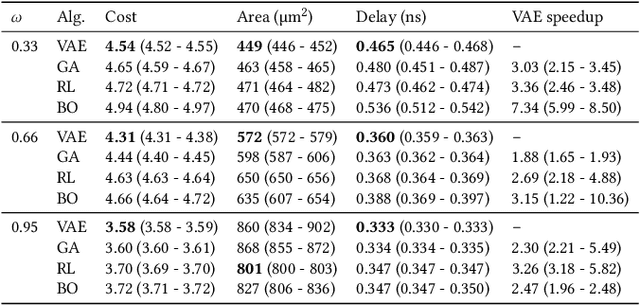
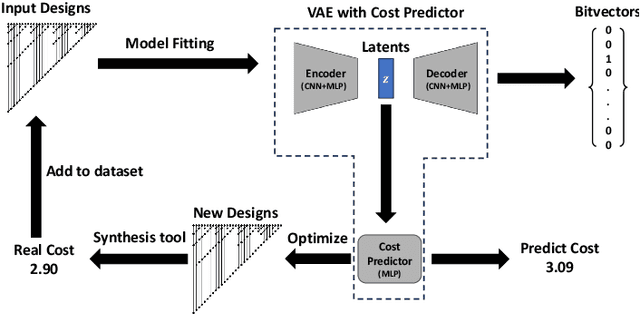
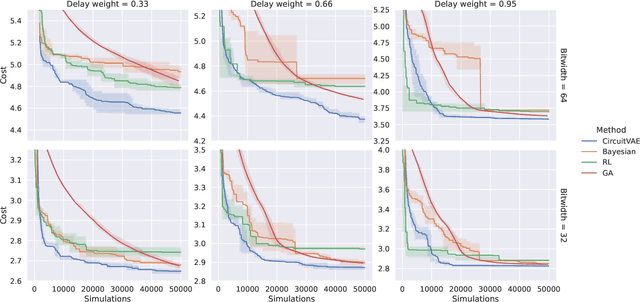
Automatically designing fast and space-efficient digital circuits is challenging because circuits are discrete, must exactly implement the desired logic, and are costly to simulate. We address these challenges with CircuitVAE, a search algorithm that embeds computation graphs in a continuous space and optimizes a learned surrogate of physical simulation by gradient descent. By carefully controlling overfitting of the simulation surrogate and ensuring diverse exploration, our algorithm is highly sample-efficient, yet gracefully scales to large problem instances and high sample budgets. We test CircuitVAE by designing binary adders across a large range of sizes, IO timing constraints, and sample budgets. Our method excels at designing large circuits, where other algorithms struggle: compared to reinforcement learning and genetic algorithms, CircuitVAE typically finds 64-bit adders which are smaller and faster using less than half the sample budget. We also find CircuitVAE can design state-of-the-art adders in a real-world chip, demonstrating that our method can outperform commercial tools in a realistic setting.

Data-Efficient Operator Learning via Unsupervised Pretraining and In-Context Learning

Recent years have witnessed the promise of coupling machine learning methods and physical domain-specific insight for solving scientific problems based on partial differential equations (PDEs). However, being data-intensive, these methods still require a large amount of PDE data. This reintroduces the need for expensive numerical PDE solutions, partially undermining the original goal of avoiding these expensive simulations. In this work, seeking data efficiency, we design unsupervised pretraining and in-context learning methods for PDE operator learning. To reduce the need for training data with simulated solutions, we pretrain neural operators on unlabeled PDE data using reconstruction-based proxy tasks. To improve out-of-distribution performance, we further assist neural operators in flexibly leveraging in-context learning methods, without incurring extra training costs or designs. Extensive empirical evaluations on a diverse set of PDEs demonstrate that our method is highly data-efficient, more generalizable, and even outperforms conventional vision-pretrained models.

Joint-Space Multi-Robot Motion Planning with Learned Decentralized Heuristics

In this paper, we present a method of multi-robot motion planning by biasing centralized, sampling-based tree search with decentralized, data-driven steer and distance heuristics. Over a range of robot and obstacle densities, we evaluate the plain Rapidly-expanding Random Trees (RRT), and variants of our method for double integrator dynamics. We show that whereas plain RRT fails in every instance to plan for $4$ robots, our method can plan for up to 16 robots, corresponding to searching through a very large 65-dimensional space, which validates the effectiveness of data-driven heuristics at combating exponential search space growth. We also find that the heuristic information is complementary; using both heuristics produces search trees with lower failure rates, nodes, and path costs when compared to using each in isolation. These results illustrate the effective decomposition of high-dimensional joint-space motion planning problems into local problems.

Learning Regions of Interest for Bayesian Optimization with Adaptive Level-Set Estimation

We study Bayesian optimization (BO) in high-dimensional and non-stationary scenarios. Existing algorithms for such scenarios typically require extensive hyperparameter tuning, which limits their practical effectiveness. We propose a framework, called BALLET, which adaptively filters for a high-confidence region of interest (ROI) as a superlevel-set of a nonparametric probabilistic model such as a Gaussian process (GP). Our approach is easy to tune, and is able to focus on local region of the optimization space that can be tackled by existing BO methods. The key idea is to use two probabilistic models: a coarse GP to identify the ROI, and a localized GP for optimization within the ROI. We show theoretically that BALLET can efficiently shrink the search space, and can exhibit a tighter regret bound than standard BO without ROI filtering. We demonstrate empirically the effectiveness of BALLET on both synthetic and real-world optimization tasks.

MLNav: Learning to Safely Navigate on Martian Terrains

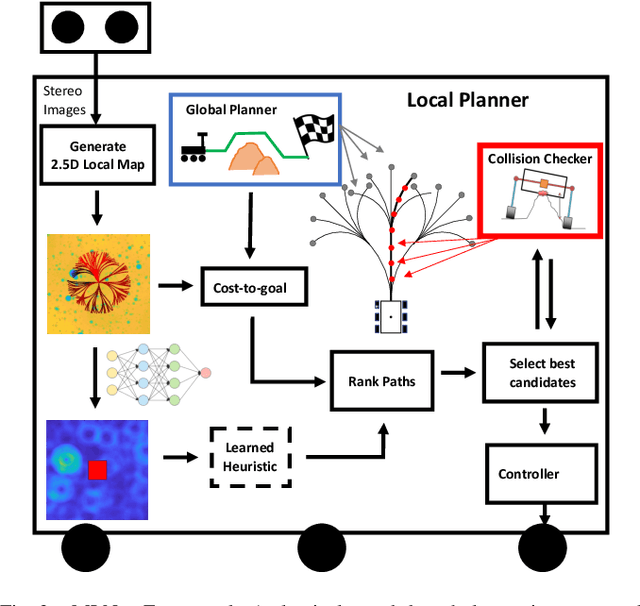
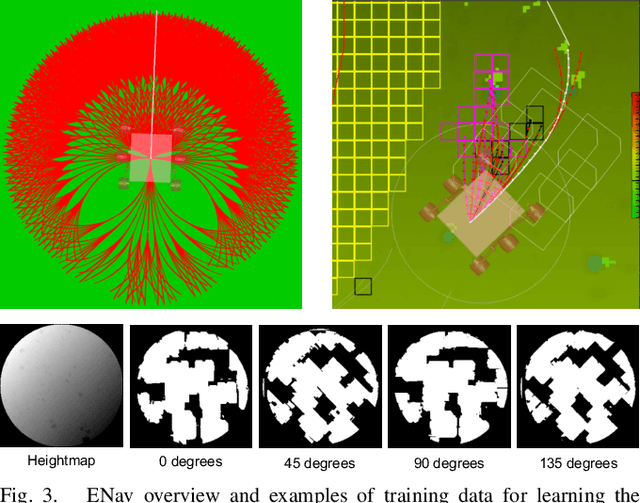
We present MLNav, a learning-enhanced path planning framework for safety-critical and resource-limited systems operating in complex environments, such as rovers navigating on Mars. MLNav makes judicious use of machine learning to enhance the efficiency of path planning while fully respecting safety constraints. In particular, the dominant computational cost in such safety-critical settings is running a model-based safety checker on the proposed paths. Our learned search heuristic can simultaneously predict the feasibility for all path options in a single run, and the model-based safety checker is only invoked on the top-scoring paths. We validate in high-fidelity simulations using both real Martian terrain data collected by the Perseverance rover, as well as a suite of challenging synthetic terrains. Our experiments show that: (i) compared to the baseline ENav path planner on board the Perserverance rover, MLNav can provide a significant improvement in multiple key metrics, such as a 10x reduction in collision checks when navigating real Martian terrains, despite being trained with synthetic terrains; and (ii) MLNav can successfully navigate highly challenging terrains where the baseline ENav fails to find a feasible path before timing out.

Learning Pseudo-Backdoors for Mixed Integer Programs

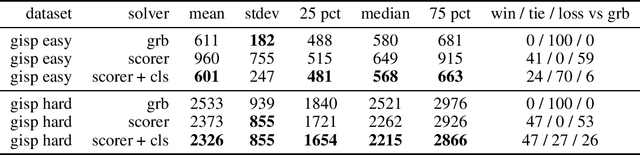
We propose a machine learning approach for quickly solving Mixed Integer Programs (MIP) by learning to prioritize a set of decision variables, which we call pseudo-backdoors, for branching that results in faster solution times. Learning-based approaches have seen success in the area of solving combinatorial optimization problems by being able to flexibly leverage common structures in a given distribution of problems. Our approach takes inspiration from the concept of strong backdoors, which corresponds to a small set of variables such that only branching on these variables yields an optimal integral solution and a proof of optimality. Our notion of pseudo-backdoors corresponds to a small set of variables such that only branching on them leads to faster solve time (which can be solver dependent). A key advantage of pseudo-backdoors over strong backdoors is that they are much amenable to data-driven identification or prediction. Our proposed method learns to estimate the solver performance of a proposed pseudo-backdoor, using a labeled dataset collected on a set of training MIP instances. This model can then be used to identify high-quality pseudo-backdoors on new MIP instances from the same distribution. We evaluate our method on the generalized independent set problems and find that our approach can efficiently identify high-quality pseudo-backdoors. In addition, we compare our learned approach against Gurobi, a state-of-the-art MIP solver, demonstrating that our method can be used to improve solver performance.