P$^2$C$^2$Net: PDE-Preserved Coarse Correction Network for efficient prediction of spatiotemporal dynamics

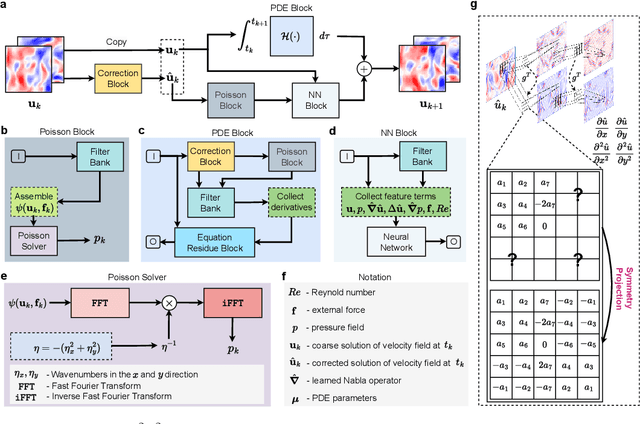
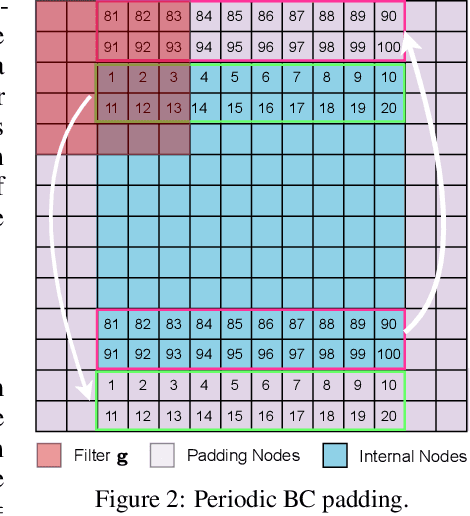
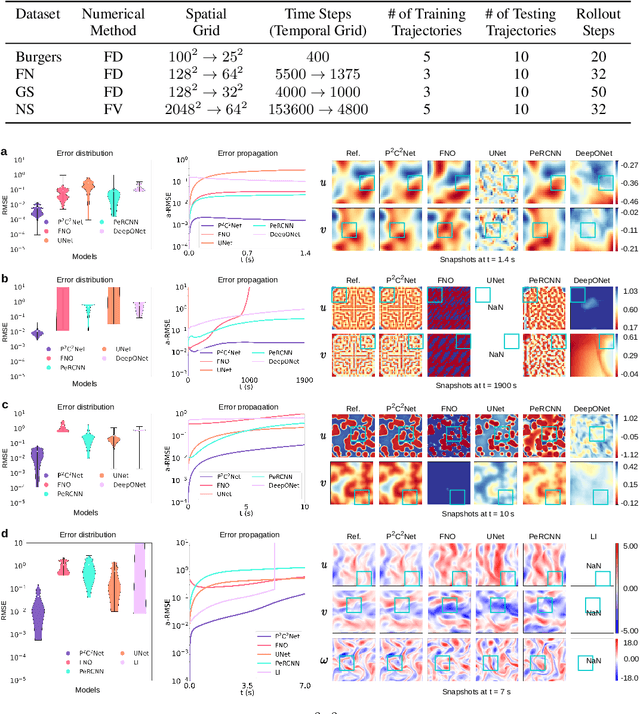
When solving partial differential equations (PDEs), classical numerical methods often require fine mesh grids and small time stepping to meet stability, consistency, and convergence conditions, leading to high computational cost. Recently, machine learning has been increasingly utilized to solve PDE problems, but they often encounter challenges related to interpretability, generalizability, and strong dependency on rich labeled data. Hence, we introduce a new PDE-Preserved Coarse Correction Network (P$^2$C$^2$Net) to efficiently solve spatiotemporal PDE problems on coarse mesh grids in small data regimes. The model consists of two synergistic modules: (1) a trainable PDE block that learns to update the coarse solution (i.e., the system state), based on a high-order numerical scheme with boundary condition encoding, and (2) a neural network block that consistently corrects the solution on the fly. In particular, we propose a learnable symmetric Conv filter, with weights shared over the entire model, to accurately estimate the spatial derivatives of PDE based on the neural-corrected system state. The resulting physics-encoded model is capable of handling limited training data (e.g., 3--5 trajectories) and accelerates the prediction of PDE solutions on coarse spatiotemporal grids while maintaining a high accuracy. P$^2$C$^2$Net achieves consistent state-of-the-art performance with over 50\% gain (e.g., in terms of relative prediction error) across four datasets covering complex reaction-diffusion processes and turbulent flows.

Model Balancing Helps Low-data Training and Fine-tuning

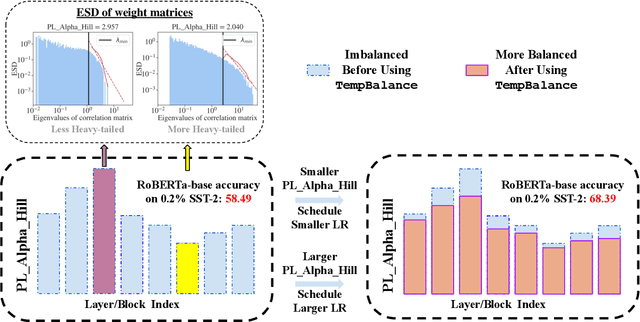
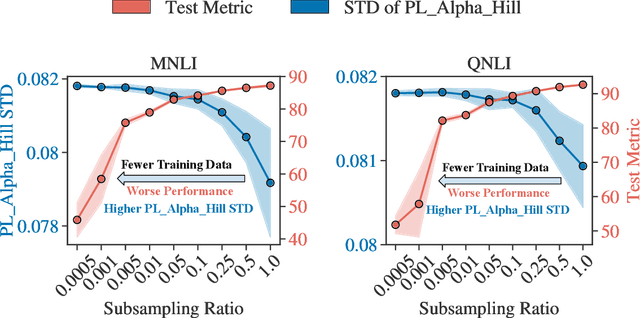
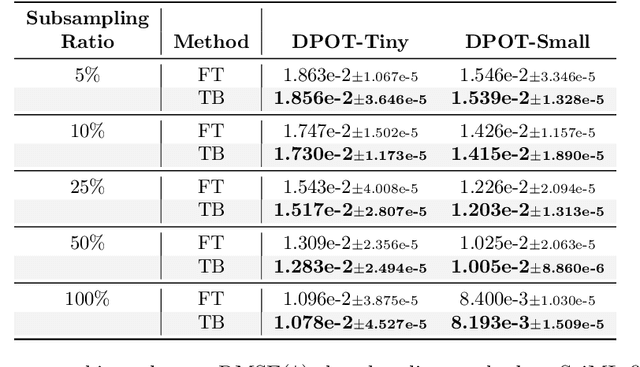
Recent advances in foundation models have emphasized the need to align pre-trained models with specialized domains using small, curated datasets. Studies on these foundation models underscore the importance of low-data training and fine-tuning. This topic, well-known in natural language processing (NLP), has also gained increasing attention in the emerging field of scientific machine learning (SciML). To address the limitations of low-data training and fine-tuning, we draw inspiration from Heavy-Tailed Self-Regularization (HT-SR) theory, analyzing the shape of empirical spectral densities (ESDs) and revealing an imbalance in training quality across different model layers. To mitigate this issue, we adapt a recently proposed layer-wise learning rate scheduler, TempBalance, which effectively balances training quality across layers and enhances low-data training and fine-tuning for both NLP and SciML tasks. Notably, TempBalance demonstrates increasing performance gains as the amount of available tuning data decreases. Comparative analyses further highlight the effectiveness of TempBalance and its adaptability as an "add-on" method for improving model performance.

Learning Physics for Unveiling Hidden Earthquake Ground Motions via Conditional Generative Modeling

Predicting high-fidelity ground motions for future earthquakes is crucial for seismic hazard assessment and infrastructure resilience. Conventional empirical simulations suffer from sparse sensor distribution and geographically localized earthquake locations, while physics-based methods are computationally intensive and require accurate representations of Earth structures and earthquake sources. We propose a novel artificial intelligence (AI) simulator, Conditional Generative Modeling for Ground Motion (CGM-GM), to synthesize high-frequency and spatially continuous earthquake ground motion waveforms. CGM-GM leverages earthquake magnitudes and geographic coordinates of earthquakes and sensors as inputs, learning complex wave physics and Earth heterogeneities, without explicit physics constraints. This is achieved through a probabilistic autoencoder that captures latent distributions in the time-frequency domain and variational sequential models for prior and posterior distributions. We evaluate the performance of CGM-GM using small-magnitude earthquake records from the San Francisco Bay Area, a region with high seismic risks. CGM-GM demonstrates a strong potential for outperforming a state-of-the-art non-ergodic empirical ground motion model and shows great promise in seismology and beyond.

WaveCastNet: An AI-enabled Wavefield Forecasting Framework for Earthquake Early Warning

Large earthquakes can be destructive and quickly wreak havoc on a landscape. To mitigate immediate threats, early warning systems have been developed to alert residents, emergency responders, and critical infrastructure operators seconds to a minute before seismic waves arrive. These warnings provide time to take precautions and prevent damage. The success of these systems relies on fast, accurate predictions of ground motion intensities, which is challenging due to the complex physics of earthquakes, wave propagation, and their intricate spatial and temporal interactions. To improve early warning, we propose a novel AI-enabled framework, WaveCastNet, for forecasting ground motions from large earthquakes. WaveCastNet integrates a novel convolutional Long Expressive Memory (ConvLEM) model into a sequence to sequence (seq2seq) forecasting framework to model long-term dependencies and multi-scale patterns in both space and time. WaveCastNet, which shares weights across spatial and temporal dimensions, requires fewer parameters compared to more resource-intensive models like transformers and thus, in turn, reduces inference times. Importantly, WaveCastNet also generalizes better than transformer-based models to different seismic scenarios, including to more rare and critical situations with higher magnitude earthquakes. Our results using simulated data from the San Francisco Bay Area demonstrate the capability to rapidly predict the intensity and timing of destructive ground motions. Importantly, our proposed approach does not require estimating earthquake magnitudes and epicenters, which are prone to errors using conventional approaches; nor does it require empirical ground motion models, which fail to capture strongly heterogeneous wave propagation effects.

Reasoning-Enhanced Object-Centric Learning for Videos

Object-centric learning aims to break down complex visual scenes into more manageable object representations, enhancing the understanding and reasoning abilities of machine learning systems toward the physical world. Recently, slot-based video models have demonstrated remarkable proficiency in segmenting and tracking objects, but they overlook the importance of the effective reasoning module. In the real world, reasoning and predictive abilities play a crucial role in human perception and object tracking; in particular, these abilities are closely related to human intuitive physics. Inspired by this, we designed a novel reasoning module called the Slot-based Time-Space Transformer with Memory buffer (STATM) to enhance the model's perception ability in complex scenes. The memory buffer primarily serves as storage for slot information from upstream modules, the Slot-based Time-Space Transformer makes predictions through slot-based spatiotemporal attention computations and fusion. Our experiment results on various datasets show that STATM can significantly enhance object-centric learning capabilities of slot-based video models.

Physics-Informed Machine Learning for Seismic Response Prediction OF Nonlinear Steel Moment Resisting Frame Structures

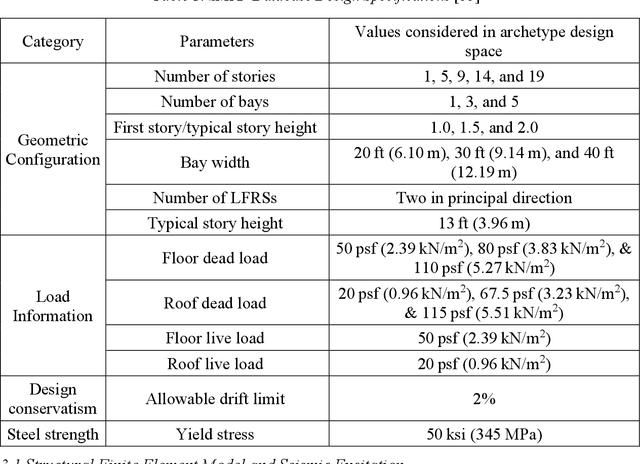
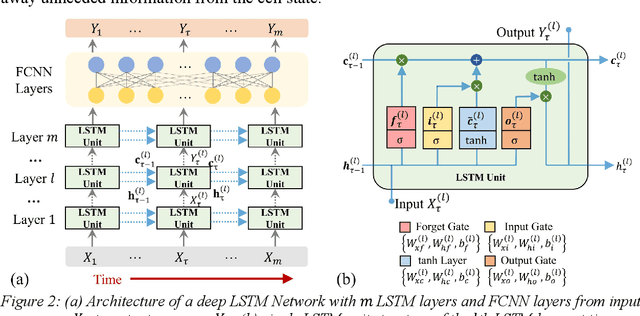
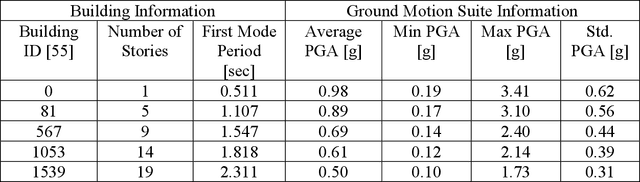
There is a growing interest in utilizing machine learning (ML) methods for structural metamodeling due to the substantial computational cost of traditional numerical simulations. The existing data-driven strategies show potential limitations to the model robustness and interpretability as well as the dependency of rich data. To address these challenges, this paper presents a novel physics-informed machine learning (PiML) method, which incorporates scientific principles and physical laws into deep neural networks for modeling seismic responses of nonlinear structures. The basic concept is to constrain the solution space of the ML model within known physical bounds. This is made possible with three main features, namely, model order reduction, a long short-term memory (LSTM) networks, and Newton's second law (e.g., the equation of motion). Model order reduction is essential for handling structural systems with inherent redundancy and enhancing model efficiency. The LSTM network captures temporal dependencies, enabling accurate prediction of time series responses. The equation of motion is manipulated to learn system nonlinearities and confines the solution space within physically interpretable results. These features enable model training with relatively sparse data and offer benefits in terms of accuracy, interpretability, and robustness. Furthermore, a dataset of seismically designed archetype ductile planar steel moment resistant frames under horizontal seismic loading, available in the DesignSafe-CI Database, is considered for evaluation of the proposed method. The resulting metamodel is capable of handling more complex data compared to existing physics-guided LSTM models and outperforms other non-physics data-driven neural networks.

Data-Efficient Operator Learning via Unsupervised Pretraining and In-Context Learning

Recent years have witnessed the promise of coupling machine learning methods and physical domain-specific insight for solving scientific problems based on partial differential equations (PDEs). However, being data-intensive, these methods still require a large amount of PDE data. This reintroduces the need for expensive numerical PDE solutions, partially undermining the original goal of avoiding these expensive simulations. In this work, seeking data efficiency, we design unsupervised pretraining and in-context learning methods for PDE operator learning. To reduce the need for training data with simulated solutions, we pretrain neural operators on unlabeled PDE data using reconstruction-based proxy tasks. To improve out-of-distribution performance, we further assist neural operators in flexibly leveraging in-context learning methods, without incurring extra training costs or designs. Extensive empirical evaluations on a diverse set of PDEs demonstrate that our method is highly data-efficient, more generalizable, and even outperforms conventional vision-pretrained models.

Generative Modeling of Regular and Irregular Time Series Data via Koopman VAEs

Generating realistic time series data is important for many engineering and scientific applications. Existing work tackles this problem using generative adversarial networks (GANs). However, GANs are often unstable during training, and they can suffer from mode collapse. While variational autoencoders (VAEs) are known to be more robust to these issues, they are (surprisingly) less often considered for time series generation. In this work, we introduce Koopman VAE (KVAE), a new generative framework that is based on a novel design for the model prior, and that can be optimized for either regular and irregular training data. Inspired by Koopman theory, we represent the latent conditional prior dynamics using a linear map. Our approach enhances generative modeling with two desired features: (i) incorporating domain knowledge can be achieved by leverageing spectral tools that prescribe constraints on the eigenvalues of the linear map; and (ii) studying the qualitative behavior and stablity of the system can be performed using tools from dynamical systems theory. Our results show that KVAE outperforms state-of-the-art GAN and VAE methods across several challenging synthetic and real-world time series generation benchmarks. Whether trained on regular or irregular data, KVAE generates time series that improve both discriminative and predictive metrics. We also present visual evidence suggesting that KVAE learns probability density functions that better approximate empirical ground truth distributions.

SuperBench: A Super-Resolution Benchmark Dataset for Scientific Machine Learning

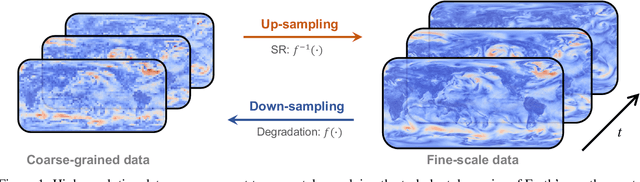
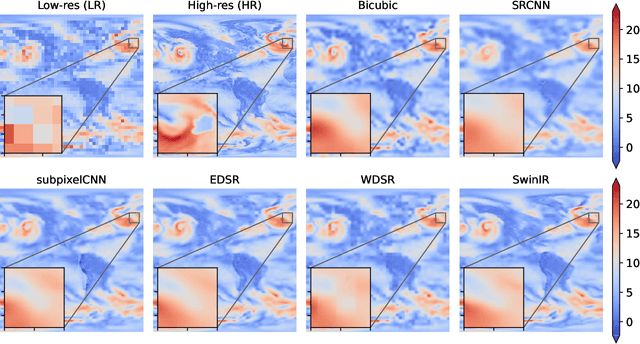
Super-Resolution (SR) techniques aim to enhance data resolution, enabling the retrieval of finer details, and improving the overall quality and fidelity of the data representation. There is growing interest in applying SR methods to complex spatiotemporal systems within the Scientific Machine Learning (SciML) community, with the hope of accelerating numerical simulations and/or improving forecasts in weather, climate, and related areas. However, the lack of standardized benchmark datasets for comparing and validating SR methods hinders progress and adoption in SciML. To address this, we introduce SuperBench, the first benchmark dataset featuring high-resolution datasets (up to $2048\times2048$ dimensions), including data from fluid flows, cosmology, and weather. Here, we focus on validating spatial SR performance from data-centric and physics-preserved perspectives, as well as assessing robustness to data degradation tasks. While deep learning-based SR methods (developed in the computer vision community) excel on certain tasks, despite relatively limited prior physics information, we identify limitations of these methods in accurately capturing intricate fine-scale features and preserving fundamental physical properties and constraints in scientific data. These shortcomings highlight the importance and subtlety of incorporating domain knowledge into ML models. We anticipate that SuperBench will significantly advance SR methods for scientific tasks.

Physics-informed neural network for seismic wave inversion in layered semi-infinite domain

Estimating the material distribution of Earth's subsurface is a challenging task in seismology and earthquake engineering. The recent development of physics-informed neural network (PINN) has shed new light on seismic inversion. In this paper, we present a PINN framework for seismic wave inversion in layered (1D) semi-infinite domain. The absorbing boundary condition is incorporated into the network as a soft regularizer for avoiding excessive computation. In specific, we design a lightweight network to learn the unknown material distribution and a deep neural network to approximate solution variables. The entire network is end-to-end and constrained by both sparse measurement data and the underlying physical laws (i.e., governing equations and initial/boundary conditions). Various experiments have been conducted to validate the effectiveness of our proposed approach for inverse modeling of seismic wave propagation in 1D semi-infinite domain.