MultiPDENet: PDE-embedded Learning with Multi-time-stepping for Accelerated Flow Simulation

Solving partial differential equations (PDEs) by numerical methods meet computational cost challenge for getting the accurate solution since fine grids and small time steps are required. Machine learning can accelerate this process, but struggle with weak generalizability, interpretability, and data dependency, as well as suffer in long-term prediction. To this end, we propose a PDE-embedded network with multiscale time stepping (MultiPDENet), which fuses the scheme of numerical methods and machine learning, for accelerated simulation of flows. In particular, we design a convolutional filter based on the structure of finite difference stencils with a small number of parameters to optimize, which estimates the equivalent form of spatial derivative on a coarse grid to minimize the equation's residual. A Physics Block with a 4th-order Runge-Kutta integrator at the fine time scale is established that embeds the structure of PDEs to guide the prediction. To alleviate the curse of temporal error accumulation in long-term prediction, we introduce a multiscale time integration approach, where a neural network is used to correct the prediction error at a coarse time scale. Experiments across various PDE systems, including the Navier-Stokes equations, demonstrate that MultiPDENet can accurately predict long-term spatiotemporal dynamics, even given small and incomplete training data, e.g., spatiotemporally down-sampled datasets. MultiPDENet achieves the state-of-the-art performance compared with other neural baseline models, also with clear speedup compared to classical numerical methods.

P$^2$C$^2$Net: PDE-Preserved Coarse Correction Network for efficient prediction of spatiotemporal dynamics

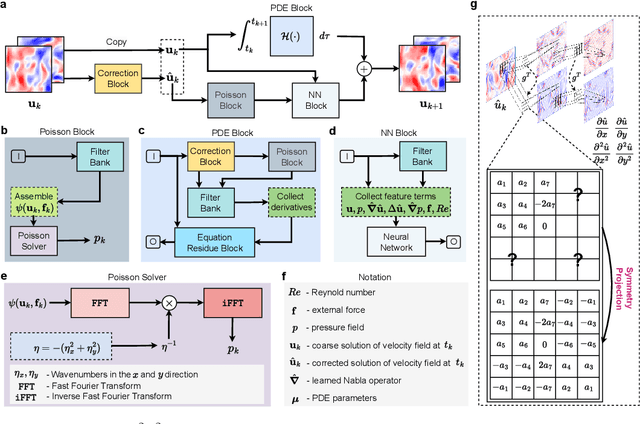
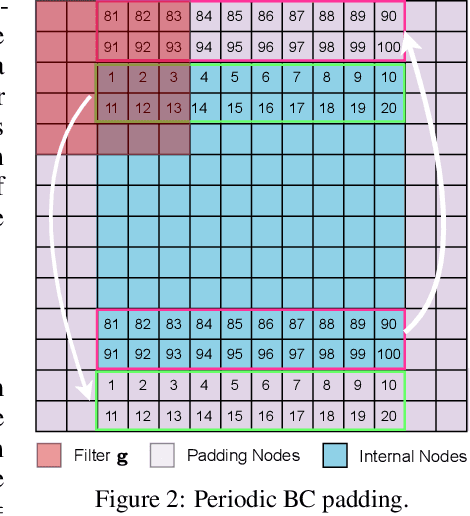
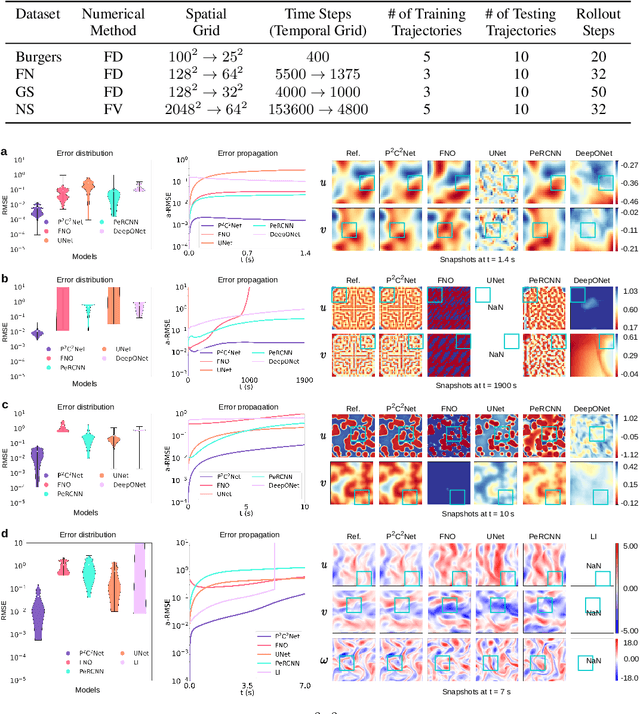
When solving partial differential equations (PDEs), classical numerical methods often require fine mesh grids and small time stepping to meet stability, consistency, and convergence conditions, leading to high computational cost. Recently, machine learning has been increasingly utilized to solve PDE problems, but they often encounter challenges related to interpretability, generalizability, and strong dependency on rich labeled data. Hence, we introduce a new PDE-Preserved Coarse Correction Network (P$^2$C$^2$Net) to efficiently solve spatiotemporal PDE problems on coarse mesh grids in small data regimes. The model consists of two synergistic modules: (1) a trainable PDE block that learns to update the coarse solution (i.e., the system state), based on a high-order numerical scheme with boundary condition encoding, and (2) a neural network block that consistently corrects the solution on the fly. In particular, we propose a learnable symmetric Conv filter, with weights shared over the entire model, to accurately estimate the spatial derivatives of PDE based on the neural-corrected system state. The resulting physics-encoded model is capable of handling limited training data (e.g., 3--5 trajectories) and accelerates the prediction of PDE solutions on coarse spatiotemporal grids while maintaining a high accuracy. P$^2$C$^2$Net achieves consistent state-of-the-art performance with over 50\% gain (e.g., in terms of relative prediction error) across four datasets covering complex reaction-diffusion processes and turbulent flows.

PhyMPGN: Physics-encoded Message Passing Graph Network for spatiotemporal PDE systems

Solving partial differential equations (PDEs) serves as a cornerstone for modeling complex dynamical systems. Recent progresses have demonstrated grand benefits of data-driven neural-based models for predicting spatiotemporal dynamics (e.g., tremendous speedup gain compared with classical numerical methods). However, most existing neural models rely on rich training data, have limited extrapolation and generalization abilities, and suffer to produce precise or reliable physical prediction under intricate conditions (e.g., irregular mesh or geometry, complex boundary conditions, diverse PDE parameters, etc.). To this end, we propose a new graph learning approach, namely, Physics-encoded Message Passing Graph Network (PhyMPGN), to model spatiotemporal PDE systems on irregular meshes given small training datasets. Specifically, we incorporate a GNN into a numerical integrator to approximate the temporal marching of spatiotemporal dynamics for a given PDE system. Considering that many physical phenomena are governed by diffusion processes, we further design a learnable Laplace block, which encodes the discrete Laplace-Beltrami operator, to aid and guide the GNN learning in a physically feasible solution space. A boundary condition padding strategy is also designed to improve the model convergence and accuracy. Extensive experiments demonstrate that PhyMPGN is capable of accurately predicting various types of spatiotemporal dynamics on coarse unstructured meshes, consistently achieves the state-of-the-art results, and outperforms other baselines with considerable gains.