Xin-Yang Liu
Multi-fidelity Reinforcement Learning Control for Complex Dynamical Systems
Apr 08, 2025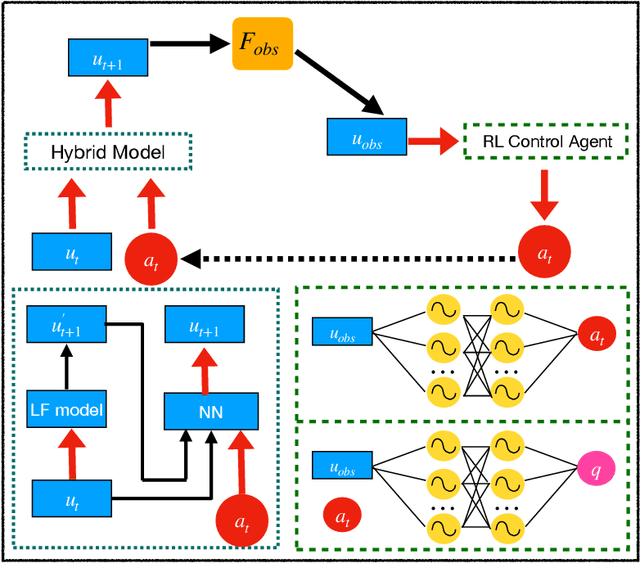
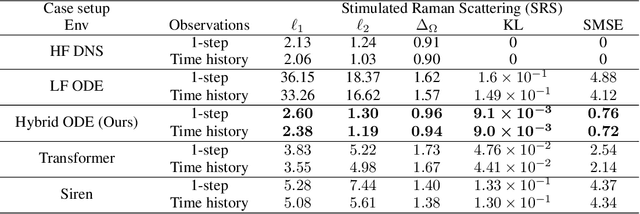
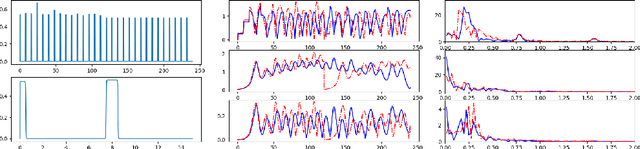
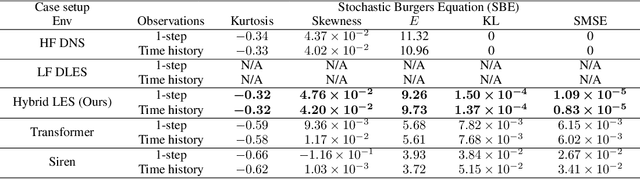
Abstract:Controlling instabilities in complex dynamical systems is challenging in scientific and engineering applications. Deep reinforcement learning (DRL) has seen promising results for applications in different scientific applications. The many-query nature of control tasks requires multiple interactions with real environments of the underlying physics. However, it is usually sparse to collect from the experiments or expensive to simulate for complex dynamics. Alternatively, controlling surrogate modeling could mitigate the computational cost issue. However, a fast and accurate learning-based model by offline training makes it very hard to get accurate pointwise dynamics when the dynamics are chaotic. To bridge this gap, the current work proposes a multi-fidelity reinforcement learning (MFRL) framework that leverages differentiable hybrid models for control tasks, where a physics-based hybrid model is corrected by limited high-fidelity data. We also proposed a spectrum-based reward function for RL learning. The effect of the proposed framework is demonstrated on two complex dynamics in physics. The statistics of the MFRL control result match that computed from many-query evaluations of the high-fidelity environments and outperform other SOTA baselines.
CoNFiLD-inlet: Synthetic Turbulence Inflow Using Generative Latent Diffusion Models with Neural Fields
Nov 21, 2024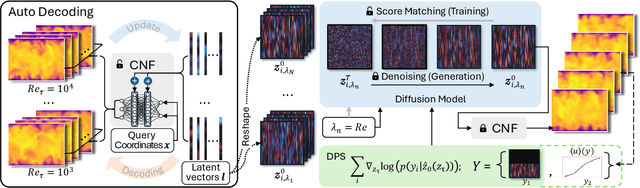
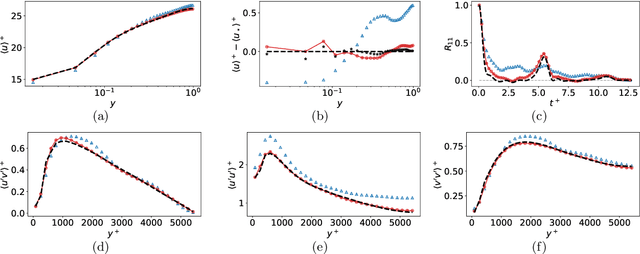
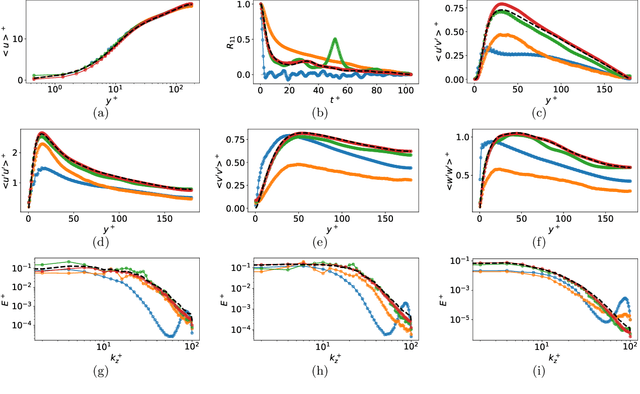
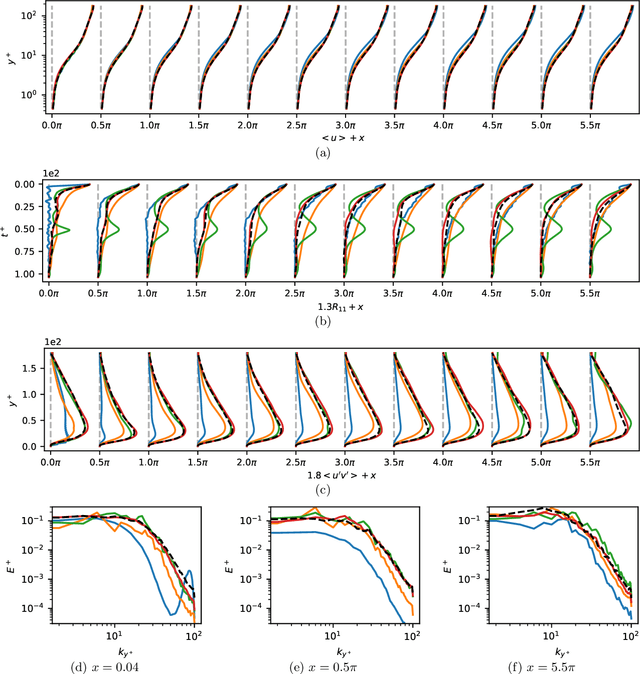
Abstract:Eddy-resolving turbulence simulations require stochastic inflow conditions that accurately replicate the complex, multi-scale structures of turbulence. Traditional recycling-based methods rely on computationally expensive precursor simulations, while existing synthetic inflow generators often fail to reproduce realistic coherent structures of turbulence. Recent advances in deep learning (DL) have opened new possibilities for inflow turbulence generation, yet many DL-based methods rely on deterministic, autoregressive frameworks prone to error accumulation, resulting in poor robustness for long-term predictions. In this work, we present CoNFiLD-inlet, a novel DL-based inflow turbulence generator that integrates diffusion models with a conditional neural field (CNF)-encoded latent space to produce realistic, stochastic inflow turbulence. By parameterizing inflow conditions using Reynolds numbers, CoNFiLD-inlet generalizes effectively across a wide range of Reynolds numbers ($Re_\tau$ between $10^3$ and $10^4$) without requiring retraining or parameter tuning. Comprehensive validation through a priori and a posteriori tests in Direct Numerical Simulation (DNS) and Wall-Modeled Large Eddy Simulation (WMLES) demonstrates its high fidelity, robustness, and scalability, positioning it as an efficient and versatile solution for inflow turbulence synthesis.
P$^2$C$^2$Net: PDE-Preserved Coarse Correction Network for efficient prediction of spatiotemporal dynamics
Oct 29, 2024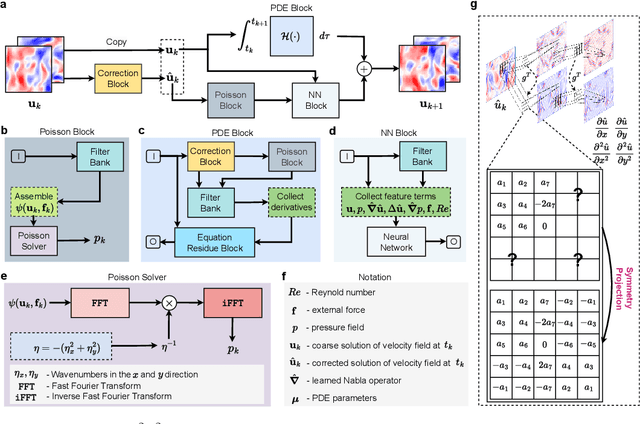
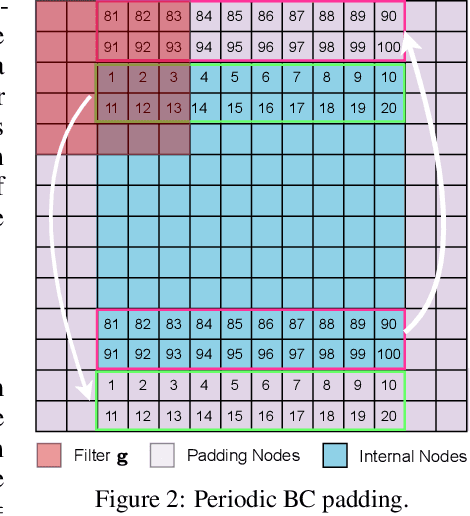

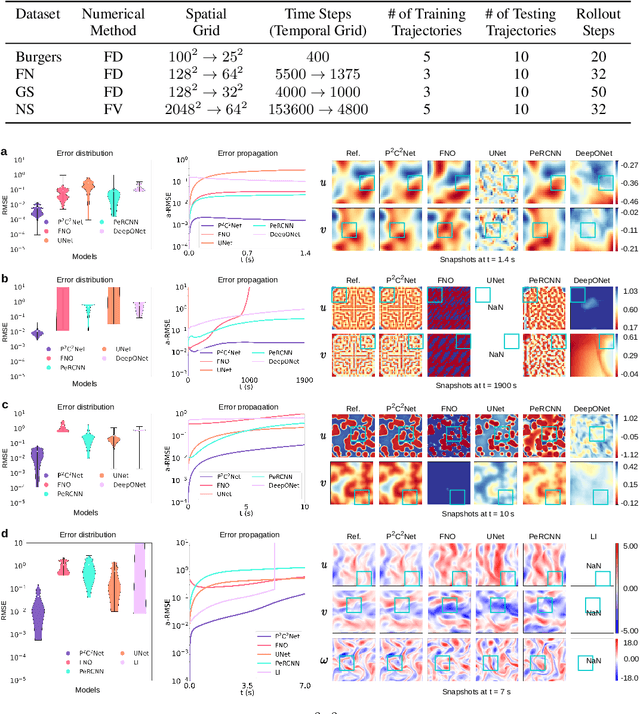
Abstract:When solving partial differential equations (PDEs), classical numerical methods often require fine mesh grids and small time stepping to meet stability, consistency, and convergence conditions, leading to high computational cost. Recently, machine learning has been increasingly utilized to solve PDE problems, but they often encounter challenges related to interpretability, generalizability, and strong dependency on rich labeled data. Hence, we introduce a new PDE-Preserved Coarse Correction Network (P$^2$C$^2$Net) to efficiently solve spatiotemporal PDE problems on coarse mesh grids in small data regimes. The model consists of two synergistic modules: (1) a trainable PDE block that learns to update the coarse solution (i.e., the system state), based on a high-order numerical scheme with boundary condition encoding, and (2) a neural network block that consistently corrects the solution on the fly. In particular, we propose a learnable symmetric Conv filter, with weights shared over the entire model, to accurately estimate the spatial derivatives of PDE based on the neural-corrected system state. The resulting physics-encoded model is capable of handling limited training data (e.g., 3--5 trajectories) and accelerates the prediction of PDE solutions on coarse spatiotemporal grids while maintaining a high accuracy. P$^2$C$^2$Net achieves consistent state-of-the-art performance with over 50\% gain (e.g., in terms of relative prediction error) across four datasets covering complex reaction-diffusion processes and turbulent flows.
Asynchronous Parallel Reinforcement Learning for Optimizing Propulsive Performance in Fin Ray Control
Jan 21, 2024Abstract:Fish fin rays constitute a sophisticated control system for ray-finned fish, facilitating versatile locomotion within complex fluid environments. Despite extensive research on the kinematics and hydrodynamics of fish locomotion, the intricate control strategies in fin-ray actuation remain largely unexplored. While deep reinforcement learning (DRL) has demonstrated potential in managing complex nonlinear dynamics; its trial-and-error nature limits its application to problems involving computationally demanding environmental interactions. This study introduces a cutting-edge off-policy DRL algorithm, interacting with a fluid-structure interaction (FSI) environment to acquire intricate fin-ray control strategies tailored for various propulsive performance objectives. To enhance training efficiency and enable scalable parallelism, an innovative asynchronous parallel training (APT) strategy is proposed, which fully decouples FSI environment interactions and policy/value network optimization. The results demonstrated the success of the proposed method in discovering optimal complex policies for fin-ray actuation control, resulting in a superior propulsive performance compared to the optimal sinusoidal actuation function identified through a parametric grid search. The merit and effectiveness of the APT approach are also showcased through comprehensive comparison with conventional DRL training strategies in numerical experiments of controlling nonlinear dynamics.
Predicting parametric spatiotemporal dynamics by multi-resolution PDE structure-preserved deep learning
May 09, 2022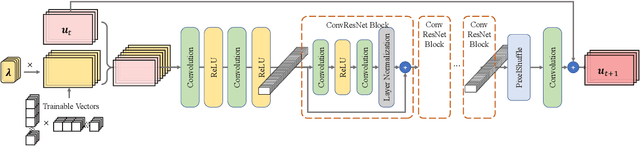
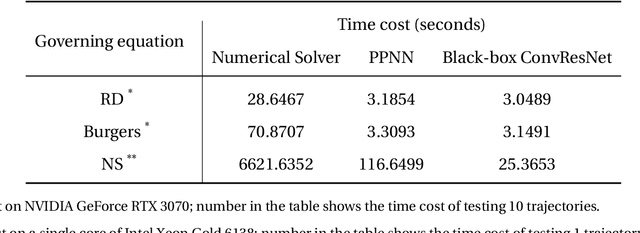
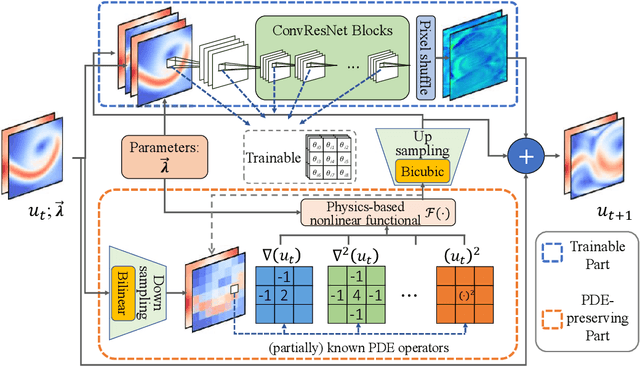
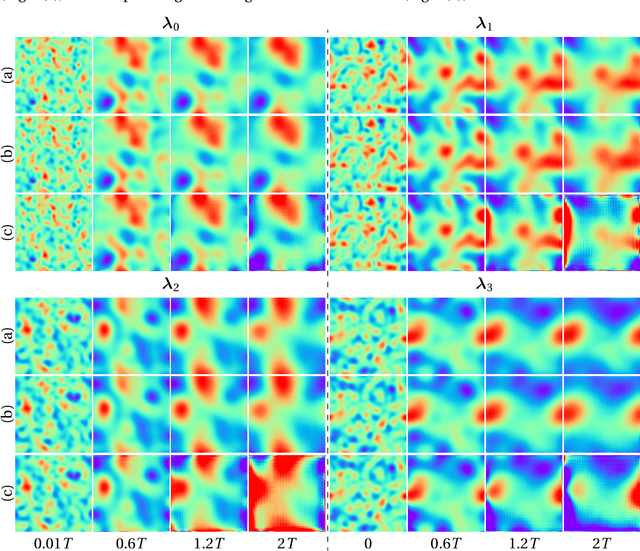
Abstract:Although recent advances in deep learning (DL) have shown a great promise for learning physics exhibiting complex spatiotemporal dynamics, the high training cost, unsatisfying extrapolability for long-term predictions, and poor generalizability in out-of-sample regimes significantly limit their applications in science/engineering problems. A more promising way is to leverage available physical prior and domain knowledge to develop scientific DL models, known as physics-informed deep learning (PiDL). In most existing PiDL frameworks, e.g., physics-informed neural networks, the physics prior is mainly utilized to regularize neural network training by incorporating governing equations into the loss function in a soft manner. In this work, we propose a new direction to leverage physics prior knowledge by baking the mathematical structures of governing equations into the neural network architecture design. In particular, we develop a novel PDE-preserved neural network (PPNN) for rapidly predicting parametric spatiotemporal dynamics, given the governing PDEs are (partially) known. The discretized PDE structures are preserved in PPNN as convolutional residual network (ConvResNet) blocks, which are formulated in a multi-resolution setting. This physics-inspired learning architecture design endows PPNN with excellent generalizability and long-term prediction accuracy compared to the state-of-the-art black-box ConvResNet baseline. The effectiveness and merit of the proposed methods have been demonstrated over a handful of spatiotemporal dynamical systems governed by unsteady PDEs, including reaction-diffusion, Burgers', and Navier-Stokes equations.
Physics-informed Dyna-Style Model-Based Deep Reinforcement Learning for Dynamic Control
Jul 31, 2021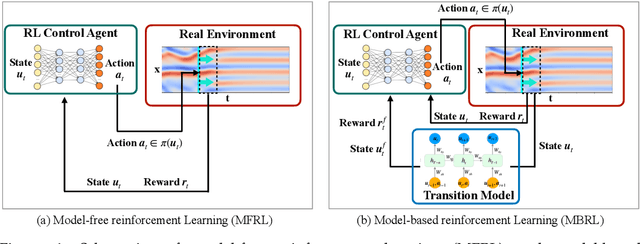

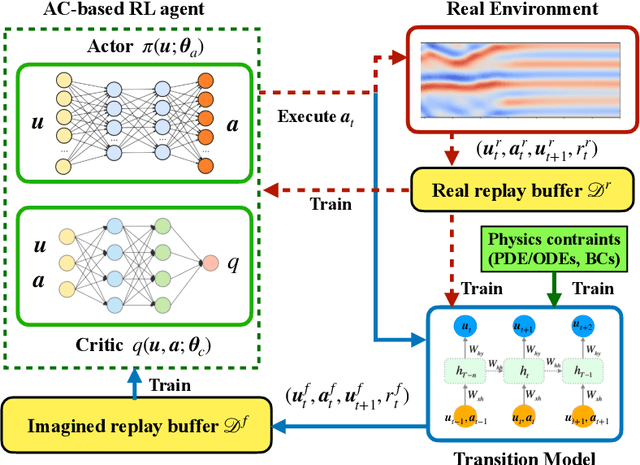

Abstract:Model-based reinforcement learning (MBRL) is believed to have much higher sample efficiency compared to model-free algorithms by learning a predictive model of the environment. However, the performance of MBRL highly relies on the quality of the learned model, which is usually built in a black-box manner and may have poor predictive accuracy outside of the data distribution. The deficiencies of the learned model may prevent the policy from being fully optimized. Although some uncertainty analysis-based remedies have been proposed to alleviate this issue, model bias still poses a great challenge for MBRL. In this work, we propose to leverage the prior knowledge of underlying physics of the environment, where the governing laws are (partially) known. In particular, we developed a physics-informed MBRL framework, where governing equations and physical constraints are utilized to inform the model learning and policy search. By incorporating the prior information of the environment, the quality of the learned model can be notably improved, while the required interactions with the environment are significantly reduced, leading to better sample efficiency and learning performance. The effectiveness and merit have been demonstrated over a handful of classic control problems, where the environments are governed by canonical ordinary/partial differential equations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge