MISCGrasp: Leveraging Multiple Integrated Scales and Contrastive Learning for Enhanced Volumetric Grasping

Robotic grasping faces challenges in adapting to objects with varying shapes and sizes. In this paper, we introduce MISCGrasp, a volumetric grasping method that integrates multi-scale feature extraction with contrastive feature enhancement for self-adaptive grasping. We propose a query-based interaction between high-level and low-level features through the Insight Transformer, while the Empower Transformer selectively attends to the highest-level features, which synergistically strikes a balance between focusing on fine geometric details and overall geometric structures. Furthermore, MISCGrasp utilizes multi-scale contrastive learning to exploit similarities among positive grasp samples, ensuring consistency across multi-scale features. Extensive experiments in both simulated and real-world environments demonstrate that MISCGrasp outperforms baseline and variant methods in tabletop decluttering tasks. More details are available at https://miscgrasp.github.io/.

Steady-State Drifting Equilibrium Analysis of Single-Track Two-Wheeled Robots for Controller Design

Drifting is an advanced driving technique where the wheeled robot's tire-ground interaction breaks the common non-holonomic pure rolling constraint. This allows high-maneuverability tasks like quick cornering, and steady-state drifting control enhances motion stability under lateral slip conditions. While drifting has been successfully achieved in four-wheeled robot systems, its application to single-track two-wheeled (STTW) robots, such as unmanned motorcycles or bicycles, has not been thoroughly studied. To bridge this gap, this paper extends the drifting equilibrium theory to STTW robots and reveals the mechanism behind the steady-state drifting maneuver. Notably, the counter-steering drifting technique used by skilled motorcyclists is explained through this theory. In addition, an analytical algorithm based on intrinsic geometry and kinematics relationships is proposed, reducing the computation time by four orders of magnitude while maintaining less than 6% error compared to numerical methods. Based on equilibrium analysis, a model predictive controller (MPC) is designed to achieve steady-state drifting and equilibrium points transition, with its effectiveness and robustness validated through simulations.

NeuGrasp: Generalizable Neural Surface Reconstruction with Background Priors for Material-Agnostic Object Grasp Detection

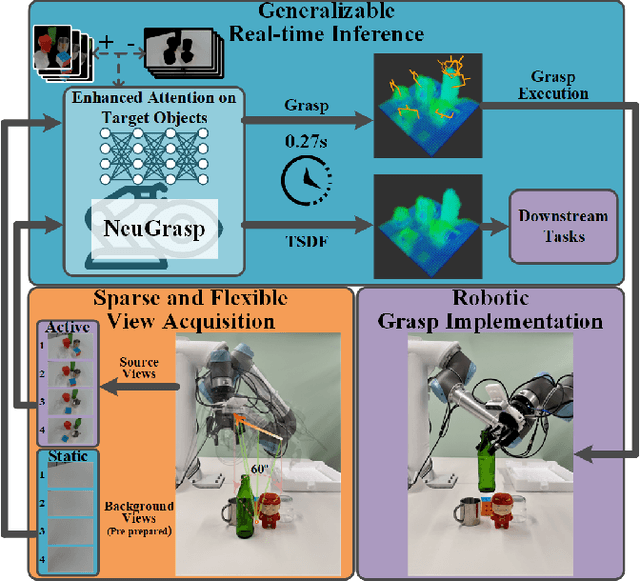
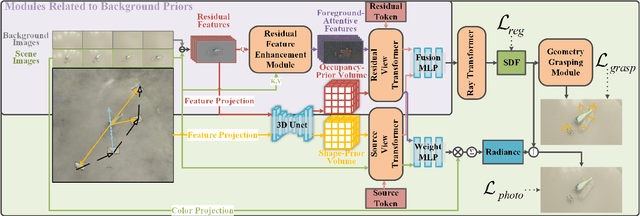
Robotic grasping in scenes with transparent and specular objects presents great challenges for methods relying on accurate depth information. In this paper, we introduce NeuGrasp, a neural surface reconstruction method that leverages background priors for material-agnostic grasp detection. NeuGrasp integrates transformers and global prior volumes to aggregate multi-view features with spatial encoding, enabling robust surface reconstruction in narrow and sparse viewing conditions. By focusing on foreground objects through residual feature enhancement and refining spatial perception with an occupancy-prior volume, NeuGrasp excels in handling objects with transparent and specular surfaces. Extensive experiments in both simulated and real-world scenarios show that NeuGrasp outperforms state-of-the-art methods in grasping while maintaining comparable reconstruction quality. More details are available at https://neugrasp.github.io/.

Predicting path-dependent processes by deep learning

In this paper, we investigate a deep learning method for predicting path-dependent processes based on discretely observed historical information. This method is implemented by considering the prediction as a nonparametric regression and obtaining the regression function through simulated samples and deep neural networks. When applying this method to fractional Brownian motion and the solutions of some stochastic differential equations driven by it, we theoretically proved that the $L_2$ errors converge to 0, and we further discussed the scope of the method. With the frequency of discrete observations tending to infinity, the predictions based on discrete observations converge to the predictions based on continuous observations, which implies that we can make approximations by the method. We apply the method to the fractional Brownian motion and the fractional Ornstein-Uhlenbeck process as examples. Comparing the results with the theoretical optimal predictions and taking the mean square error as a measure, the numerical simulations demonstrate that the method can generate accurate results. We also analyze the impact of factors such as prediction period, Hurst index, etc. on the accuracy.

Asynchronous Parallel Reinforcement Learning for Optimizing Propulsive Performance in Fin Ray Control

Fish fin rays constitute a sophisticated control system for ray-finned fish, facilitating versatile locomotion within complex fluid environments. Despite extensive research on the kinematics and hydrodynamics of fish locomotion, the intricate control strategies in fin-ray actuation remain largely unexplored. While deep reinforcement learning (DRL) has demonstrated potential in managing complex nonlinear dynamics; its trial-and-error nature limits its application to problems involving computationally demanding environmental interactions. This study introduces a cutting-edge off-policy DRL algorithm, interacting with a fluid-structure interaction (FSI) environment to acquire intricate fin-ray control strategies tailored for various propulsive performance objectives. To enhance training efficiency and enable scalable parallelism, an innovative asynchronous parallel training (APT) strategy is proposed, which fully decouples FSI environment interactions and policy/value network optimization. The results demonstrated the success of the proposed method in discovering optimal complex policies for fin-ray actuation control, resulting in a superior propulsive performance compared to the optimal sinusoidal actuation function identified through a parametric grid search. The merit and effectiveness of the APT approach are also showcased through comprehensive comparison with conventional DRL training strategies in numerical experiments of controlling nonlinear dynamics.