Multi-fidelity Reinforcement Learning Control for Complex Dynamical Systems

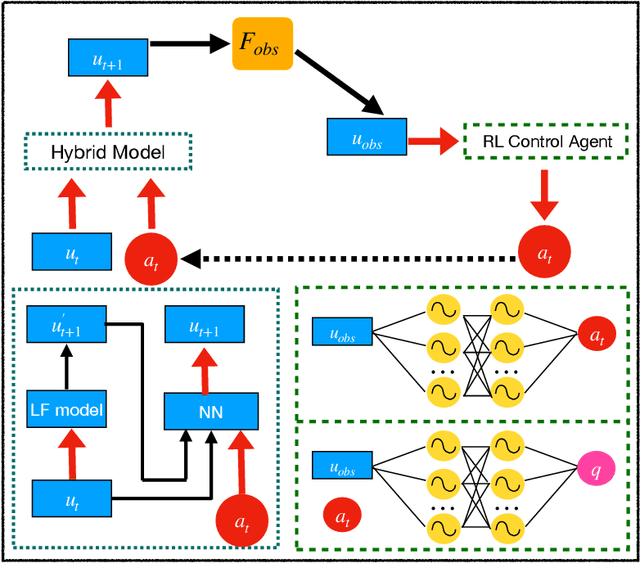
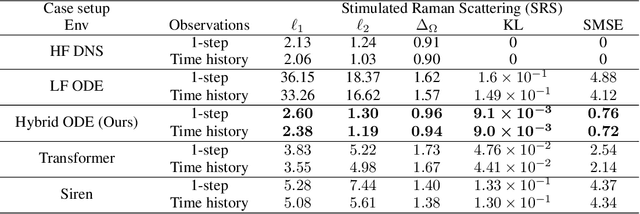
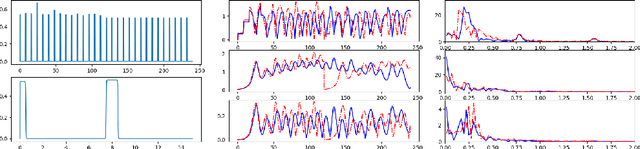
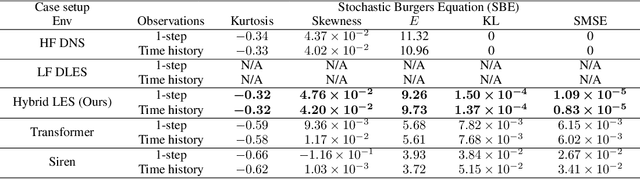
Controlling instabilities in complex dynamical systems is challenging in scientific and engineering applications. Deep reinforcement learning (DRL) has seen promising results for applications in different scientific applications. The many-query nature of control tasks requires multiple interactions with real environments of the underlying physics. However, it is usually sparse to collect from the experiments or expensive to simulate for complex dynamics. Alternatively, controlling surrogate modeling could mitigate the computational cost issue. However, a fast and accurate learning-based model by offline training makes it very hard to get accurate pointwise dynamics when the dynamics are chaotic. To bridge this gap, the current work proposes a multi-fidelity reinforcement learning (MFRL) framework that leverages differentiable hybrid models for control tasks, where a physics-based hybrid model is corrected by limited high-fidelity data. We also proposed a spectrum-based reward function for RL learning. The effect of the proposed framework is demonstrated on two complex dynamics in physics. The statistics of the MFRL control result match that computed from many-query evaluations of the high-fidelity environments and outperform other SOTA baselines.

Implicit Neural Differential Model for Spatiotemporal Dynamics

Hybrid neural-physics modeling frameworks through differentiable programming have emerged as powerful tools in scientific machine learning, enabling the integration of known physics with data-driven learning to improve prediction accuracy and generalizability. However, most existing hybrid frameworks rely on explicit recurrent formulations, which suffer from numerical instability and error accumulation during long-horizon forecasting. In this work, we introduce Im-PiNDiff, a novel implicit physics-integrated neural differentiable solver for stable and accurate modeling of spatiotemporal dynamics. Inspired by deep equilibrium models, Im-PiNDiff advances the state using implicit fixed-point layers, enabling robust long-term simulation while remaining fully end-to-end differentiable. To enable scalable training, we introduce a hybrid gradient propagation strategy that integrates adjoint-state methods with reverse-mode automatic differentiation. This approach eliminates the need to store intermediate solver states and decouples memory complexity from the number of solver iterations, significantly reducing training overhead. We further incorporate checkpointing techniques to manage memory in long-horizon rollouts. Numerical experiments on various spatiotemporal PDE systems, including advection-diffusion processes, Burgers' dynamics, and multi-physics chemical vapor infiltration processes, demonstrate that Im-PiNDiff achieves superior predictive performance, enhanced numerical stability, and substantial reductions in memory and runtime cost relative to explicit and naive implicit baselines. This work provides a principled, efficient, and scalable framework for hybrid neural-physics modeling.

AI-Powered Automated Model Construction for Patient-Specific CFD Simulations of Aortic Flows

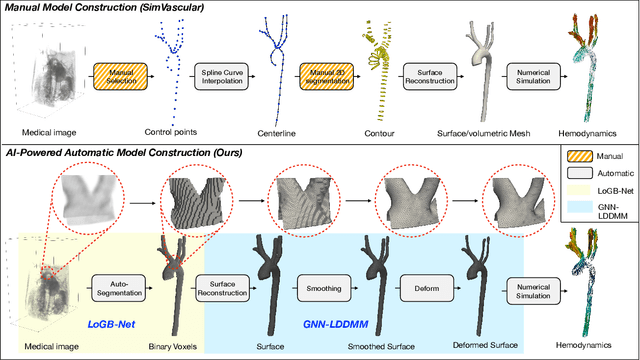
Image-based modeling is essential for understanding cardiovascular hemodynamics and advancing the diagnosis and treatment of cardiovascular diseases. Constructing patient-specific vascular models remains labor-intensive, error-prone, and time-consuming, limiting their clinical applications. This study introduces a deep-learning framework that automates the creation of simulation-ready vascular models from medical images. The framework integrates a segmentation module for accurate voxel-based vessel delineation with a surface deformation module that performs anatomically consistent and unsupervised surface refinements guided by medical image data. By unifying voxel segmentation and surface deformation into a single cohesive pipeline, the framework addresses key limitations of existing methods, enhancing geometric accuracy and computational efficiency. Evaluated on publicly available datasets, the proposed approach demonstrates state-of-the-art performance in segmentation and mesh quality while significantly reducing manual effort and processing time. This work advances the scalability and reliability of image-based computational modeling, facilitating broader applications in clinical and research settings.

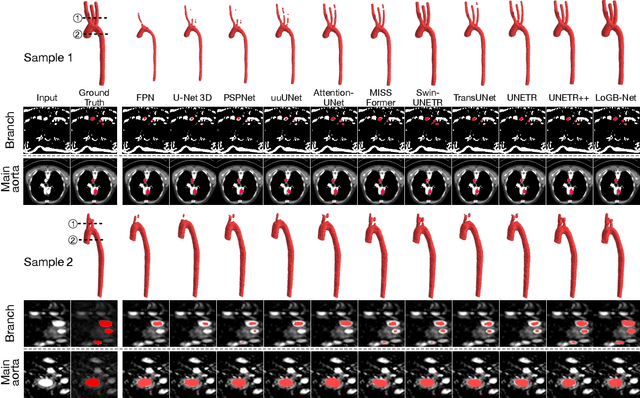
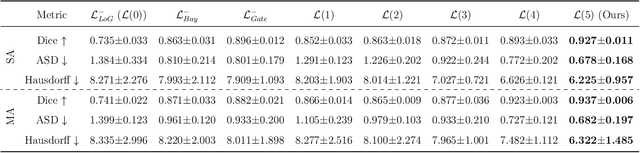
Hierarchical LoG Bayesian Neural Network for Enhanced Aorta Segmentation

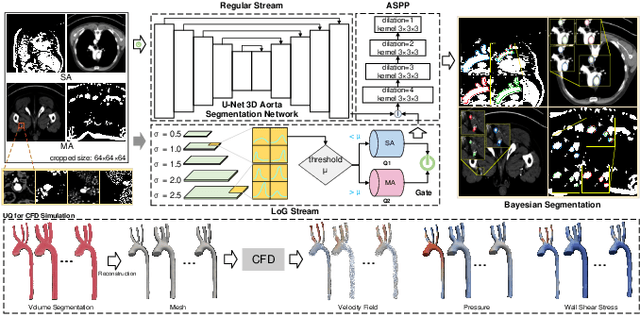
Accurate segmentation of the aorta and its associated arch branches is crucial for diagnosing aortic diseases. While deep learning techniques have significantly improved aorta segmentation, they remain challenging due to the intricate multiscale structure and the complexity of the surrounding tissues. This paper presents a novel approach for enhancing aorta segmentation using a Bayesian neural network-based hierarchical Laplacian of Gaussian (LoG) model. Our model consists of a 3D U-Net stream and a hierarchical LoG stream: the former provides an initial aorta segmentation, and the latter enhances blood vessel detection across varying scales by learning suitable LoG kernels, enabling self-adaptive handling of different parts of the aorta vessels with significant scale differences. We employ a Bayesian method to parameterize the LoG stream and provide confidence intervals for the segmentation results, ensuring robustness and reliability of the prediction for vascular medical image analysts. Experimental results show that our model can accurately segment main and supra-aortic vessels, yielding at least a 3% gain in the Dice coefficient over state-of-the-art methods across multiple volumes drawn from two aorta datasets, and can provide reliable confidence intervals for different parts of the aorta. The code is available at https://github.com/adlsn/LoGBNet.

CoNFiLD-inlet: Synthetic Turbulence Inflow Using Generative Latent Diffusion Models with Neural Fields

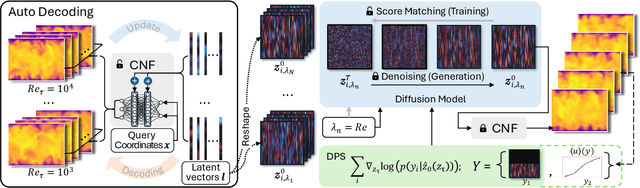
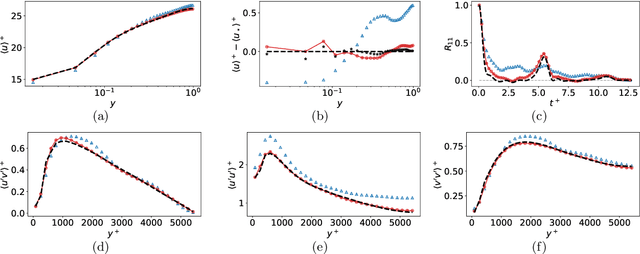
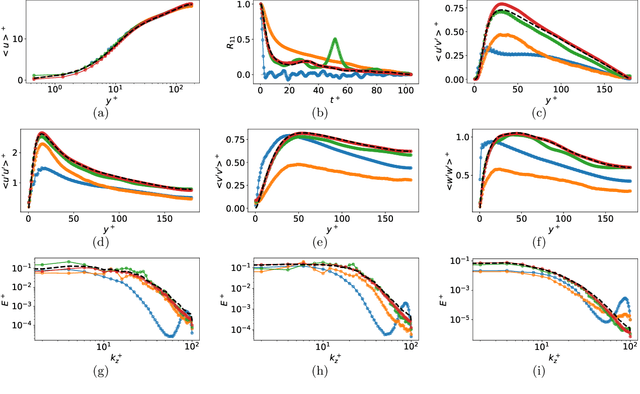
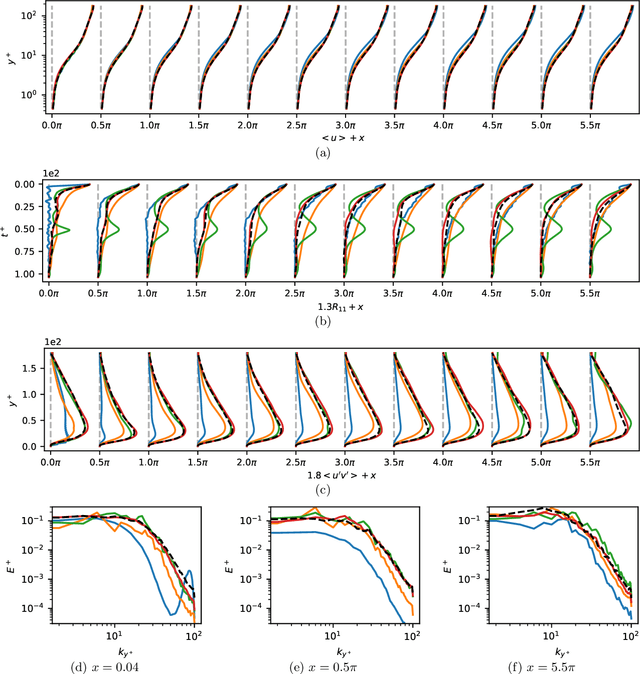
Eddy-resolving turbulence simulations require stochastic inflow conditions that accurately replicate the complex, multi-scale structures of turbulence. Traditional recycling-based methods rely on computationally expensive precursor simulations, while existing synthetic inflow generators often fail to reproduce realistic coherent structures of turbulence. Recent advances in deep learning (DL) have opened new possibilities for inflow turbulence generation, yet many DL-based methods rely on deterministic, autoregressive frameworks prone to error accumulation, resulting in poor robustness for long-term predictions. In this work, we present CoNFiLD-inlet, a novel DL-based inflow turbulence generator that integrates diffusion models with a conditional neural field (CNF)-encoded latent space to produce realistic, stochastic inflow turbulence. By parameterizing inflow conditions using Reynolds numbers, CoNFiLD-inlet generalizes effectively across a wide range of Reynolds numbers ($Re_\tau$ between $10^3$ and $10^4$) without requiring retraining or parameter tuning. Comprehensive validation through a priori and a posteriori tests in Direct Numerical Simulation (DNS) and Wall-Modeled Large Eddy Simulation (WMLES) demonstrates its high fidelity, robustness, and scalability, positioning it as an efficient and versatile solution for inflow turbulence synthesis.

P$^2$C$^2$Net: PDE-Preserved Coarse Correction Network for efficient prediction of spatiotemporal dynamics

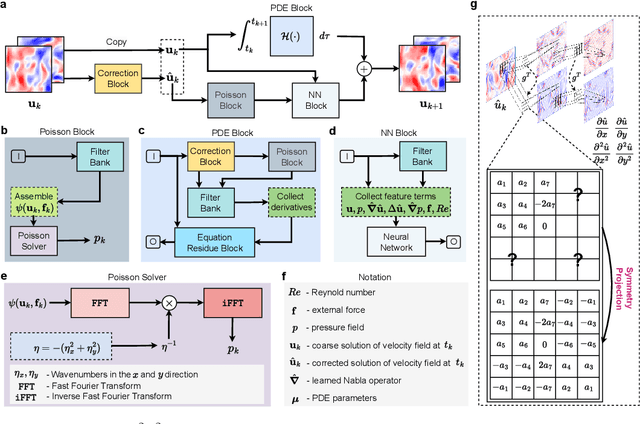
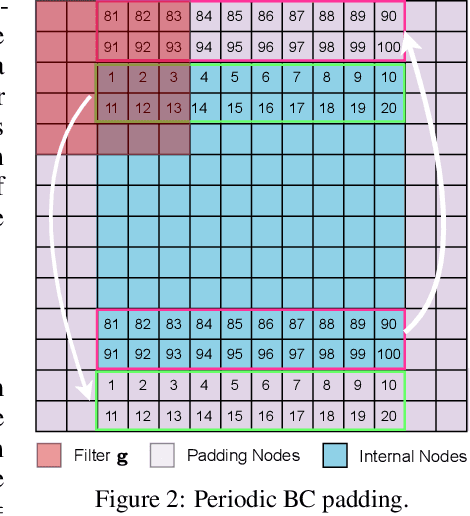
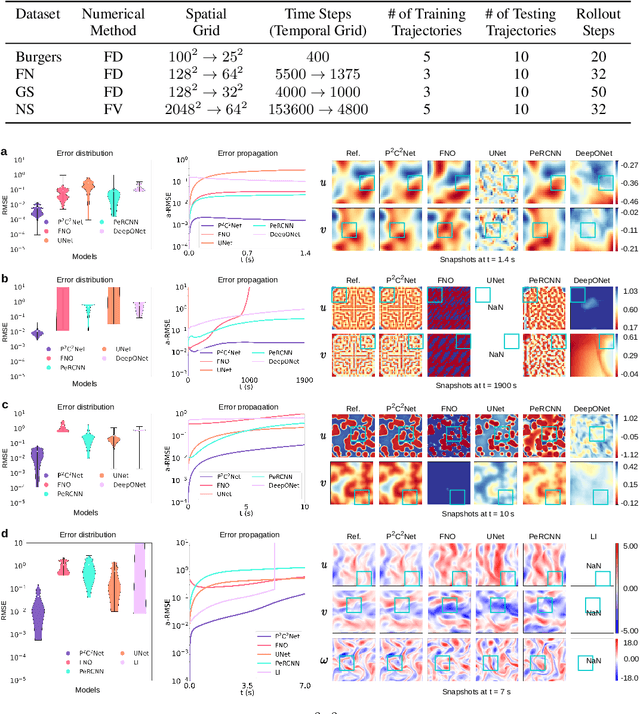
When solving partial differential equations (PDEs), classical numerical methods often require fine mesh grids and small time stepping to meet stability, consistency, and convergence conditions, leading to high computational cost. Recently, machine learning has been increasingly utilized to solve PDE problems, but they often encounter challenges related to interpretability, generalizability, and strong dependency on rich labeled data. Hence, we introduce a new PDE-Preserved Coarse Correction Network (P$^2$C$^2$Net) to efficiently solve spatiotemporal PDE problems on coarse mesh grids in small data regimes. The model consists of two synergistic modules: (1) a trainable PDE block that learns to update the coarse solution (i.e., the system state), based on a high-order numerical scheme with boundary condition encoding, and (2) a neural network block that consistently corrects the solution on the fly. In particular, we propose a learnable symmetric Conv filter, with weights shared over the entire model, to accurately estimate the spatial derivatives of PDE based on the neural-corrected system state. The resulting physics-encoded model is capable of handling limited training data (e.g., 3--5 trajectories) and accelerates the prediction of PDE solutions on coarse spatiotemporal grids while maintaining a high accuracy. P$^2$C$^2$Net achieves consistent state-of-the-art performance with over 50\% gain (e.g., in terms of relative prediction error) across four datasets covering complex reaction-diffusion processes and turbulent flows.

Asynchronous Parallel Reinforcement Learning for Optimizing Propulsive Performance in Fin Ray Control

Fish fin rays constitute a sophisticated control system for ray-finned fish, facilitating versatile locomotion within complex fluid environments. Despite extensive research on the kinematics and hydrodynamics of fish locomotion, the intricate control strategies in fin-ray actuation remain largely unexplored. While deep reinforcement learning (DRL) has demonstrated potential in managing complex nonlinear dynamics; its trial-and-error nature limits its application to problems involving computationally demanding environmental interactions. This study introduces a cutting-edge off-policy DRL algorithm, interacting with a fluid-structure interaction (FSI) environment to acquire intricate fin-ray control strategies tailored for various propulsive performance objectives. To enhance training efficiency and enable scalable parallelism, an innovative asynchronous parallel training (APT) strategy is proposed, which fully decouples FSI environment interactions and policy/value network optimization. The results demonstrated the success of the proposed method in discovering optimal complex policies for fin-ray actuation control, resulting in a superior propulsive performance compared to the optimal sinusoidal actuation function identified through a parametric grid search. The merit and effectiveness of the APT approach are also showcased through comprehensive comparison with conventional DRL training strategies in numerical experiments of controlling nonlinear dynamics.

DiffHybrid-UQ: Uncertainty Quantification for Differentiable Hybrid Neural Modeling

The hybrid neural differentiable models mark a significant advancement in the field of scientific machine learning. These models, integrating numerical representations of known physics into deep neural networks, offer enhanced predictive capabilities and show great potential for data-driven modeling of complex physical systems. However, a critical and yet unaddressed challenge lies in the quantification of inherent uncertainties stemming from multiple sources. Addressing this gap, we introduce a novel method, DiffHybrid-UQ, for effective and efficient uncertainty propagation and estimation in hybrid neural differentiable models, leveraging the strengths of deep ensemble Bayesian learning and nonlinear transformations. Specifically, our approach effectively discerns and quantifies both aleatoric uncertainties, arising from data noise, and epistemic uncertainties, resulting from model-form discrepancies and data sparsity. This is achieved within a Bayesian model averaging framework, where aleatoric uncertainties are modeled through hybrid neural models. The unscented transformation plays a pivotal role in enabling the flow of these uncertainties through the nonlinear functions within the hybrid model. In contrast, epistemic uncertainties are estimated using an ensemble of stochastic gradient descent (SGD) trajectories. This approach offers a practical approximation to the posterior distribution of both the network parameters and the physical parameters. Notably, the DiffHybrid-UQ framework is designed for simplicity in implementation and high scalability, making it suitable for parallel computing environments. The merits of the proposed method have been demonstrated through problems governed by both ordinary and partial differentiable equations.

Bayesian Conditional Diffusion Models for Versatile Spatiotemporal Turbulence Generation

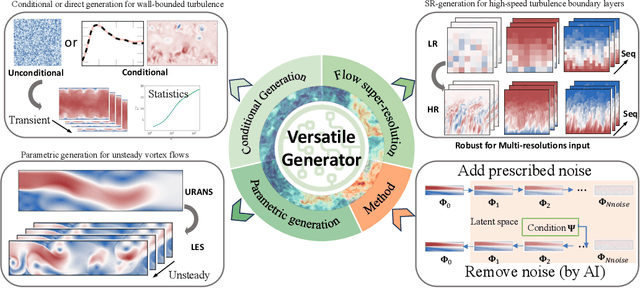
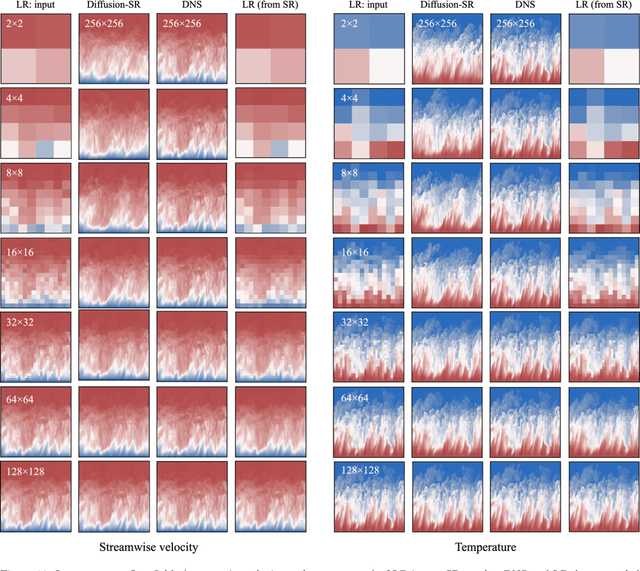
Turbulent flows have historically presented formidable challenges to predictive computational modeling. Traditional numerical simulations often require vast computational resources, making them infeasible for numerous engineering applications. As an alternative, deep learning-based surrogate models have emerged, offering data-drive solutions. However, these are typically constructed within deterministic settings, leading to shortfall in capturing the innate chaotic and stochastic behaviors of turbulent dynamics. We introduce a novel generative framework grounded in probabilistic diffusion models for versatile generation of spatiotemporal turbulence. Our method unifies both unconditional and conditional sampling strategies within a Bayesian framework, which can accommodate diverse conditioning scenarios, including those with a direct differentiable link between specified conditions and generated unsteady flow outcomes, and scenarios lacking such explicit correlations. A notable feature of our approach is the method proposed for long-span flow sequence generation, which is based on autoregressive gradient-based conditional sampling, eliminating the need for cumbersome retraining processes. We showcase the versatile turbulence generation capability of our framework through a suite of numerical experiments, including: 1) the synthesis of LES simulated instantaneous flow sequences from URANS inputs; 2) holistic generation of inhomogeneous, anisotropic wall-bounded turbulence, whether from given initial conditions, prescribed turbulence statistics, or entirely from scratch; 3) super-resolved generation of high-speed turbulent boundary layer flows from low-resolution data across a range of input resolutions. Collectively, our numerical experiments highlight the merit and transformative potential of the proposed methods, making a significant advance in the field of turbulence generation.

Probabilistic Physics-integrated Neural Differentiable Modeling for Isothermal Chemical Vapor Infiltration Process

Chemical vapor infiltration (CVI) is a widely adopted manufacturing technique used in producing carbon-carbon and carbon-silicon carbide composites. These materials are especially valued in the aerospace and automotive industries for their robust strength and lightweight characteristics. The densification process during CVI critically influences the final performance, quality, and consistency of these composite materials. Experimentally optimizing the CVI processes is challenging due to long experimental time and large optimization space. To address these challenges, this work takes a modeling-centric approach. Due to the complexities and limited experimental data of the isothermal CVI densification process, we have developed a data-driven predictive model using the physics-integrated neural differentiable (PiNDiff) modeling framework. An uncertainty quantification feature has been embedded within the PiNDiff method, bolstering the model's reliability and robustness. Through comprehensive numerical experiments involving both synthetic and real-world manufacturing data, the proposed method showcases its capability in modeling densification during the CVI process. This research highlights the potential of the PiNDiff framework as an instrumental tool for advancing our understanding, simulation, and optimization of the CVI manufacturing process, particularly when faced with sparse data and an incomplete description of the underlying physics.