CoNFiLD-inlet: Synthetic Turbulence Inflow Using Generative Latent Diffusion Models with Neural Fields

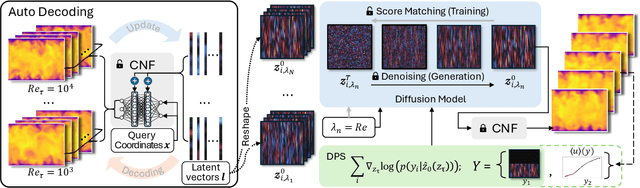
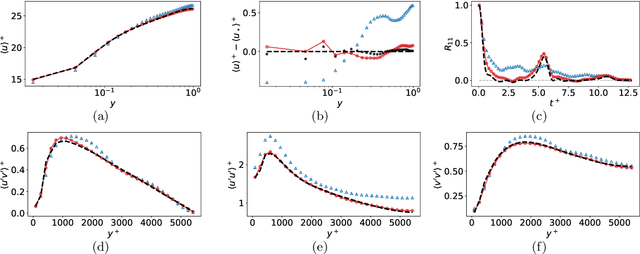
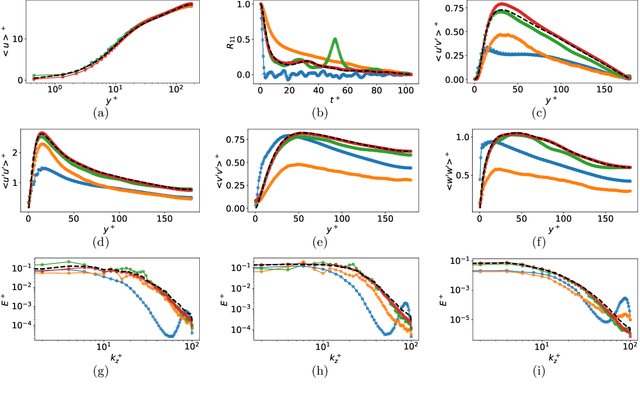
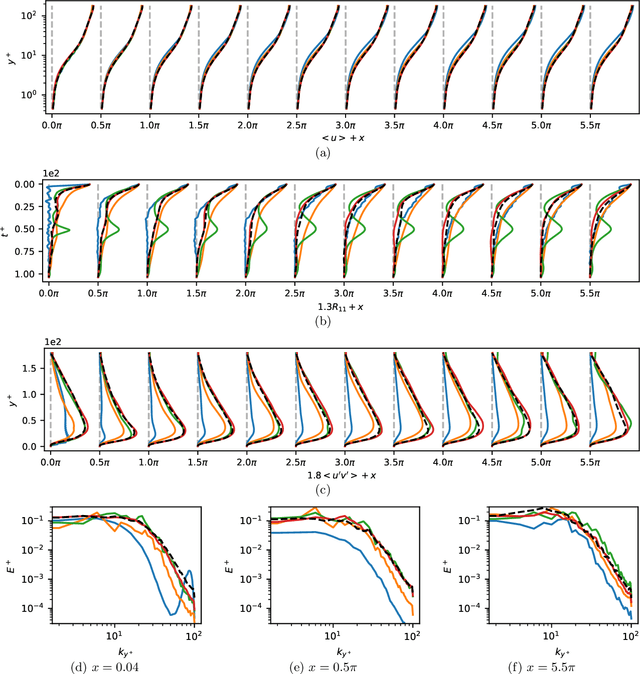
Eddy-resolving turbulence simulations require stochastic inflow conditions that accurately replicate the complex, multi-scale structures of turbulence. Traditional recycling-based methods rely on computationally expensive precursor simulations, while existing synthetic inflow generators often fail to reproduce realistic coherent structures of turbulence. Recent advances in deep learning (DL) have opened new possibilities for inflow turbulence generation, yet many DL-based methods rely on deterministic, autoregressive frameworks prone to error accumulation, resulting in poor robustness for long-term predictions. In this work, we present CoNFiLD-inlet, a novel DL-based inflow turbulence generator that integrates diffusion models with a conditional neural field (CNF)-encoded latent space to produce realistic, stochastic inflow turbulence. By parameterizing inflow conditions using Reynolds numbers, CoNFiLD-inlet generalizes effectively across a wide range of Reynolds numbers ($Re_\tau$ between $10^3$ and $10^4$) without requiring retraining or parameter tuning. Comprehensive validation through a priori and a posteriori tests in Direct Numerical Simulation (DNS) and Wall-Modeled Large Eddy Simulation (WMLES) demonstrates its high fidelity, robustness, and scalability, positioning it as an efficient and versatile solution for inflow turbulence synthesis.

Bayesian Conditional Diffusion Models for Versatile Spatiotemporal Turbulence Generation

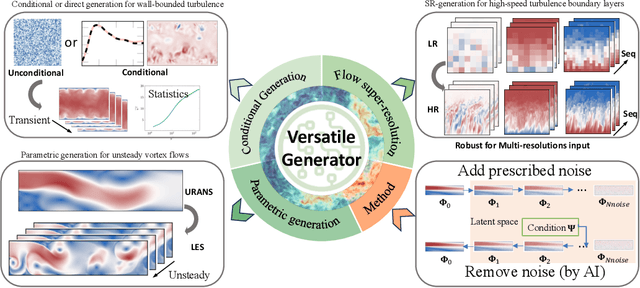
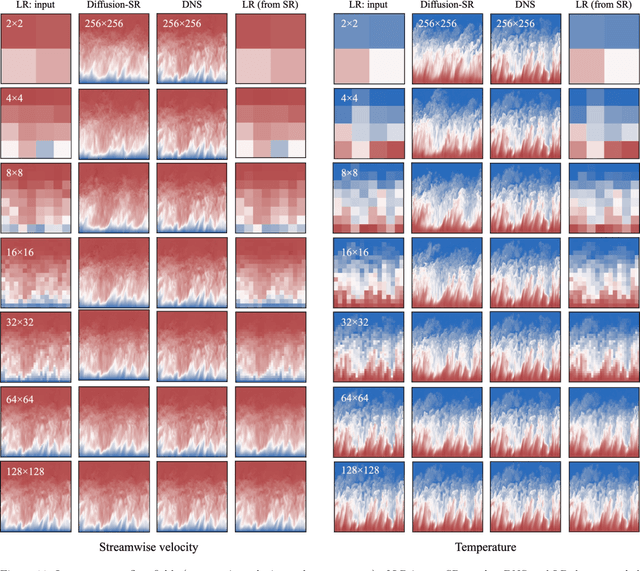
Turbulent flows have historically presented formidable challenges to predictive computational modeling. Traditional numerical simulations often require vast computational resources, making them infeasible for numerous engineering applications. As an alternative, deep learning-based surrogate models have emerged, offering data-drive solutions. However, these are typically constructed within deterministic settings, leading to shortfall in capturing the innate chaotic and stochastic behaviors of turbulent dynamics. We introduce a novel generative framework grounded in probabilistic diffusion models for versatile generation of spatiotemporal turbulence. Our method unifies both unconditional and conditional sampling strategies within a Bayesian framework, which can accommodate diverse conditioning scenarios, including those with a direct differentiable link between specified conditions and generated unsteady flow outcomes, and scenarios lacking such explicit correlations. A notable feature of our approach is the method proposed for long-span flow sequence generation, which is based on autoregressive gradient-based conditional sampling, eliminating the need for cumbersome retraining processes. We showcase the versatile turbulence generation capability of our framework through a suite of numerical experiments, including: 1) the synthesis of LES simulated instantaneous flow sequences from URANS inputs; 2) holistic generation of inhomogeneous, anisotropic wall-bounded turbulence, whether from given initial conditions, prescribed turbulence statistics, or entirely from scratch; 3) super-resolved generation of high-speed turbulent boundary layer flows from low-resolution data across a range of input resolutions. Collectively, our numerical experiments highlight the merit and transformative potential of the proposed methods, making a significant advance in the field of turbulence generation.