P$^2$C$^2$Net: PDE-Preserved Coarse Correction Network for efficient prediction of spatiotemporal dynamics

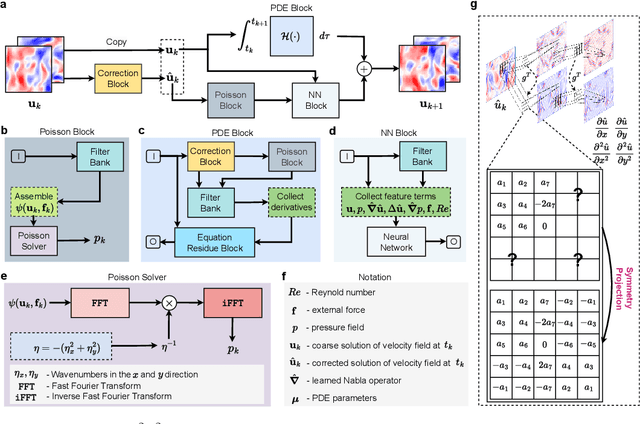
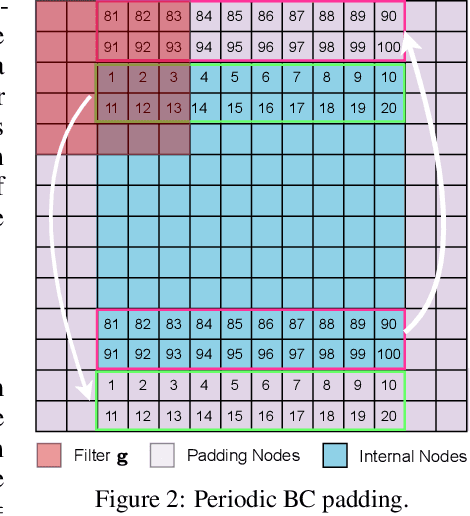
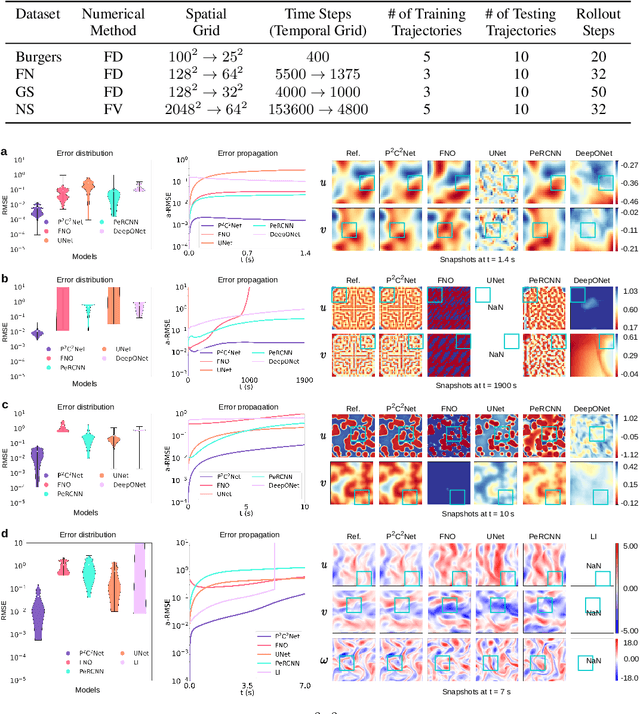
When solving partial differential equations (PDEs), classical numerical methods often require fine mesh grids and small time stepping to meet stability, consistency, and convergence conditions, leading to high computational cost. Recently, machine learning has been increasingly utilized to solve PDE problems, but they often encounter challenges related to interpretability, generalizability, and strong dependency on rich labeled data. Hence, we introduce a new PDE-Preserved Coarse Correction Network (P$^2$C$^2$Net) to efficiently solve spatiotemporal PDE problems on coarse mesh grids in small data regimes. The model consists of two synergistic modules: (1) a trainable PDE block that learns to update the coarse solution (i.e., the system state), based on a high-order numerical scheme with boundary condition encoding, and (2) a neural network block that consistently corrects the solution on the fly. In particular, we propose a learnable symmetric Conv filter, with weights shared over the entire model, to accurately estimate the spatial derivatives of PDE based on the neural-corrected system state. The resulting physics-encoded model is capable of handling limited training data (e.g., 3--5 trajectories) and accelerates the prediction of PDE solutions on coarse spatiotemporal grids while maintaining a high accuracy. P$^2$C$^2$Net achieves consistent state-of-the-art performance with over 50\% gain (e.g., in terms of relative prediction error) across four datasets covering complex reaction-diffusion processes and turbulent flows.

PhyMPGN: Physics-encoded Message Passing Graph Network for spatiotemporal PDE systems

Solving partial differential equations (PDEs) serves as a cornerstone for modeling complex dynamical systems. Recent progresses have demonstrated grand benefits of data-driven neural-based models for predicting spatiotemporal dynamics (e.g., tremendous speedup gain compared with classical numerical methods). However, most existing neural models rely on rich training data, have limited extrapolation and generalization abilities, and suffer to produce precise or reliable physical prediction under intricate conditions (e.g., irregular mesh or geometry, complex boundary conditions, diverse PDE parameters, etc.). To this end, we propose a new graph learning approach, namely, Physics-encoded Message Passing Graph Network (PhyMPGN), to model spatiotemporal PDE systems on irregular meshes given small training datasets. Specifically, we incorporate a GNN into a numerical integrator to approximate the temporal marching of spatiotemporal dynamics for a given PDE system. Considering that many physical phenomena are governed by diffusion processes, we further design a learnable Laplace block, which encodes the discrete Laplace-Beltrami operator, to aid and guide the GNN learning in a physically feasible solution space. A boundary condition padding strategy is also designed to improve the model convergence and accuracy. Extensive experiments demonstrate that PhyMPGN is capable of accurately predicting various types of spatiotemporal dynamics on coarse unstructured meshes, consistently achieves the state-of-the-art results, and outperforms other baselines with considerable gains.

Learning to simulate partially known spatio-temporal dynamics with trainable difference operators

Recently, using neural networks to simulate spatio-temporal dynamics has received a lot of attention. However, most existing methods adopt pure data-driven black-box models, which have limited accuracy and interpretability. By combining trainable difference operators with black-box models, we propose a new hybrid architecture explicitly embedded with partial prior knowledge of the underlying PDEs named PDE-Net++. Furthermore, we introduce two distinct options called the trainable flipping difference layer (TFDL) and the trainable dynamic difference layer (TDDL) for the difference operators. Numerous numerical experiments have demonstrated that PDE-Net++ has superior prediction accuracy and better extrapolation performance than black-box models.

Meta-Auto-Decoder for Solving Parametric Partial Differential Equations

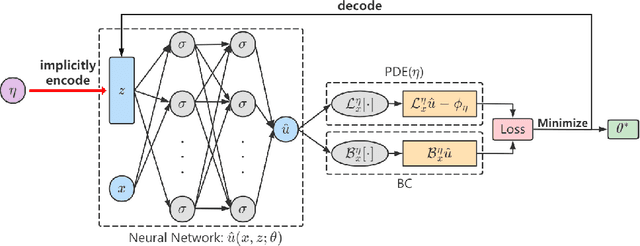
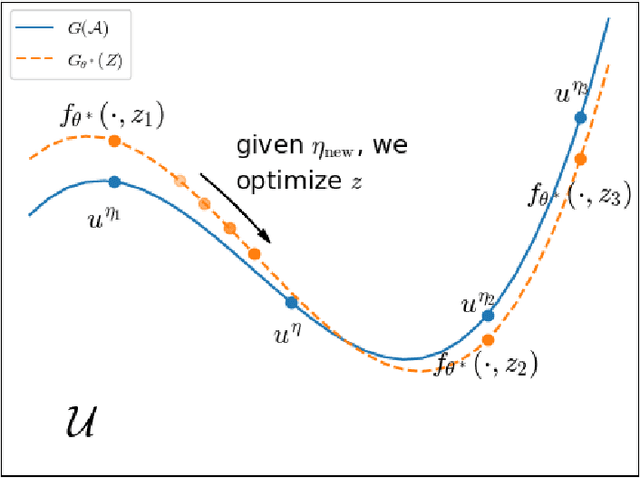
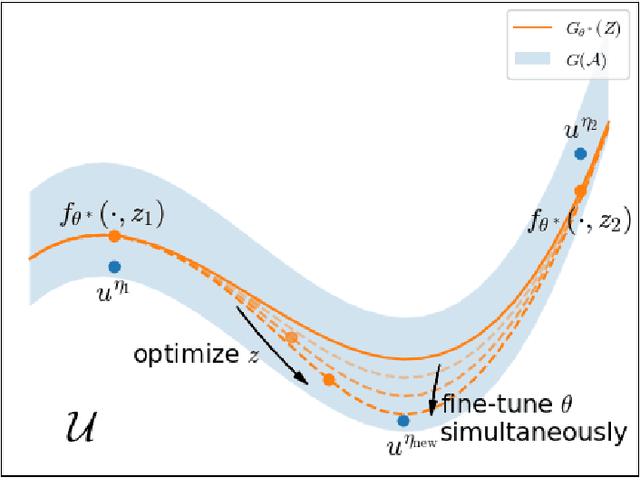
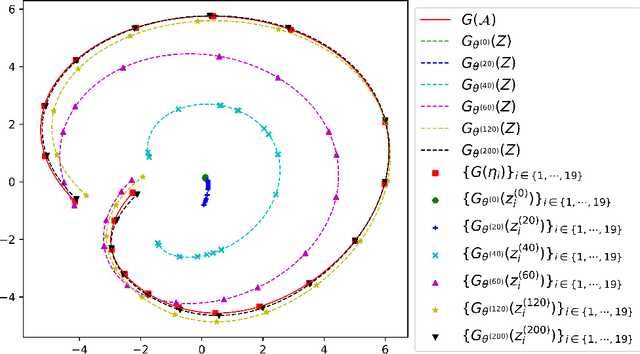
Partial Differential Equations (PDEs) are ubiquitous in many disciplines of science and engineering and notoriously difficult to solve. In general, closed-form solutions of PDEs are unavailable and numerical approximation methods are computationally expensive. The parameters of PDEs are variable in many applications, such as inverse problems, control and optimization, risk assessment, and uncertainty quantification. In these applications, our goal is to solve parametric PDEs rather than one instance of them. Our proposed approach, called Meta-Auto-Decoder (MAD), treats solving parametric PDEs as a meta-learning problem and utilizes the Auto-Decoder structure in \cite{park2019deepsdf} to deal with different tasks/PDEs. Physics-informed losses induced from the PDE governing equations and boundary conditions is used as the training losses for different tasks. The goal of MAD is to learn a good model initialization that can generalize across different tasks, and eventually enables the unseen task to be learned faster. The inspiration of MAD comes from (conjectured) low-dimensional structure of parametric PDE solutions and we explain our approach from the perspective of manifold learning. Finally, we demonstrate the power of MAD though extensive numerical studies, including Burgers' equation, Laplace's equation and time-domain Maxwell's equations. MAD exhibits faster convergence speed without losing the accuracy compared with other deep learning methods.

Solving Partial Differential Equations with Point Source Based on Physics-Informed Neural Networks

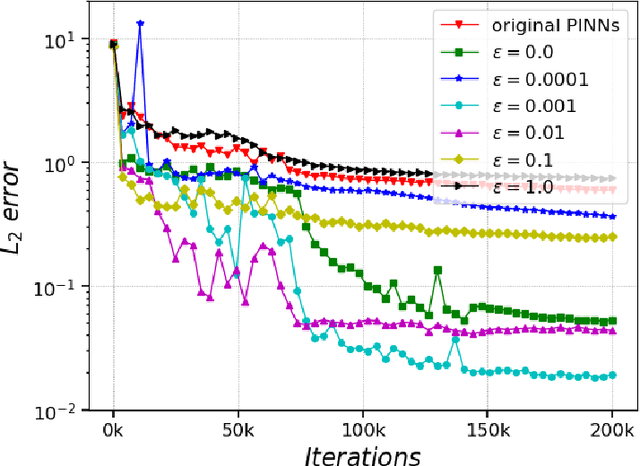
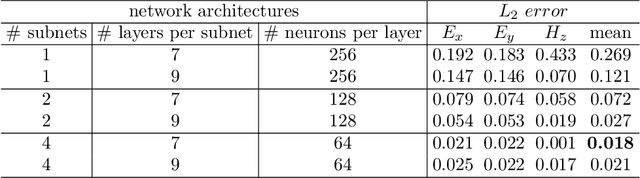
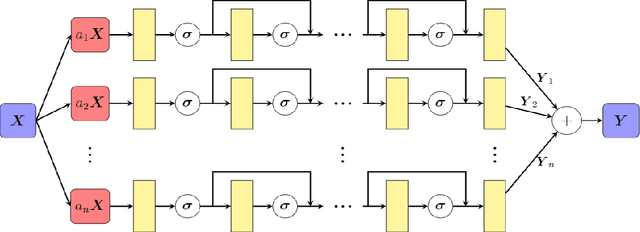
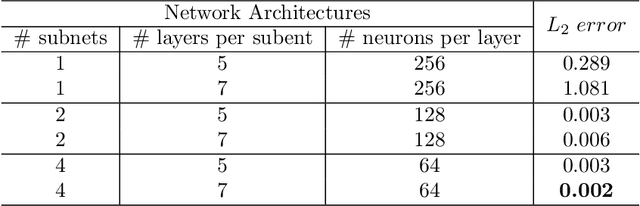
In recent years, deep learning technology has been used to solve partial differential equations (PDEs), among which the physics-informed neural networks (PINNs) emerges to be a promising method for solving both forward and inverse PDE problems. PDEs with a point source that is expressed as a Dirac delta function in the governing equations are mathematical models of many physical processes. However, they cannot be solved directly by conventional PINNs method due to the singularity brought by the Dirac delta function. We propose a universal solution to tackle this problem with three novel techniques. Firstly the Dirac delta function is modeled as a continuous probability density function to eliminate the singularity; secondly a lower bound constrained uncertainty weighting algorithm is proposed to balance the PINNs losses between point source area and other areas; and thirdly a multi-scale deep neural network with periodic activation function is used to improve the accuracy and convergence speed of the PINNs method. We evaluate the proposed method with three representative PDEs, and the experimental results show that our method outperforms existing deep learning-based methods with respect to the accuracy, the efficiency and the versatility.