Beiji Shi
Meta-Auto-Decoder for Solving Parametric Partial Differential Equations
Nov 15, 2021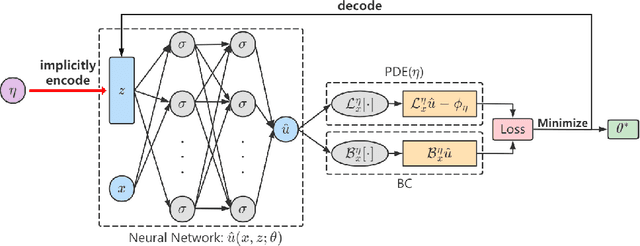
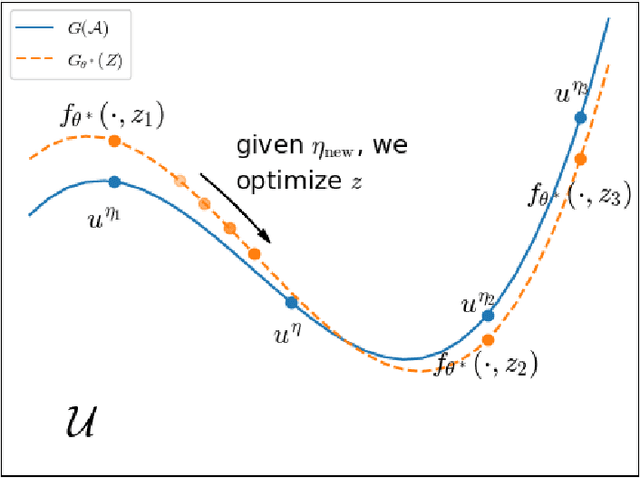
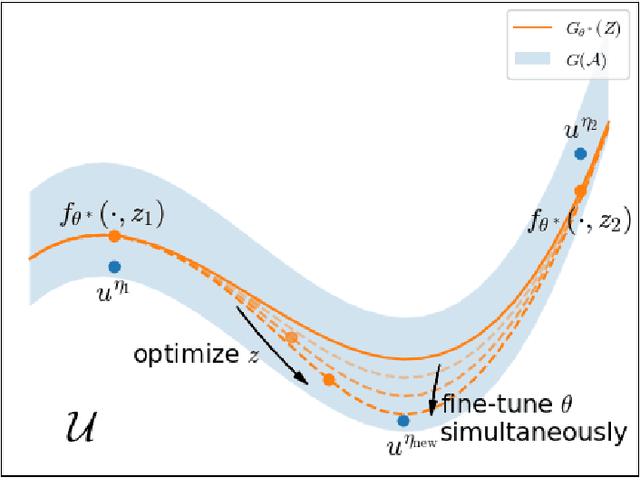
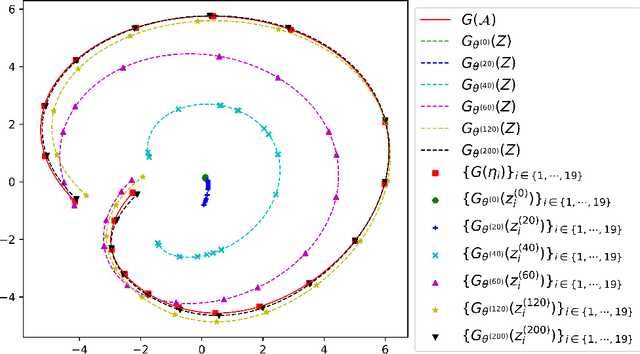
Abstract:Partial Differential Equations (PDEs) are ubiquitous in many disciplines of science and engineering and notoriously difficult to solve. In general, closed-form solutions of PDEs are unavailable and numerical approximation methods are computationally expensive. The parameters of PDEs are variable in many applications, such as inverse problems, control and optimization, risk assessment, and uncertainty quantification. In these applications, our goal is to solve parametric PDEs rather than one instance of them. Our proposed approach, called Meta-Auto-Decoder (MAD), treats solving parametric PDEs as a meta-learning problem and utilizes the Auto-Decoder structure in \cite{park2019deepsdf} to deal with different tasks/PDEs. Physics-informed losses induced from the PDE governing equations and boundary conditions is used as the training losses for different tasks. The goal of MAD is to learn a good model initialization that can generalize across different tasks, and eventually enables the unseen task to be learned faster. The inspiration of MAD comes from (conjectured) low-dimensional structure of parametric PDE solutions and we explain our approach from the perspective of manifold learning. Finally, we demonstrate the power of MAD though extensive numerical studies, including Burgers' equation, Laplace's equation and time-domain Maxwell's equations. MAD exhibits faster convergence speed without losing the accuracy compared with other deep learning methods.
Solving Partial Differential Equations with Point Source Based on Physics-Informed Neural Networks
Nov 02, 2021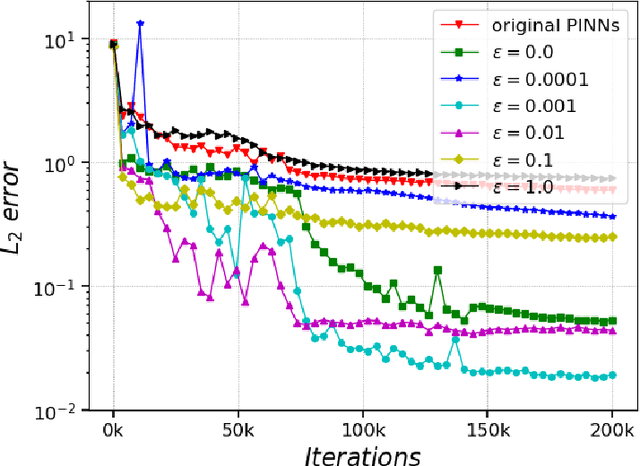
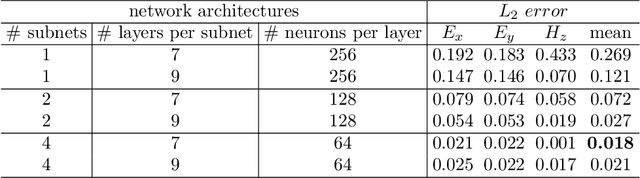
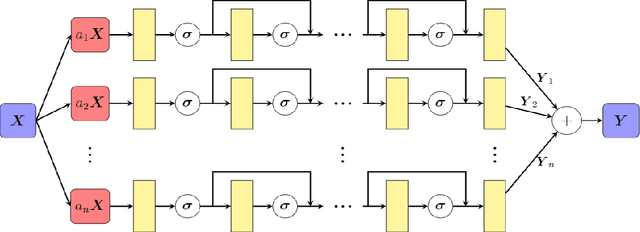
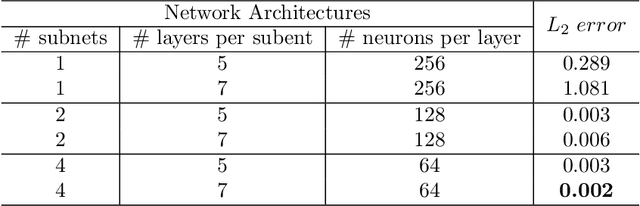
Abstract:In recent years, deep learning technology has been used to solve partial differential equations (PDEs), among which the physics-informed neural networks (PINNs) emerges to be a promising method for solving both forward and inverse PDE problems. PDEs with a point source that is expressed as a Dirac delta function in the governing equations are mathematical models of many physical processes. However, they cannot be solved directly by conventional PINNs method due to the singularity brought by the Dirac delta function. We propose a universal solution to tackle this problem with three novel techniques. Firstly the Dirac delta function is modeled as a continuous probability density function to eliminate the singularity; secondly a lower bound constrained uncertainty weighting algorithm is proposed to balance the PINNs losses between point source area and other areas; and thirdly a multi-scale deep neural network with periodic activation function is used to improve the accuracy and convergence speed of the PINNs method. We evaluate the proposed method with three representative PDEs, and the experimental results show that our method outperforms existing deep learning-based methods with respect to the accuracy, the efficiency and the versatility.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge