Few-Shot Learning of Accurate Folding Landscape for Protein Structure Prediction

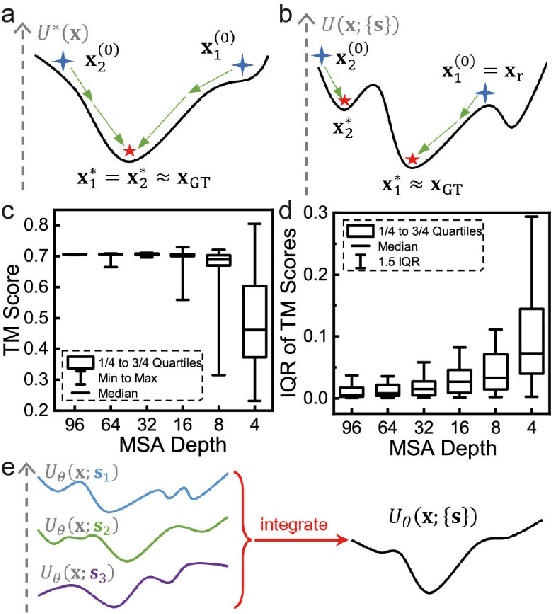
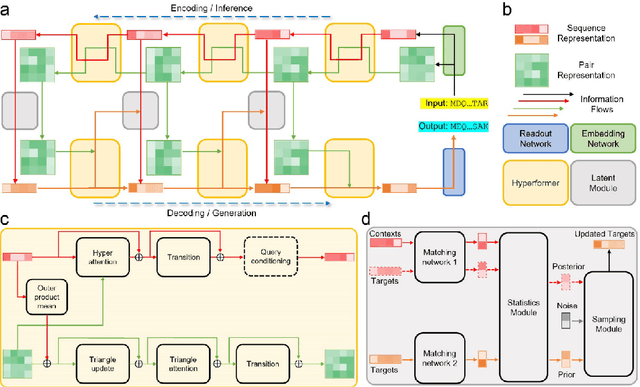
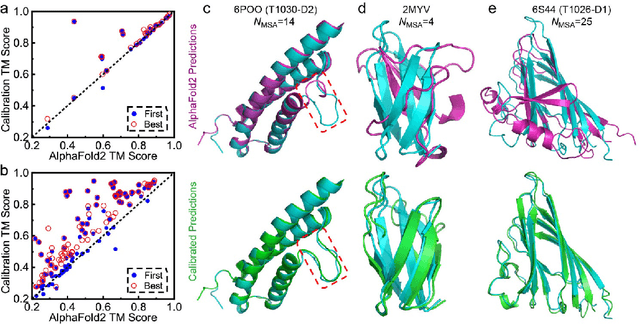
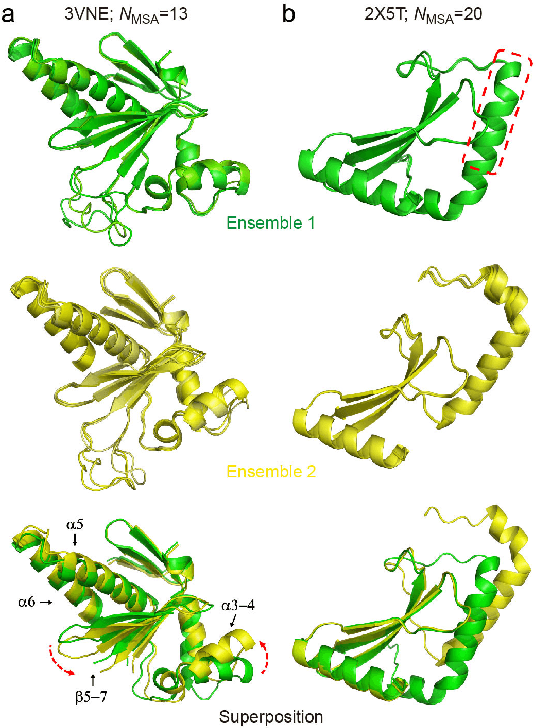
Data-driven predictive methods which can efficiently and accurately transform protein sequences into biologically active structures are highly valuable for scientific research and therapeutical development. Determining accurate folding landscape using co-evolutionary information is fundamental to the success of modern protein structure prediction methods. As the state of the art, AlphaFold2 has dramatically raised the accuracy without performing explicit co-evolutionary analysis. Nevertheless, its performance still shows strong dependence on available sequence homologs. We investigated the cause of such dependence and presented EvoGen, a meta generative model, to remedy the underperformance of AlphaFold2 for poor MSA targets. EvoGen allows us to manipulate the folding landscape either by denoising the searched MSA or by generating virtual MSA, and helps AlphaFold2 fold accurately in low-data regime or even achieve encouraging performance with single-sequence predictions. Being able to make accurate predictions with few-shot MSA not only generalizes AlphaFold2 better for orphan sequences, but also democratizes its use for high-throughput applications. Besides, EvoGen combined with AlphaFold2 yields a probabilistic structure generation method which could explore alternative conformations of protein sequences, and the task-aware differentiable algorithm for sequence generation will benefit other related tasks including protein design.

PSP: Million-level Protein Sequence Dataset for Protein Structure Prediction

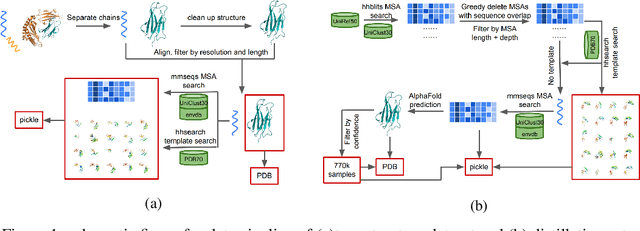
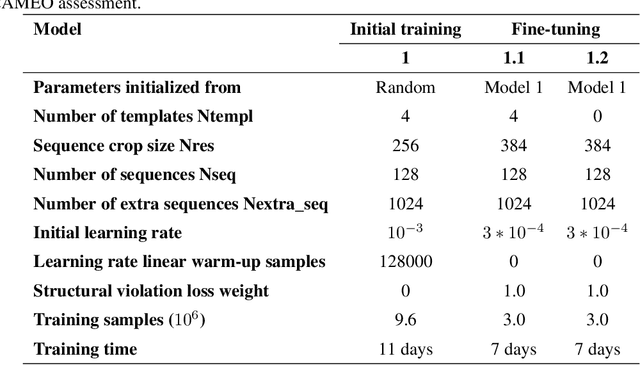
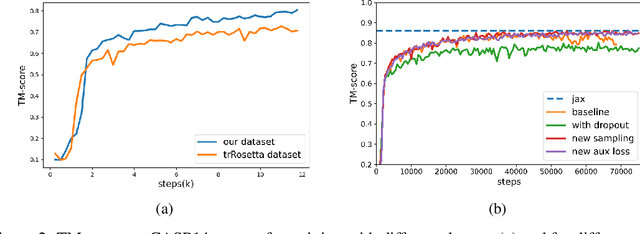
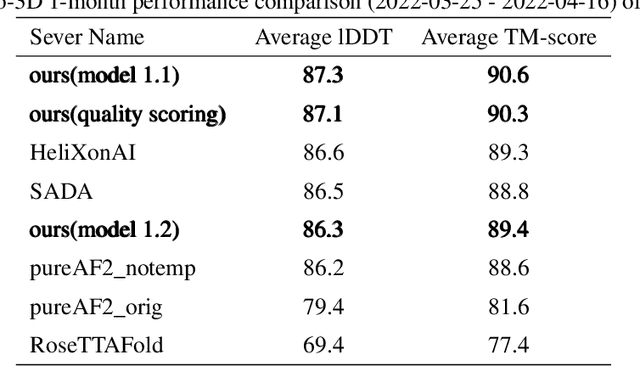
Proteins are essential component of human life and their structures are important for function and mechanism analysis. Recent work has shown the potential of AI-driven methods for protein structure prediction. However, the development of new models is restricted by the lack of dataset and benchmark training procedure. To the best of our knowledge, the existing open source datasets are far less to satisfy the needs of modern protein sequence-structure related research. To solve this problem, we present the first million-level protein structure prediction dataset with high coverage and diversity, named as PSP. This dataset consists of 570k true structure sequences (10TB) and 745k complementary distillation sequences (15TB). We provide in addition the benchmark training procedure for SOTA protein structure prediction model on this dataset. We validate the utility of this dataset for training by participating CAMEO contest in which our model won the first place. We hope our PSP dataset together with the training benchmark can enable a broader community of AI/biology researchers for AI-driven protein related research.

Meta-Auto-Decoder for Solving Parametric Partial Differential Equations

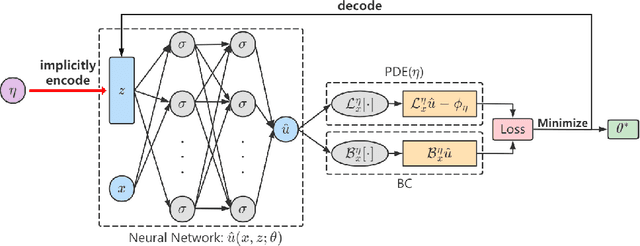
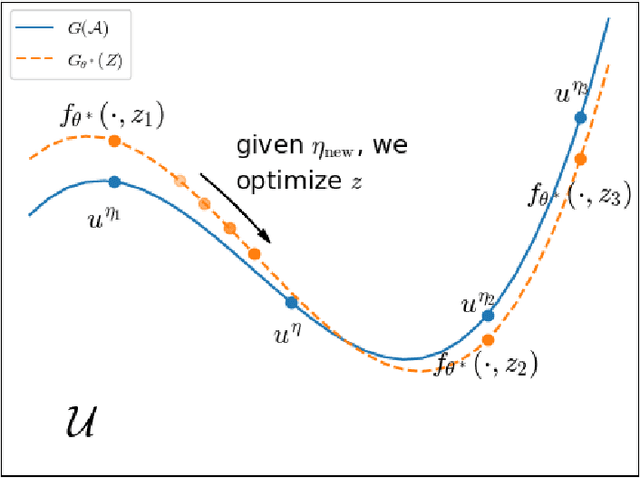
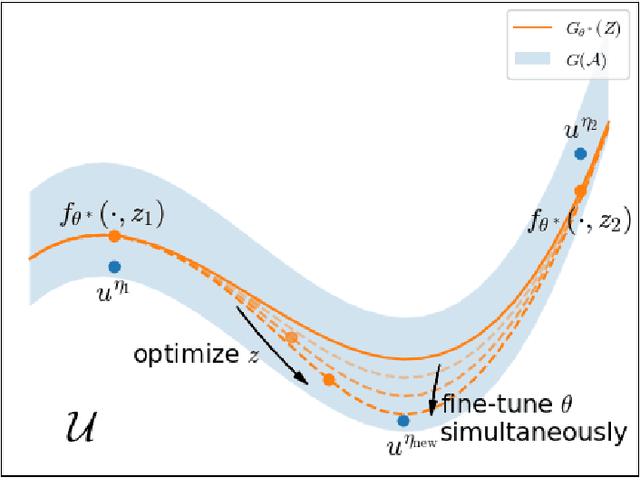
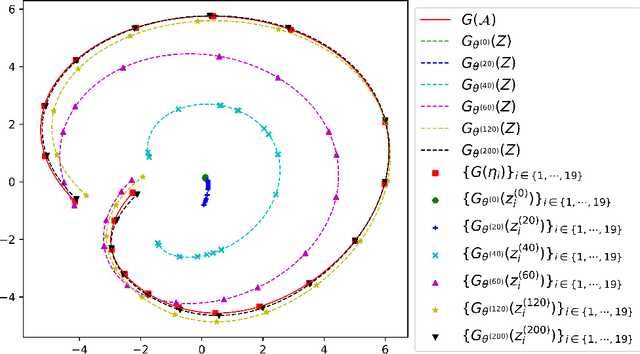
Partial Differential Equations (PDEs) are ubiquitous in many disciplines of science and engineering and notoriously difficult to solve. In general, closed-form solutions of PDEs are unavailable and numerical approximation methods are computationally expensive. The parameters of PDEs are variable in many applications, such as inverse problems, control and optimization, risk assessment, and uncertainty quantification. In these applications, our goal is to solve parametric PDEs rather than one instance of them. Our proposed approach, called Meta-Auto-Decoder (MAD), treats solving parametric PDEs as a meta-learning problem and utilizes the Auto-Decoder structure in \cite{park2019deepsdf} to deal with different tasks/PDEs. Physics-informed losses induced from the PDE governing equations and boundary conditions is used as the training losses for different tasks. The goal of MAD is to learn a good model initialization that can generalize across different tasks, and eventually enables the unseen task to be learned faster. The inspiration of MAD comes from (conjectured) low-dimensional structure of parametric PDE solutions and we explain our approach from the perspective of manifold learning. Finally, we demonstrate the power of MAD though extensive numerical studies, including Burgers' equation, Laplace's equation and time-domain Maxwell's equations. MAD exhibits faster convergence speed without losing the accuracy compared with other deep learning methods.

Solving Partial Differential Equations with Point Source Based on Physics-Informed Neural Networks

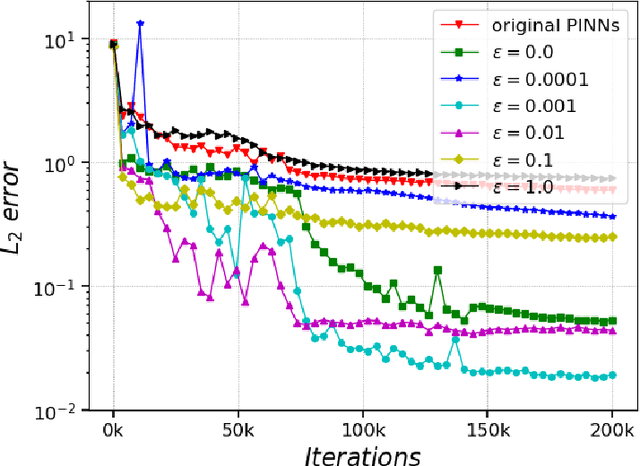
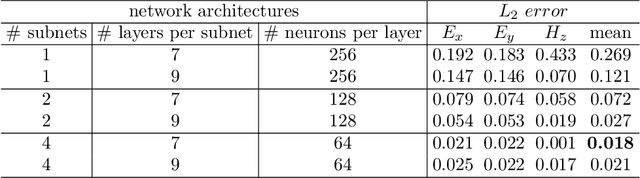
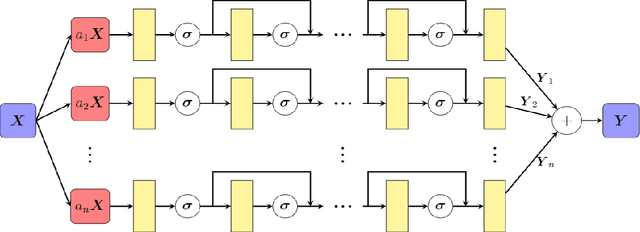
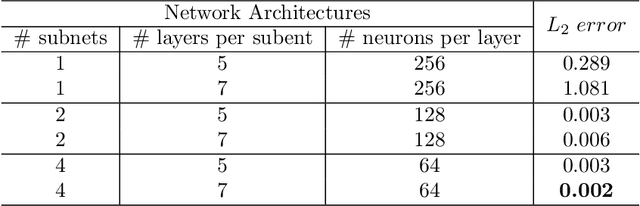
In recent years, deep learning technology has been used to solve partial differential equations (PDEs), among which the physics-informed neural networks (PINNs) emerges to be a promising method for solving both forward and inverse PDE problems. PDEs with a point source that is expressed as a Dirac delta function in the governing equations are mathematical models of many physical processes. However, they cannot be solved directly by conventional PINNs method due to the singularity brought by the Dirac delta function. We propose a universal solution to tackle this problem with three novel techniques. Firstly the Dirac delta function is modeled as a continuous probability density function to eliminate the singularity; secondly a lower bound constrained uncertainty weighting algorithm is proposed to balance the PINNs losses between point source area and other areas; and thirdly a multi-scale deep neural network with periodic activation function is used to improve the accuracy and convergence speed of the PINNs method. We evaluate the proposed method with three representative PDEs, and the experimental results show that our method outperforms existing deep learning-based methods with respect to the accuracy, the efficiency and the versatility.