Meta-Auto-Decoder for Solving Parametric Partial Differential Equations
Paper and Code
Nov 15, 2021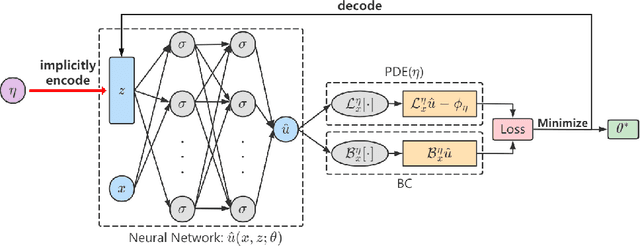
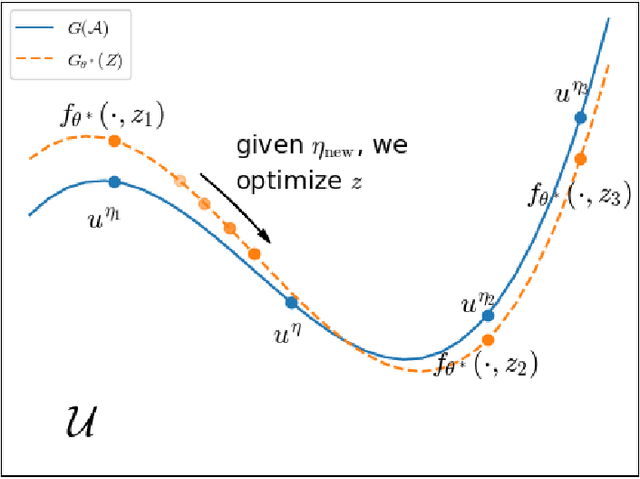
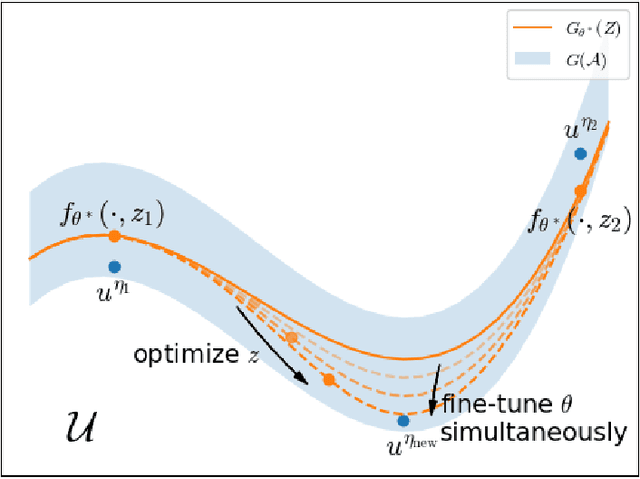
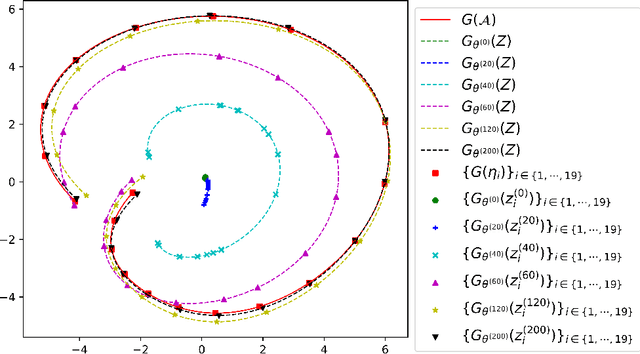
Partial Differential Equations (PDEs) are ubiquitous in many disciplines of science and engineering and notoriously difficult to solve. In general, closed-form solutions of PDEs are unavailable and numerical approximation methods are computationally expensive. The parameters of PDEs are variable in many applications, such as inverse problems, control and optimization, risk assessment, and uncertainty quantification. In these applications, our goal is to solve parametric PDEs rather than one instance of them. Our proposed approach, called Meta-Auto-Decoder (MAD), treats solving parametric PDEs as a meta-learning problem and utilizes the Auto-Decoder structure in \cite{park2019deepsdf} to deal with different tasks/PDEs. Physics-informed losses induced from the PDE governing equations and boundary conditions is used as the training losses for different tasks. The goal of MAD is to learn a good model initialization that can generalize across different tasks, and eventually enables the unseen task to be learned faster. The inspiration of MAD comes from (conjectured) low-dimensional structure of parametric PDE solutions and we explain our approach from the perspective of manifold learning. Finally, we demonstrate the power of MAD though extensive numerical studies, including Burgers' equation, Laplace's equation and time-domain Maxwell's equations. MAD exhibits faster convergence speed without losing the accuracy compared with other deep learning methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge