MSGField: A Unified Scene Representation Integrating Motion, Semantics, and Geometry for Robotic Manipulation

Combining accurate geometry with rich semantics has been proven to be highly effective for language-guided robotic manipulation. Existing methods for dynamic scenes either fail to update in real-time or rely on additional depth sensors for simple scene editing, limiting their applicability in real-world. In this paper, we introduce MSGField, a representation that uses a collection of 2D Gaussians for high-quality reconstruction, further enhanced with attributes to encode semantic and motion information. Specially, we represent the motion field compactly by decomposing each primitive's motion into a combination of a limited set of motion bases. Leveraging the differentiable real-time rendering of Gaussian splatting, we can quickly optimize object motion, even for complex non-rigid motions, with image supervision from only two camera views. Additionally, we designed a pipeline that utilizes object priors to efficiently obtain well-defined semantics. In our challenging dataset, which includes flexible and extremely small objects, our method achieve a success rate of 79.2% in static and 63.3% in dynamic environments for language-guided manipulation. For specified object grasping, we achieve a success rate of 90%, on par with point cloud-based methods. Code and dataset will be released at:https://shengyu724.github.io/MSGField.github.io.

Learning to simulate partially known spatio-temporal dynamics with trainable difference operators

Recently, using neural networks to simulate spatio-temporal dynamics has received a lot of attention. However, most existing methods adopt pure data-driven black-box models, which have limited accuracy and interpretability. By combining trainable difference operators with black-box models, we propose a new hybrid architecture explicitly embedded with partial prior knowledge of the underlying PDEs named PDE-Net++. Furthermore, we introduce two distinct options called the trainable flipping difference layer (TFDL) and the trainable dynamic difference layer (TDDL) for the difference operators. Numerous numerical experiments have demonstrated that PDE-Net++ has superior prediction accuracy and better extrapolation performance than black-box models.

Meta-Auto-Decoder for Solving Parametric Partial Differential Equations

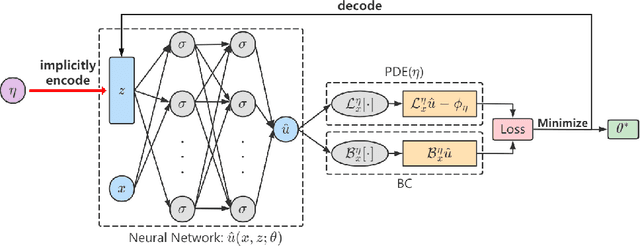
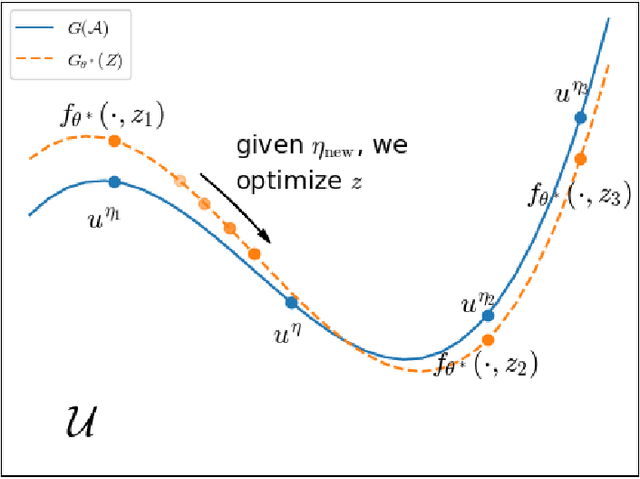
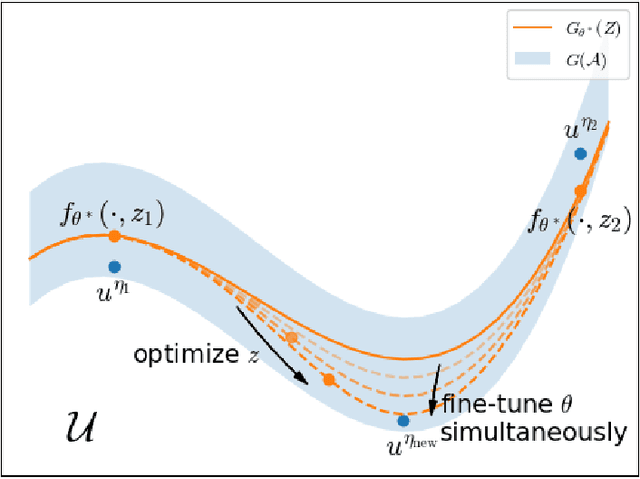
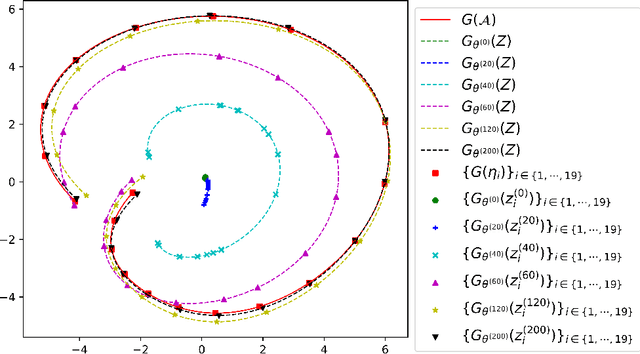
Partial Differential Equations (PDEs) are ubiquitous in many disciplines of science and engineering and notoriously difficult to solve. In general, closed-form solutions of PDEs are unavailable and numerical approximation methods are computationally expensive. The parameters of PDEs are variable in many applications, such as inverse problems, control and optimization, risk assessment, and uncertainty quantification. In these applications, our goal is to solve parametric PDEs rather than one instance of them. Our proposed approach, called Meta-Auto-Decoder (MAD), treats solving parametric PDEs as a meta-learning problem and utilizes the Auto-Decoder structure in \cite{park2019deepsdf} to deal with different tasks/PDEs. Physics-informed losses induced from the PDE governing equations and boundary conditions is used as the training losses for different tasks. The goal of MAD is to learn a good model initialization that can generalize across different tasks, and eventually enables the unseen task to be learned faster. The inspiration of MAD comes from (conjectured) low-dimensional structure of parametric PDE solutions and we explain our approach from the perspective of manifold learning. Finally, we demonstrate the power of MAD though extensive numerical studies, including Burgers' equation, Laplace's equation and time-domain Maxwell's equations. MAD exhibits faster convergence speed without losing the accuracy compared with other deep learning methods.

Solving Partial Differential Equations with Point Source Based on Physics-Informed Neural Networks

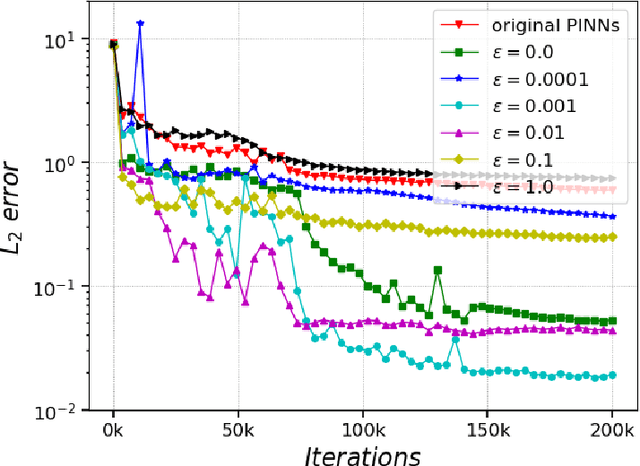
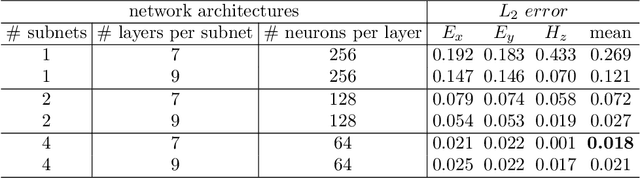
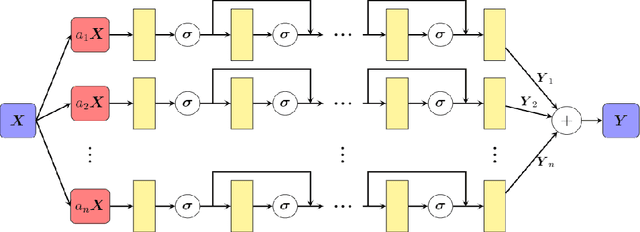
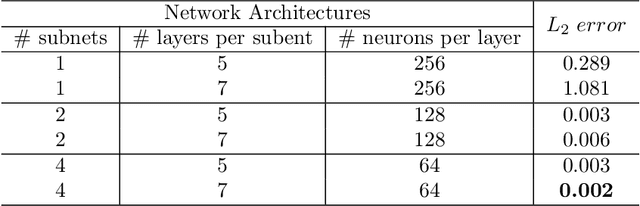
In recent years, deep learning technology has been used to solve partial differential equations (PDEs), among which the physics-informed neural networks (PINNs) emerges to be a promising method for solving both forward and inverse PDE problems. PDEs with a point source that is expressed as a Dirac delta function in the governing equations are mathematical models of many physical processes. However, they cannot be solved directly by conventional PINNs method due to the singularity brought by the Dirac delta function. We propose a universal solution to tackle this problem with three novel techniques. Firstly the Dirac delta function is modeled as a continuous probability density function to eliminate the singularity; secondly a lower bound constrained uncertainty weighting algorithm is proposed to balance the PINNs losses between point source area and other areas; and thirdly a multi-scale deep neural network with periodic activation function is used to improve the accuracy and convergence speed of the PINNs method. We evaluate the proposed method with three representative PDEs, and the experimental results show that our method outperforms existing deep learning-based methods with respect to the accuracy, the efficiency and the versatility.