Predicting parametric spatiotemporal dynamics by multi-resolution PDE structure-preserved deep learning
Paper and Code
May 09, 2022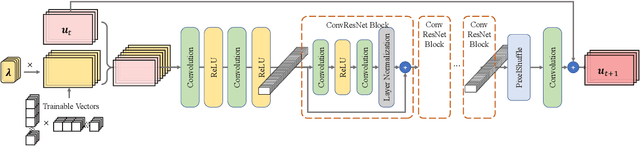
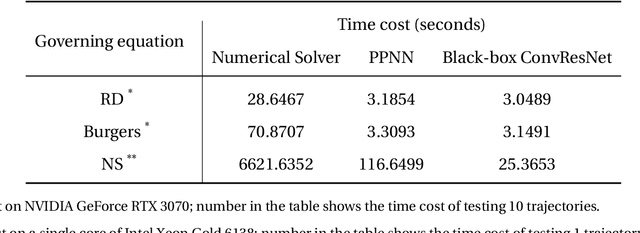
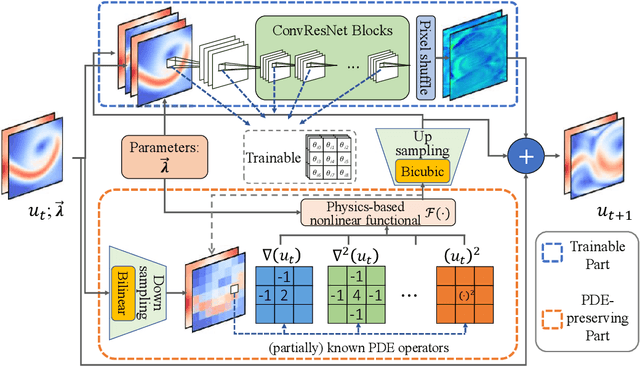
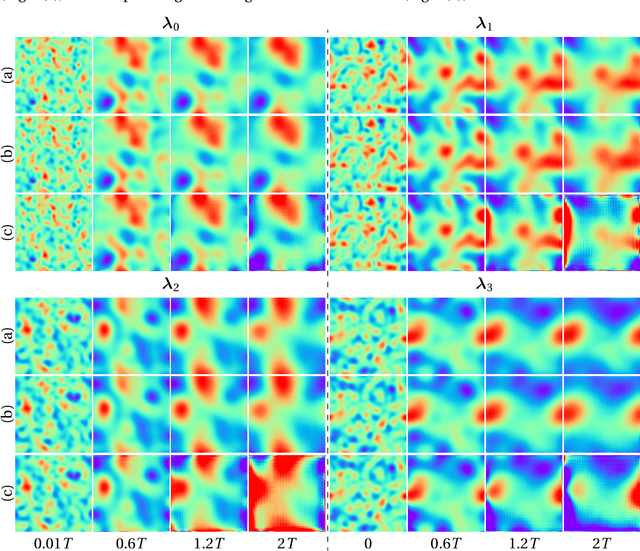
Although recent advances in deep learning (DL) have shown a great promise for learning physics exhibiting complex spatiotemporal dynamics, the high training cost, unsatisfying extrapolability for long-term predictions, and poor generalizability in out-of-sample regimes significantly limit their applications in science/engineering problems. A more promising way is to leverage available physical prior and domain knowledge to develop scientific DL models, known as physics-informed deep learning (PiDL). In most existing PiDL frameworks, e.g., physics-informed neural networks, the physics prior is mainly utilized to regularize neural network training by incorporating governing equations into the loss function in a soft manner. In this work, we propose a new direction to leverage physics prior knowledge by baking the mathematical structures of governing equations into the neural network architecture design. In particular, we develop a novel PDE-preserved neural network (PPNN) for rapidly predicting parametric spatiotemporal dynamics, given the governing PDEs are (partially) known. The discretized PDE structures are preserved in PPNN as convolutional residual network (ConvResNet) blocks, which are formulated in a multi-resolution setting. This physics-inspired learning architecture design endows PPNN with excellent generalizability and long-term prediction accuracy compared to the state-of-the-art black-box ConvResNet baseline. The effectiveness and merit of the proposed methods have been demonstrated over a handful of spatiotemporal dynamical systems governed by unsteady PDEs, including reaction-diffusion, Burgers', and Navier-Stokes equations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge