Omri Azencot
Ben Gurion University of the Negev
Bridging Efficiency and Safety: Formal Verification of Neural Networks with Early Exits
Dec 23, 2025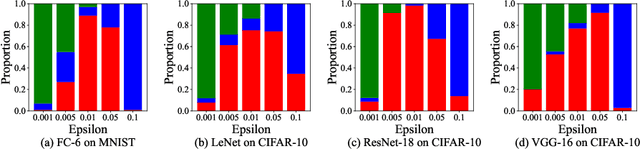
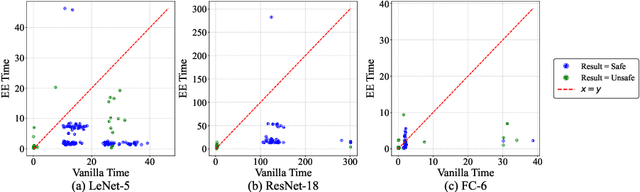


Abstract:Ensuring the safety and efficiency of AI systems is a central goal of modern research. Formal verification provides guarantees of neural network robustness, while early exits improve inference efficiency by enabling intermediate predictions. Yet verifying networks with early exits introduces new challenges due to their conditional execution paths. In this work, we define a robustness property tailored to early exit architectures and show how off-the-shelf solvers can be used to assess it. We present a baseline algorithm, enhanced with an early stopping strategy and heuristic optimizations that maintain soundness and completeness. Experiments on multiple benchmarks validate our framework's effectiveness and demonstrate the performance gains of the improved algorithm. Alongside the natural inference acceleration provided by early exits, we show that they also enhance verifiability, enabling more queries to be solved in less time compared to standard networks. Together with a robustness analysis, we show how these metrics can help users navigate the inherent trade-off between accuracy and efficiency.
Towards General Modality Translation with Contrastive and Predictive Latent Diffusion Bridge
Oct 23, 2025

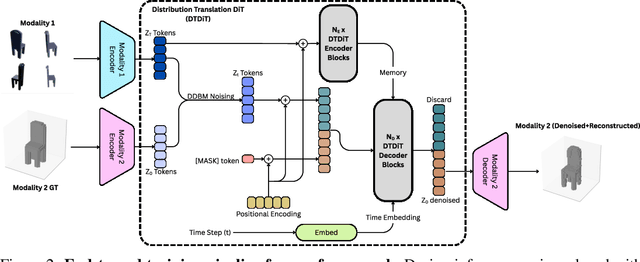

Abstract:Recent advances in generative modeling have positioned diffusion models as state-of-the-art tools for sampling from complex data distributions. While these models have shown remarkable success across single-modality domains such as images and audio, extending their capabilities to Modality Translation (MT), translating information across different sensory modalities, remains an open challenge. Existing approaches often rely on restrictive assumptions, including shared dimensionality, Gaussian source priors, and modality-specific architectures, which limit their generality and theoretical grounding. In this work, we propose the Latent Denoising Diffusion Bridge Model (LDDBM), a general-purpose framework for modality translation based on a latent-variable extension of Denoising Diffusion Bridge Models. By operating in a shared latent space, our method learns a bridge between arbitrary modalities without requiring aligned dimensions. We introduce a contrastive alignment loss to enforce semantic consistency between paired samples and design a domain-agnostic encoder-decoder architecture tailored for noise prediction in latent space. Additionally, we propose a predictive loss to guide training toward accurate cross-domain translation and explore several training strategies to improve stability. Our approach supports arbitrary modality pairs and performs strongly on diverse MT tasks, including multi-view to 3D shape generation, image super-resolution, and multi-view scene synthesis. Comprehensive experiments and ablations validate the effectiveness of our framework, establishing a new strong baseline in general modality translation. For more information, see our project page: https://sites.google.com/view/lddbm/home.
Super-Linear: A Lightweight Pretrained Mixture of Linear Experts for Time Series Forecasting
Sep 18, 2025Abstract:Time series forecasting (TSF) is critical in domains like energy, finance, healthcare, and logistics, requiring models that generalize across diverse datasets. Large pre-trained models such as Chronos and Time-MoE show strong zero-shot (ZS) performance but suffer from high computational costs. In this work, We introduce Super-Linear, a lightweight and scalable mixture-of-experts (MoE) model for general forecasting. It replaces deep architectures with simple frequency-specialized linear experts, trained on resampled data across multiple frequency regimes. A lightweight spectral gating mechanism dynamically selects relevant experts, enabling efficient, accurate forecasting. Despite its simplicity, Super-Linear matches state-of-the-art performance while offering superior efficiency, robustness to various sampling rates, and enhanced interpretability. The implementation of Super-Linear is available at \href{https://github.com/azencot-group/SuperLinear}{https://github.com/azencot-group/SuperLinear}
Unraveling Hidden Representations: A Multi-Modal Layer Analysis for Better Synthetic Content Forensics
Aug 01, 2025Abstract:Generative models achieve remarkable results in multiple data domains, including images and texts, among other examples. Unfortunately, malicious users exploit synthetic media for spreading misinformation and disseminating deepfakes. Consequently, the need for robust and stable fake detectors is pressing, especially when new generative models appear everyday. While the majority of existing work train classifiers that discriminate between real and fake information, such tools typically generalize only within the same family of generators and data modalities, yielding poor results on other generative classes and data domains. Towards a universal classifier, we propose the use of large pre-trained multi-modal models for the detection of generative content. Effectively, we show that the latent code of these models naturally captures information discriminating real from fake. Building on this observation, we demonstrate that linear classifiers trained on these features can achieve state-of-the-art results across various modalities, while remaining computationally efficient, fast to train, and effective even in few-shot settings. Our work primarily focuses on fake detection in audio and images, achieving performance that surpasses or matches that of strong baseline methods.
Curvature Enhanced Data Augmentation for Regression
Jun 07, 2025Abstract:Deep learning models with a large number of parameters, often referred to as over-parameterized models, have achieved exceptional performance across various tasks. Despite concerns about overfitting, these models frequently generalize well to unseen data, thanks to effective regularization techniques, with data augmentation being among the most widely used. While data augmentation has shown great success in classification tasks using label-preserving transformations, its application in regression problems has received less attention. Recently, a novel \emph{manifold learning} approach for generating synthetic data was proposed, utilizing a first-order approximation of the data manifold. Building on this foundation, we present a theoretical framework and practical tools for approximating and sampling general data manifolds. Furthermore, we introduce the Curvature-Enhanced Manifold Sampling (CEMS) method for regression tasks. CEMS leverages a second-order representation of the data manifold to enable efficient sampling and reconstruction of new data points. Extensive evaluations across multiple datasets and comparisons with state-of-the-art methods demonstrate that CEMS delivers superior performance in both in-distribution and out-of-distribution scenarios, while introducing only minimal computational overhead. Code is available at https://github.com/azencot-group/CEMS.
Time Series Generation Under Data Scarcity: A Unified Generative Modeling Approach
May 26, 2025Abstract:Generative modeling of time series is a central challenge in time series analysis, particularly under data-scarce conditions. Despite recent advances in generative modeling, a comprehensive understanding of how state-of-the-art generative models perform under limited supervision remains lacking. In this work, we conduct the first large-scale study evaluating leading generative models in data-scarce settings, revealing a substantial performance gap between full-data and data-scarce regimes. To close this gap, we propose a unified diffusion-based generative framework that can synthesize high-fidelity time series across diverse domains using just a few examples. Our model is pre-trained on a large, heterogeneous collection of time series datasets, enabling it to learn generalizable temporal representations. It further incorporates architectural innovations such as dynamic convolutional layers for flexible channel adaptation and dataset token conditioning for domain-aware generation. Without requiring abundant supervision, our unified model achieves state-of-the-art performance in few-shot settings-outperforming domain-specific baselines across a wide range of subset sizes. Remarkably, it also surpasses all baselines even when tested on full datasets benchmarks, highlighting the strength of pre-training and cross-domain generalization. We hope this work encourages the community to revisit few-shot generative modeling as a key problem in time series research and pursue unified solutions that scale efficiently across domains. Code is available at https://github.com/azencot-group/ImagenFew.
FLEX: A Backbone for Diffusion-Based Modeling of Spatio-temporal Physical Systems
May 23, 2025Abstract:We introduce FLEX (FLow EXpert), a backbone architecture for generative modeling of spatio-temporal physical systems using diffusion models. FLEX operates in the residual space rather than on raw data, a modeling choice that we motivate theoretically, showing that it reduces the variance of the velocity field in the diffusion model, which helps stabilize training. FLEX integrates a latent Transformer into a U-Net with standard convolutional ResNet layers and incorporates a redesigned skip connection scheme. This hybrid design enables the model to capture both local spatial detail and long-range dependencies in latent space. To improve spatio-temporal conditioning, FLEX uses a task-specific encoder that processes auxiliary inputs such as coarse or past snapshots. Weak conditioning is applied to the shared encoder via skip connections to promote generalization, while strong conditioning is applied to the decoder through both skip and bottleneck features to ensure reconstruction fidelity. FLEX achieves accurate predictions for super-resolution and forecasting tasks using as few as two reverse diffusion steps. It also produces calibrated uncertainty estimates through sampling. Evaluations on high-resolution 2D turbulence data show that FLEX outperforms strong baselines and generalizes to out-of-distribution settings, including unseen Reynolds numbers, physical observables (e.g., fluid flow velocity fields), and boundary conditions.
One-Step Offline Distillation of Diffusion-based Models via Koopman Modeling
May 19, 2025Abstract:Diffusion-based generative models have demonstrated exceptional performance, yet their iterative sampling procedures remain computationally expensive. A prominent strategy to mitigate this cost is distillation, with offline distillation offering particular advantages in terms of efficiency, modularity, and flexibility. In this work, we identify two key observations that motivate a principled distillation framework: (1) while diffusion models have been viewed through the lens of dynamical systems theory, powerful and underexplored tools can be further leveraged; and (2) diffusion models inherently impose structured, semantically coherent trajectories in latent space. Building on these observations, we introduce the Koopman Distillation Model KDM, a novel offline distillation approach grounded in Koopman theory-a classical framework for representing nonlinear dynamics linearly in a transformed space. KDM encodes noisy inputs into an embedded space where a learned linear operator propagates them forward, followed by a decoder that reconstructs clean samples. This enables single-step generation while preserving semantic fidelity. We provide theoretical justification for our approach: (1) under mild assumptions, the learned diffusion dynamics admit a finite-dimensional Koopman representation; and (2) proximity in the Koopman latent space correlates with semantic similarity in the generated outputs, allowing for effective trajectory alignment. Empirically, KDM achieves state-of-the-art performance across standard offline distillation benchmarks, improving FID scores by up to 40% in a single generation step. All implementation details and code for the experimental setups are provided in our GitHub - https://github.com/azencot-group/KDM, or in our project page - https://sites.google.com/view/koopman-distillation-model.
A Multi-Task Learning Approach to Linear Multivariate Forecasting
Feb 05, 2025



Abstract:Accurate forecasting of multivariate time series data is important in many engineering and scientific applications. Recent state-of-the-art works ignore the inter-relations between variates, using their model on each variate independently. This raises several research questions related to proper modeling of multivariate data. In this work, we propose to view multivariate forecasting as a multi-task learning problem, facilitating the analysis of forecasting by considering the angle between task gradients and their balance. To do so, we analyze linear models to characterize the behavior of tasks. Our analysis suggests that tasks can be defined by grouping similar variates together, which we achieve via a simple clustering that depends on correlation-based similarities. Moreover, to balance tasks, we scale gradients with respect to their prediction error. Then, each task is solved with a linear model within our MTLinear framework. We evaluate our approach on challenging benchmarks in comparison to strong baselines, and we show it obtains on-par or better results on multivariate forecasting problems. The implementation is available at: https://github.com/azencot-group/MTLinear
Beyond Data Scarcity: A Frequency-Driven Framework for Zero-Shot Forecasting
Nov 24, 2024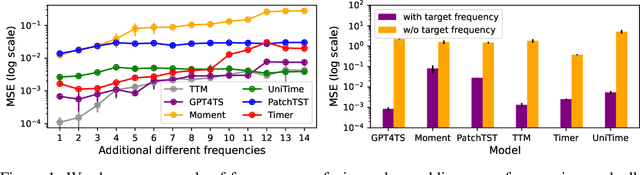
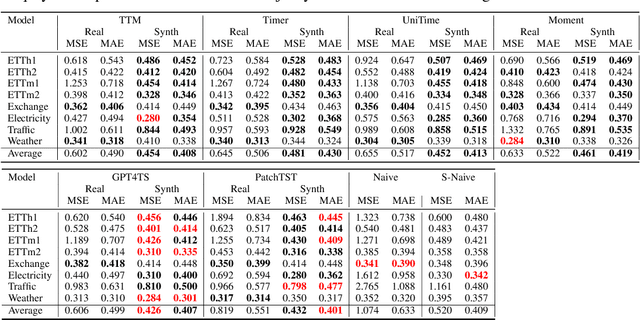
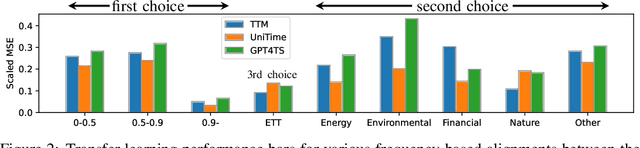
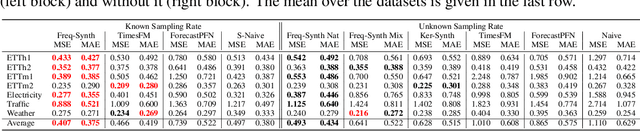
Abstract:Time series forecasting is critical in numerous real-world applications, requiring accurate predictions of future values based on observed patterns. While traditional forecasting techniques work well in in-domain scenarios with ample data, they struggle when data is scarce or not available at all, motivating the emergence of zero-shot and few-shot learning settings. Recent advancements often leverage large-scale foundation models for such tasks, but these methods require extensive data and compute resources, and their performance may be hindered by ineffective learning from the available training set. This raises a fundamental question: What factors influence effective learning from data in time series forecasting? Toward addressing this, we propose using Fourier analysis to investigate how models learn from synthetic and real-world time series data. Our findings reveal that forecasters commonly suffer from poor learning from data with multiple frequencies and poor generalization to unseen frequencies, which impedes their predictive performance. To alleviate these issues, we present a novel synthetic data generation framework, designed to enhance real data or replace it completely by creating task-specific frequency information, requiring only the sampling rate of the target data. Our approach, Freq-Synth, improves the robustness of both foundation as well as nonfoundation forecast models in zero-shot and few-shot settings, facilitating more reliable time series forecasting under limited data scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge